Analiticheskaya_Geometria

ляющие косинусы n = {cosα, cos β, cosγ}. Если M(x, y, z) − произвольная точка плоскости π , проекция вектора OM на нормаль OP равна p , т. е.:

прOP OM = прn OM = p .	(3.7)
Учитывая, что OM = {x, y, z}, прn OM = OM n , получим:
прn OM = xcosα + ycos β + zcosγ .	(3.8)
Из соотношений (3.7) и (3.8) следует нормальное уравнение плос-
кости:
xcosα + ycos β + zcosγ − p = 0 .	(3.9)
Теорема 3. Если точка M1 имеет координаты (x1, y1, z1)	и плоскость π

задана нормальным уравнением xcosα + ycos β + zcosγ = p , то расстояние d от точки M1 до плоскости π определяется по формуле

d =		x1 cosα + y1 cos β + z1 cosγ − p		.	(3.10)
Доказательство. Пусть Q − проекция точки M1					на направленную
нормаль. Тогда в силу основного алгебраического тождества OQ = OP + PQ

или PQ = OQ −OP , откуда следует, что d = PQ = OQ −OP . Но OQ = прn OM1 ,

OP = p ,

т. е. d =

прn OM1 − p

. Вектор OM1

имеет координаты {x1, y1, z1} и

прn OM1

= n OM1 = x1 cosα − y1 cos β − z1 cosγ .

Поэтому

d =

PQ

=

OQ −OP

=

= x1 cosα + y1 cos β + z1 cosγ − p . Теорема доказана.

Пусть уравнения Ax + By +Cz + D = 0 и xcosα + ycos β + zcosγ − p = 0 яв-

ляются общим и нормальным уравнениями одной и той же плоскости π . По теореме 2 коэффициенты в этих уравнениях пропорциональны, т. е.

cosα = µA, cos β = µB , cosγ = µC .					Так как cos2 α + cos2 β + cos2 γ = =1, то
µ2 (A2 + B2 +C2 ) =1 или µ = ±			1					.
		2		2	+C	2
		A + B
Определение. Число µ , с помощью которого общее уравнение плос-

кости преобразуется к нормальному, называется нормирующим множи-

телем.

Знак числа µ определяется из условия p = −µD , т. е. оно имеет знак,

противоположный знаку свободного члена общего уравнения. Если в уравнении (3.2) D = 0 , то знак нормирующего множителя выбирается про-

извольно.
П р и м е р 31. Найти расстояние d от точки M1(1, 3, 0)	до плоскости
x − 2y − 2z + 7 = 0 .
Решение. Прежде всего нужно общее уравнение плоскости привести
к нормальному виду. Найдем нормирующий множитель	µ2 (12 + (−2)2 +

+ (−2)2 ) = 9µ2 =1. В общем уравнении плоскости D = 7 0 , поэтому µ 0,

64

т.

е.

µ = −

1 . Следовательно, нормальное уравнение плоскости имеет вид

3

1 x1 +

2 y1 +

2 z1

− 7

− 1 + 2 + 0 −

7

− 2

= 2 .

−

1 x + 2 y +

2 z −

7 = 0 . Тогда d =

−

=

=

3

3

3

3

3

3

3

3

3

3

3

3

Следствие. Если точка M1

имеет координаты (x1, y1, z1) и плоскость π

задана общим уравнением Ax + By +Cz + D = 0 ,

то расстояние d

от точки M1

до плоскости π определяется по формуле

d =

Ax1 + By1 +Cz1 + D

.

(3.11)

A2 + B2 +C2

Доказательство. Направляющие косинусы нормали плоскости связаны с коэффициентами общего уравнения плоскости соотношениями

cosα = µA, cos β = µB , cosγ = µC ,

где

µ = ±

1

− нормирующий

2

+ B

2

+C

2

множитель. Учитывая,

что p = −µD ,

A

преобразуем формулу

(3.10): d =

=

x1 cosα + y1 cos β + z1 cosγ − p

=

x1µA+ y1µB + z1µC + µD

=

µ(x1 A+ y1B + z1C + D)

=

=

µ

x1 A+ y1B + z1C + D

=

1

x1 A+ y1B + z1C + D

=

Ax1 + By1 +Cz1 + D

.

2

+ B

2

+C

2

2

2

+C

2

A

A + B

Следствие доказано.

3.6. Пучки и связки плоскостей

Определение. Совокупность всех плоскостей, проходящих через одну и ту же прямую L, называется пучком плоскостей (с центром в L).

Теорема 4. Если A1x + B1 y +C1z + D1 = 0 и A2 x + B2 y +C2 z + D2 = 0 − урав-

нения двух различных и не параллельных плоскостей, пересечением которых является некоторая прямая L, а α и β − произвольные числа, удовлетворяющие условию α2 + β2 ≠ 0 , то уравнение

α(A1x + B1 y +C1z + D1) + β(A2 x + B2 y +C2 z + D2 ) = 0

(3.12)

определяет плоскость, проходящую через прямую L. Более того, найдутся α и β такие, что любая плоскость, проходящая через прямую L, описыва-

ется уравнением (3.12).

Доказательство. Покажем, что при выполнении условия α2 + β2 ≠ 0

уравнение (3.12) представляет собой уравнение первого порядка. Запишем

(3.12) в виде

(αA1 + βA2 )x + (αB1 + βB2 )y + (αC1 + βC2 )z + (αD1 + βD2 ) = 0 .

(3.13)

Предположим, что в выражении (3.13) все коэффициенты, стоящие

перед переменными, обращаются в нуль,

т.

е. αA1 + βA2 = 0,

αB1 + βB2 = 0 и

αC1 + βC2

= 0 . Так как α2 + β2 ≠ 0 ,

то, положив для определенности α ≠ 0 ,

получим

A1

= −

β

,

B1

= −

β

,

C1 = −

β

, т. е.

A1

=

B1

= C1 . Последнее равенст-

A

α

B

α

C

2

α

A

B

C

2

2

2

2

2

во является условием параллельности плоскостей, задаваемых уравнения-

65

ми A1x + B1 y +C1z + D1 = 0 и A2 x + B2 y +C2 z + D2 = 0 , и противоречит предположению о том, что эти плоскости пересекаются и не совпадают. Таким об-

разом, при условии α2 + β2 ≠ 0 уравнение (3.13) (соответственно и уравне-

ние (3.12)) является уравнением первой степени и, как было показано ранее, определяет некоторую плоскость.

Если M0 (x0 , y0 , z0 ) − произвольная точка линии L пересечения плоскостей, задаваемых уравнениями A1x + B1 y +C1z + D1 = 0 и A2 x + B2 y +C2 z + D2 = 0 ,

то эта точка принадлежит каждой	из этих плоскостей, т. е. выполняются
равенства A1x0 + B1 y0 +C1z0 + D1 = 0 и	A2 x0 + B2 y0 +C2 z0 + D2	= 0 , следовательно,
α(A1x0 + B1 y0 +C1z0 + D1) + β(A2 x0 + B2 y0 +C2 z0 + D2 ) = 0 . Это		равносильно тому,

что плоскость, задаваемая уравнением (3.12), проходит через линию пересечения плоскостей, определяемых уравнениями A1x + B1 y +C1z + D1 = 0 и

A2 x + B2 y +C2 z + D2 = 0 .

Покажем, что найдутся α и β такие, что любая плоскость, проходя-

щая через прямую L, описывается уравнением (3.12). Любая плоскость, проходящая через прямую L, определяется заданием еще одной точки M1(x1, y1, z1) , не принадлежащей прямой L. Если такая плоскость задается

уравнением (3.12), то координаты точки M1(x1, y1, z1) удовлетворяют уравнению

α(A1x1 + B1 y1 +C1z1 + D1) + β(A2 x1 + B2 y1 +C2 z1 + D2 ) = 0 .

(3.14)

Так как точка M1 не принадлежит одновременно двум плоскостям,

задаваемым уравнениями A1x + B1 y +C1z + D1 = 0 и A2 x + B2 y +C2 z + D2 = 0 , то не могут одновременно обратиться в нуль выражения, стоящие в скобках вы-

ражения (3.14). Для определенности будем считать, что

A1x1 + B1 y1 +C1z1 + D1 ≠ 0 . Тогда при β ≠ 0 (если β = 0 и A1x1 + B1 y1 +C1z1 + D1 ≠ 0 ,

то α = 0, что противоречит условию α2 + β2 ≠ 0 ) из уравнения (3.14) можем определить коэффициент α :

α = −

A2 x1 + B2 y1 +C2 z1 + D2

β .

Ax + B y +C z + D

1

1

1

1

1

1

1

При указанных α

и

β

плоскость, определяемая уравнением (3.12),

проходит через точку M1(x1, y1, z1) . Если же

A2 x1 + B2 y1 +C2 z1 + D ≠ 0 , то, рас-

суждая аналогично,

при α ≠ 0 найдем β = −

A1x1 + B1 y1 +C1z1 + D1

α . Теорема

A x + B y +C z

+ D

доказана.

2

1

2

1

2

1

2

β

Учитывая,

что

α2 + β2 ≠ 0 , при α ≠ 0

введем обозначение λ

=

и

α

уравнение (3.12) запишем в виде

(A1x + B1 y +C1z + D1) + λ(A2 x + B2 y +C2 z + D2 ) = 0 .

(3.15)

Уравнение (3.15) содержит все плоскости, проходящие через пря-

мую, определяемую

как

пересечение плоскостей

A1x + B1 y +C1z + D1

= 0

и

A2 x + B2 y +C2 z + D2

= 0 кроме плоскости A1x + B1 y +C1z + D1

= 0 . Поэтому пучок

66

плоскостей может быть задан совокупностью уравнений

A1x + B1 y +C1z + D1 = 0 и (A1x + B1 y +C1z + D1) + λ(A2 x + B2 y +C2 z + D2 ) = 0 .

Доказанная теорема позволяет задавать прямую, являющуюся лини-

ей пересечения	двух	не параллельных и не совпадающих плоскостей
A1x + B1 y +C1z + D1	= 0 и	A2 x + B2 y +C2 z + D2 = 0 , не только двумя уравнениями

этих плоскостей, но и любыми двумя различными уравнениями пучка (3.12), полученными при произвольных значениях α и β .

Определение. Совокупность всех плоскостей, проходящих через

данную точку	M0 (x0 , y0 , z0 ) , называется связкой плоскостей (с центром в
точке M0 ).
Теорема	5. Уравнение связки плоскостей	с центром в точке
M0 (x0 , y0 , z0 ) имеет вид
	A(x − x0 ) + B(y − y0 ) +C(z − z0 ) = 0 ,	(3.16)

где A, B, C − произвольные числа, не равные одновременно нулю, т. е. они

должны удовлетворять условию A2 + B2 +C2 ≠ 0 .

Доказательство. Очевидно, что любая плоскость, задаваемая уравнением (3.16), проходит через точку M0 (x0 , y0 , z0 ) . Если же π является за-

данной плоскостью, проходящей через точку M0 (x0 , y0 , z0 ) , то эта плоскость однозначно определяется заданием еще и нормального вектора N = {A, B, C}. Таким образом, плоскость задается уравнением (3.1), совпадающим с уравнением (3.16). Теорема доказана.

3.7. Уравнения прямой в пространстве

Любую линию в пространстве можно рассматривать как пересечение двух поверхностей и задавать ее системой двух уравнений. Поэтому любую прямую можно рассматривать как линию пересечения плоскостей и определять заданием двух уравнений первой степени.

Пусть задана некоторая прямоугольная система координат Oxyz и прямая L. Пусть π1 и π2 − две различные плоскости, пересекающиеся по прямой L и задаваемые соответственно уравнениями A1x + B1 y +C1z + D1 = 0 и A2 x + B2 y +C2 z + D2 = 0 . Эти два уравнения совместно определяют прямую L в том и только в том случае, когда они не параллельны и не совпадают

друг с другом, т. е. нормальные векторы N1 = {A1, B1,C1} и N2	= {A2 , B2 ,C2} этих
плоскостей не коллинеарны.
Определение. Если коэффициенты уравнений
A1x + B1 y +C1z + D1 = 0 и A2 x + B2 y +C2 z + D2 = 0	(3.17)

не пропорциональны, то эти уравнения называются общими уравнениями прямой, определяемой как линия пересечения плоскостей.

Определение. Любой ненулевой вектор, параллельный прямой, на-

зывается направляющим вектором этой прямой.

67

Выведем уравнение прямой L, проходящей через данную точку M0 (x0 , y0 , z0 ) пространства и имеющей заданный направляющий вектор

a = {l, m, n}.

Пусть точка M(x, y, z)

− произвольная точка прямой L. Эта точка ле-

жит на прямой тогда и только тогда, когда вектор M0M , имеющий коорди-

наты

{x − x0 , y − y0 , z − z0}, коллинеарен направляющему вектору

a = {l, m, n}

прямой. Согласно (2.28) условие коллинеарности векторов M0M и a

имеет

вид

x − x0

y − y0

z − z0

=

=

.

(3.18)

l

m

n

Уравнения (3.18) называются каноническими уравнениями пря-

мой,

проходящей через точку M0 (x0 , y0 , z0 ) и имеющей направляющий век-

тор a = {l, m, n}.

Если прямая L задана общими уравнениями (3.17), то направляющий

вектор a

этой прямой ортогонален нормальным векторам

N1

= {A1, B1,C1} и

N2 = {A2 , B2 ,C2} плоскостей, задаваемых уравнениями

A1x + B1 y +C1z + D1 = 0 и

A2 x + B2 y +C2 z + D2

= 0 . Вектор N1 × N2 по свойству векторного произведения

ортогонален каждому из векторов N1

и N2 . Согласно определению в каче-

стве направляющего вектора a

прямой L можно взять вектор N1 × N2 ,

т. е.

B C

,

C A

,

A B

a

=

1

1

1

1

1

1

.

B2 C2

C2 A2

A2 B2

Для нахождения точки M0 (x0 , y0 , z0 ) рассмотрим систему уравнений

Ax + B y

+C z + D

= 0

.

Так

как плоскости, определяемые

уравнениями

1

1

1

1

A2 x + B2 y +C2 z + D2 = 0

A1x + B1 y +C1z + D1 = 0

и

A2 x + B2 y +C2 z + D2 = 0 , не параллельны и не совпада-

ют, то не выполняется хотя бы одно из равенств

A1

=

B1

= C1

. Это приво-

A

B

C

2

2

2

дит к тому, что хотя бы один из определителей

B1 C1

,

C1

A1

A1

B1

от-

,

B C

2

C

2

A

A B

2

2

2

2

личен от нуля. Для определенности будем считать, что

B1

C1

≠ 0 . Тогда,

B C

2

2

взяв произвольное значение x0 ,

получим систему уравнений относительно

неизвестных y0

и z0 :

B y

+C z

= −(D

+ Ax )

.

1

0

1

0

1

1

0

B2 y0 +C2 z0 = −(D2 + A2 x0 )

По теореме Крамера эта система имеет единственное решение, определяемое формулами

68

y0

=

C1(D2 + A2 x0 ) −C2 (D1 + A1x0 ) ,

z0

= B2 (D1 + A1x0 ) − B1(D2 + A2 x0 ) .

(3.19)

B1C2 − B2C1

B1C2 − B2C1

Если взять x0

= 0 , то прямая, задаваемая уравнениями (3.17), прохо-

дит через точку M0

0, C1D2

−C2D1 ,

B2D1

− B1D2

.

BC

2

− B C BC

2

− B C

1

2

1

1

2

1

Таким образом, для случая, когда

B1

C1

≠ 0

, канонические уравнения

B C

2

2

прямой (3.17) имеют вид

x

y − C1D2 −C2D1

z −

B2D1 − B1D2

B1C2 − B2C1

=

B1C2 − B2C1

=

.

BC

− B C

2

C A −C

A

AB − A B

1

2

1

1

2

2

1

1

2

2

1

Аналогично записываются канонические уравнения прямой (3.17)

для случая, когда отличен от нуля определитель

C1

A1

или

A1 B1

.

C

2

A

A B

2

2

2

Если

прямая

проходит

через

две

различные

точки

M1(x1, y1, z1)

и

M2 (x2 , y2 , z2 ) , то ее канонические уравнения имеют вид

x − x1

=

y − y1

=

z − z1

.

(3.20)

x

− x

y

− y

z − z

2

1

2

1

2

1

Это следует из того, что прямая проходит через точку M1(x1, y1, z1)

и

имеет направляющий вектор a = M1M2 = {x2 − x1, y2 − y1, z2 − z1}.

Рассмотрим канонические уравнения (3.18) прямой. Примем каждое из отношений за параметр t , т. е. x −l x0 = y −my0 = z −nz0 = t . Один из знамена-

телей этих дробей отличен от нуля, а соответствующий числитель может принимать любые значения, поэтому параметр t может принимать любые вещественные значения. Учитывая, что каждое из отношений равно t, по-

лучим параметрические уравнения прямой:

x = x0 +lt , y = y0 + mt , z = z0 + nt .	(3.21)
Пусть плоскость π задана общим уравнением	Ax + By +Cz + D = 0 , а
прямая L − параметрическими уравнениями x = x0 +lt ,	y = y0 + mt , z = z0 + nt .

Точка M (x , y , z ) пересечения прямой L и плоскости π должна одновременно принадлежать плоскости и прямой. Это возможно только в том слу-

чае, когда параметр				t	удовлетворяет уравнению Ax0 + By0 +Cz0 + D +
+t(Al + Bm +Cn) = 0 ,			т. е.	t = − Ax0 + By0 +Cz0 + D . Таким образом, точка пере-
						Al + Bm +Cn
сечения прямой и плоскости имеет координаты
	=	Bmx0 +Cnx0 −l(By0			+Cz0	+ D)	,
x		Al	+ Bm +Cn
	=	Aly0 +Cny0	− m(Ax0		+Cz0	+ D)	,
y		Al	+ Bm +Cn
z	=	Alz0 + Bmz0 − n(Ax0 + By0 + D) .
		Al + Bm +Cn
							69

	П р и м е р 32.				Составить параметрические уравнения прямой, про-
ходящей через точки A(3, −1, 2) и B (2,1,1) .
	Решение. За направляющий вектор прямой возьмем вектор									AB =
= {−1, 2, −1}. Прямая проходит через точку A,									поэтому по формуле (3.21)
искомые уравнения прямой имеют вид x = 3 −t ,									y = −1+ 2t , z = 2 −t .
	П р и м е р 33.				Вершины треугольника ABC имеют координаты
(3, 6, −7) , (−5, 2, 3)			и (4, −7, − 2) соответственно. Составить параметрические
уравнения медианы, проведенной из вершины C .
	Решение.		Пусть			M(x0 , y0 , z0 )		− середина стороны AB ,		тогда
x0 =	3 −5	= −1, y0	=	6 + 2	= 4	, z0 =	−7 +3	= −2 . В качестве направляющего век-
2			2			2

тора медианы возьмем вектор СM = {−5,11, 0}. Тогда параметрические уравнения медианы имеют вид x = 4 −5t , y = −7 +11t , z = −2 .

П р и м е р 34. Составить канонические уравнения прямой, проходя-

щей через точку M0 (2, 3, −5)

3x − y + 2z −7 = 0

.

параллельно прямой

x +3y − 2z +3 = 0

Решение. Прямая задана как линия пересечения плоскостей с нор-

мальными векторами N1 = {3, −1, 2} и N2 = {1, 3, − 2}. В качестве направляюще-

го

вектора

a

этой

прямой

возьмем вектор

N1 × N2 , т.

е.

a =

i

j

k

= {− 4, 8,10}. Согласно

(3.18) искомое уравнение имеет

вид

3

−1

2

1

3

− 2

x − 2

=

y −3

=

z +5

или

x − 2

=

y −3

=

z +5

.

− 4

8

10

2

− 4

−5

3.8.Угол между прямыми в пространстве. Угол между прямой

иплоскостью

Пусть две прямые L1

и L2

в пространстве заданы своими канониче-

скими уравнениями

x − x1

=

y − y1

=

z − z1

и

x − x2

=

y − y2

=

z − z2

. Тогда один

l

m

n

l

m

n

1

1

1

2

2

2

из углов ϕ между этими прямыми равен углу между их направляющими

векторами a1 = {l1,m1,n1} и a2	= {l2 ,m2 ,n2}. Воспользовавшись формулой (2.22),
для определения угла ϕ получим формулу
cosϕ =				l1l2 + m1m2 + n1n2												.	(3.22)
		l	2	2	+ n	2				l	2	2	+ n	2
				+ m								+ m
	1			1	1				2			2	2
Второй угол ψ между этими прямыми равен π −ϕ и cosψ = −cosϕ .
Условие параллельности прямых L1												и L2	равносильно условию кол-
линеарности векторов a1 = {l1,m1,n1} и a2									= {l2 ,m2 ,n2} и заключается в пропор-
					70

циональности их координат, т. е. условие параллельности прямых имеет вид

l1	=	m1	=	n1	.	(3.23)
l		m
				n
2		2		2

Если прямые L1 и L2 перпендикулярны, то их направляющие векто-

ры ортогональны, т.е. условие перпендикулярности определяется равенством

					l1l2 + m1m2 + n1n2 = 0.
	Рассмотрим				плоскость	π , заданную общим
Ax + By +Cz + D = 0 , и прямую						L, заданную каноническими
x − x0	=	y − y0	=	z − z0	= t .
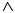l		m		n

N

a

ψ

ϕ

(3.24)

уравнением

уравнениями

L

π

Угол ϕ между прямой L и плоскостью π является дополнительным к углу ψ между направляющим вектором прямой и нормальным вектором

плоскости, т. е. ϕ =

π

π

N a

−ψ

и sinϕ = sin

−ψ

= cosψ =

, или

2

a

2

N

sinϕ =

Al + Bm +Cn

.

(3.24)

2

+ B

2

+C

2

l

2

2

+ n

2

A

+ m

Условие параллельности прямой L и плоскости π эквивалентно условию перпендикулярности направляющего вектора прямой и нормального вектора плоскости, т. е. скалярное произведение этих векторов должно равняться нулю:

Al + Bm +Cn = 0.

(3.25)

Если же прямая перпендикулярна плоскости, то направляющий вектор прямой и нормальный вектор плоскости должны быть коллинеарны. В этом случае координаты векторов пропорциональны, т. е.

	A		=	B		=	C .	(3.26)
	l			m
							n
П р и м е р 35. Найти тупой угол между прямыми x = 3t − 2 ,								y = 0 ,

z = −t +3 и x = 2t −1, y = 0 , z = t −3.

Решение. Направляющие векторы этих прямых имеют координаты {3, 0, −1} и {2, 0,1}. Поэтому один угол ϕ между прямыми определяется со-

71

отношением cosϕ =

2 3 + 0 + (−1) 1

=

5

=

1

, т. е.

ϕ =

π π .

32 + 02 + (−1)2 22 + 02 +12

5 2

2

4 2

Поэтому условию задачи удовлетворяет второй угол между прямыми, равный π − π4 = 34π .

3.9. Расстояние от точки до прямой в пространстве

Пусть M − точка пространства с координатами (x1, y1, z1) , L − прямая,

заданная каноническими уравнениями

x − x0

=

y − y0

=

z − z0

.

Найдем рас-

стояние d от точки M

до прямой L.

l

m

n

M

d

L

M0 (x0 , y0 , z0 )

a

Приложим направляющий вектор a = {l,m,n} к точке M0 (x0 , y0 , z0 ) . Рас-

стояние d от точки M (a,b,c)

до прямой

L является высотой параллело-

грамма, построенного на векторах a

и M0M . Найдем площадь параллело-

грамма, используя векторное произведение:

S

=

=

y

− y z − z

2

z

− z x − x

2

+

x

− x y

− y

2

M0M ×a

1

0

1

0

+

1

0

1

0

1

0

1

0

.

m

n

a

n

l

l

m

С

другой

стороны,

.

Из

равенства правых

S = d

= d

l2 + m2 + n2

частей двух последних соотношений следует, что

y − y z − z

2

+

z − z x − x

2

x − x y − y

2

1

0

1

0

1

n

0

1

0

+

1

0

1

0

d =

m

n

nl

l

m

.

(3.27)

l2 + m2 + n2

3.10. Эллипсоид

Определение. Эллипсоидом называется поверхность второго порядка, которая в некоторой системе координат определяется уравнением

	x2	+	y2	+	z2	=1.	(3.28)
	a2		b2		c2

Уравнение (3.28) называется каноническим уравнением эллипсоида. Из уравнения (3.28) следует, что координатные плоскости являются

плоскостями симметрии эллипсоида, а начало координат − центром симметрии. Числа a, b, c называются полуосями эллипсоида и представляют

72

собой длины отрезков от начала координат до пересечения эллипсоида с осями координат. Эллипсоид представляет собой ограниченную поверхность, заключенную в параллелепипеде x ≤ a , y ≤ b , z ≤ c .

Установим геометрический вид эллипсоида. Для этого выясним форму линий пересечения его плоскостями, параллельными координатным осям.

Для определенности рассмотрим линии пересечения эллипсоида с плоскостями z = h , параллельными плоскости Oxy . Уравнение проекции

линии пересечения на плоскость Oxy получается из (3.28), если в нем положить z = h . Уравнение этой проекции имеет вид

	x2	+	y2	=1− h2 .	(3.29)
	a2		b2
				c2

Если h c , то (3.29) является уравнением мнимого эллипса и точек пересечения эллипсоида с плоскостью z = h нет. Отсюда и следует, что

z

≤ c .

Если

h

= c , то линия (3.29) вырождается в точки, т. е.

плоскости

z = ±c

касаются эллипсоида в точках

(0, 0, −c) и (0, 0, c) . Если

h

c , то

1− h2

0 и можно ввести обозначения

c2

a = a 1−

h2

, b

= b 1

−

h2

.

(3.30)

c2

c2

Тогда уравнение (3.29) принимает вид

x2

+

y2

=1,

(3.31)

(a )2

(b )2

т. е. проекция на плоскость Oxy линии пересечения эллипсоида и плоско-

сти z = h представляет собой эллипс с полуосями, которые определяются равенствами (3.30). Так как линия пересечения поверхности плоскостями, параллельными координатным, представляет собой проекцию, «поднятую» на высоту h , то и сама линия пересечения является эллипсом.

При уменьшении значения h полуоси a и b увеличиваются и достигают своего наибольшего значения при h = 0 , т. е. в сечении эллипсоида координатной плоскостью Oxy получается самый большой эллипс с полу-

осями a = a и b = b .

z

y O

x

73