Analiticheskaya_Geometria

O(0,0) совпадало с серединой отрезка F1F2 . Обозначим F1F2 = 2c , r1 − r2 = 2a ,

2a 2c , где r1 , r2 − фокальные радиусы (расстояния от дочки до фокусов) точки гиперболы. Тогда фокусы F1 и F2 имеют координаты F1(−c,0) , F2 (c,0) .

y	M(x, y)

r1

r2

x

F1(−c,0)

O

F2 (c,0)

Пусть M(x, y) − произвольная точка гиперболы. Имеем:

r1 =

F1M

,

r2 =

F2M

. Из определения гиперболы

r1 − r2

= 2a ,

(1.32)

или (x + c)2 + y2 − (x −c)2 + y2 = ±2a − искомое уравнение гиперболы. Приведем это уравнение к более удобному виду. Из последнего равенства следует, что (x + c)2 + y2 = ±2a + (x −c)2 + y2 .Так как (x −с)2 + y2 4a2 , то можем обе части уравнения возвести в квадрат, и после эквивалентных преобразований получим: ± a (x −c)2 + y2 = cx − a2 . Следовательно,

(c2 − a2 )x2 − a2 y2 = a2 (c2 − a2 ) . Введем новую переменную b =					c2 − a2	. Тогда
b2 x2 − a2 y2 = a2b2 , или
	x2	−	y2	=1.	(1.33)
	a2		b2

Таким образом, из уравнения (1.32) следует уравнение (1.33), т. е. координаты всех точек гиперболы удовлетворяют соотношению (1.33). Покажем, что верно и обратное, т. е. множество точек плоскости, координаты которых удовлетворяют уравнению (1.33), является гиперболой.

Пусть координаты некоторой точки M(x, y) плоскости удовлетворя-

ют уравнению (1.33),

тогда y

= b

2

= (c

− a

2

. Для фокальных

2

−1

)

2 −1

2

2

x

2

2

x

a

a

радиусов этой точки

имеем:

2

= (x + c)

2

+ y

2

cx 2

2

(x −c)

2

+ y

2

=

r1

= a +

,

r2 =

a

cx 2

до фокусов

= a −

, поэтому модуль разности расстояний точки M(x, y)

a

24

2

2

2

2

2

=

2

2

=

2

+

c

x

+

a

2

−

c

x

= 2a . Следователь-

r1 − r2

= (r1 − r2 )

r1

+ r2

− 2r1r2

2 a

a

2

a

2

но, точка M(x, y)

является точкой гиперболы.

Уравнение (1.33) называется каноническим уравнением гиперболы. Гипербола симметрична относительно осей координат и относительно начала координат. Оси симметрии гиперболы называются ее осями, а

центр симметрии − центром гиперболы.

Рассмотрим часть гиперболы, расположенной в I четверти коорди-

натной плоскости. Пусть точка

M(x0 , y)

принадлежит гиперболе. На пря-

b

b

b

b

2

2

2

мой

y = a x возьмем точку

N(x0

,Y) . Тогда

Y = a x0

= a

x0

a

x0

− a

= y и

= Y − y =

b

b

b

b

при

MN

2

2

2

2

a x0

− a

x0 − a

= a (x0 −

x0

− a

) =

→ 0

x0 +

x02 − a2

x0 → +∞ . Поэтому прямые y = ± b x являются асимптотами гиперболы.

a

y

В1

b

а

В2

F1

A1

O

A2

F2

x

С1

С2

Точки A1(−a,0)		и A2 (a,0)			пересечения гиперболы с осью Ox называют-
ся ее вершинами,		ось Ox			− ее действительной	осью, прямоугольник
С1С2B2B1 − основным прямоугольником гиперболы, a						и b − соответственно
действительной и мнимой полуосями.
У гиперболы различают правую и левую ветви, расположенные в по-
луплоскостях x 0 и x 0 соответственно.
Уравнение	x2	−	y2	= −1 также определяет гиперболу, которая изобра-
	a2
			b2

жена на рисунке пунктирной линией. Эта гипербола называется сопряжен-

	ной к гиперболе	x2	−	y2	=1 и имеет такие же асимптоты.
		a2		b2
	Гипербола с равными полуосями (a = b ) называется равносторонней,

и ее каноническое уравнение имеет вид x2 − y2 = a2 ( y2 − x2 = a2 ). Ее основ-

ным прямоугольником является квадрат, а асимптоты взаимно перпендикулярны.

25

Определение. Эксцентриситетом гиперболы ε называется отно-

шение aс , где c − половина расстояния между фокусами, a − действительная полуось, т. е.

ε =

c

.

(1.34)

a

b 2

Так как

2

c2

a2

+b2

b

2

ε

=

=

= 1+

, то

=

ε

−1

. Если b → a , то

a2

a2

a

a

ε → 2 . Если b → 0, то ε →1. Эксцентриситет гиперболы характеризует форму ее основного прямоугольника, т. е. и саму гиперболу.

П р и м е р 17. Составить уравнение гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала коорди-

нат, если расстояние между фокусами 2c =10 и эксцентриситет ε = 53 .

Решение. Так как расстояние между фокусами 2c =10 , то c = 5 и фокусы, расположенные на оси ординат, имеют координаты (0, −5) и (0, 5) .

Вещественной полуосью гиперболы является b . Учитывая, что эксцентриситет гиперболы равен отношению c к вещественной полуоси, находим

		c	= 3. Тогда a =				= 4. Искомое уравнение гиперболы
	b =			c2 −b2	=
						25 −9
		ε

имеет вид x2 − y2 = −1.

16 9

1.14. Директрисы эллипса и гиперболы

Определение. Две прямые, перпендикулярные большой оси эллипса

	и расположенные симметрично относительно центра на расстоянии	a	от
		ε

него, называются директрисами эллипса, т. е. директрисы эллипса зада-

ются уравнениями x = ±

a

(ε 1).

ε

у

M (x; y)

d

r1

r

с

2

А

х

F2

a

a

−

F1

О

a

ε

ε

Теорема 5. Если r − расстояние произвольной точки M(x, y) эллипса до какого-либо фокуса, а d − расстояние той же точки до соответствую-

26

щей этому фокусу директрисы, то отношение										r	есть величина постоянная,
равная эксцентриситету эллипса.										d
						a
Доказательство. Пусть D1								, y	− точка правой директрисы эллипса,
					a	ε
тогда d =		MD1		=		− x. Расстояние		r	точки M(x, y) до соответствующего
					ε

фокуса F2 (c,0) : r = 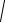(x −c)2 + y2 = = a − cxa = a −εx. Таким образом, dr

2

2

2

2

x

2

c

2

x

− 2xc + c

+ (a

−c

2

=

a −

x

=

) 1−

a

a

=aa−εx = ε , теорема доказана.

ε− x

Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на рас-

стоянии εa от него, называются директрисами гиперболы, т. е. директри-

сы гиперболы задаются уравнениями x = ±

a

(ε 1), где a

− вещественная

ε

полуось,

ε − эксцентриситет гиперболы.

Теорема 6. Если r

− расстояние произвольной точки M(x, y) гипер-

болы

x2

−

y2

=1 до какого-либо фокуса,

а d

− расстояние той же точки до

b2

a2

r

соответствующей этому фокусу директрисы, то отношение

есть величи-

d

на постоянная, равная эксцентриситету гиперболы.

Доказательство. Пусть

a

D1

, y − точка правой директрисы гипер-

ε

болы, тогда d =

MD1

=

a

− x

= x

−

a

, так как x

≥ a

,

a

a . Расстояние r точки

ε

ε

ε

до

соответствующего

фокуса

F2 (c,0) :

M(x, y)

r =

(x −c)2 + y2 =

2

2

2

2

x

2

c

2

c

c

x − a = εx − a . Получи-

− 2xc + c

+ (a

x

= x

−c

2

a −

x

=

a

−

=

) 1−

a

=

a

a

a

ли, что

r

εx − a

=

= ε . Теорема доказана.

d

a

x − ε

На основании доказанных теорем можно дать следующее определение эллипса и гиперболы.

Определение. Множество точек плоскости, для которых отношение расстояний до фокуса и до соответствующей фокусу директрисы является постоянной величиной, равной ε , есть эллипс, если ε 1, и гипербола, если ε 1.

П р и м е р 18. Составить уравнение эллипса, фокусы которого расположены на оси абсцисс симметрично относительно начала координат,

27

если дана точка M1 (−5, 2) эллипса и расстояние между его директрисами

равно 10.

Решение. Для того чтобы составить уравнение заданного эллипса, надо найти его полуоси. Координаты точки M1 (−5, 2) удовлетворяют

уравнению эллипса, поэтому a52 + b42 =1. Фокусы эллипса расположены на оси абсцисс, вследствие чего расстояние d между директрисами определя-

ется по формуле

2a

2a2

.

Поэтому

2a2 =10c =10

,

или

d =

=

a2 −b2

ε

4a2

c

a4 = 25a2 − 25b2 . Так как b2

=

, то уравнение относительно a2 принима-

a2 −5

ет вид a4 −30a2 − 225 = 0 , т. е. a2

=15

и соответственно b2

= 6 . Таким обра-

зом, искомое уравнение эллипса

x2

+

y2

=1.

15

6

П р и м е р 19.

Эксцентриситет гиперболы ε = 3,

расстояние

d

от

точки M гиперболы до директрисы равно 4. Вычислить расстояние r

от

точки M до фокуса, одностороннего с этой директрисой.

Решение. По определению гиперболы

r

= ε , поэтому r = dε =12 .

d

1.15. Парабола

Определение. Параболой называется множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус, т. е. ε =1.

Выберем прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус перпендикулярно директрисе. Положительное направление оси − от директрисы к фокусу. Начало системы координат находится на одинаковом расстоянии от фокуса и директрисы.

					y
		p		d	M(x, y)
Q	−		, y
		2
					r
								x
				O	p
					F		,0
						2

Пусть M(x, y) − произвольная точка плоскости; d − расстояние точки M до директрисы; p − расстояние от фокуса до директрисы. Тогда дирек-

28

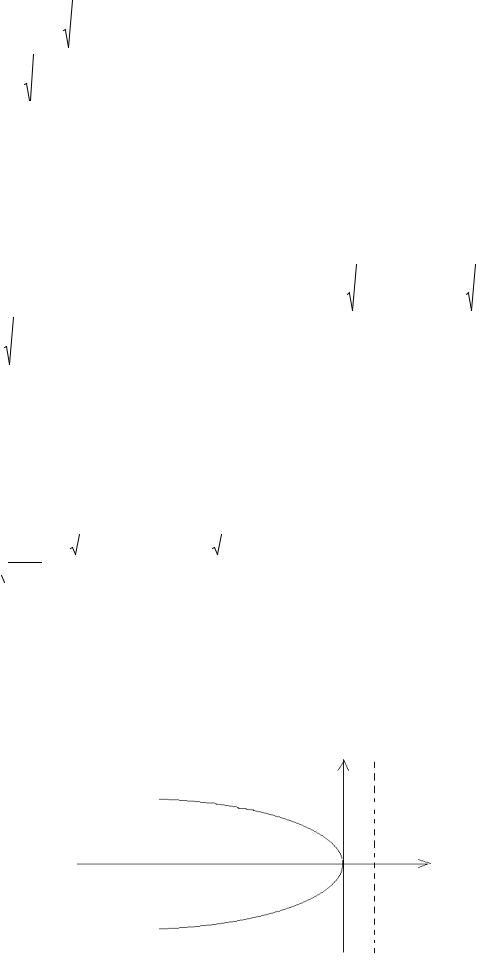
	триса задается уравнением	x = −	p	, фокус F	имеет координаты	p		,0		и
			2				2

p

2

2

,

p

.

Согласно определению параболы

r =

MF

=

x

−

+ y

d = x +

d = r

2

2

или

p

2

2

p

. Из последнего равенства получаем

x −

+ y

= x +

2

2

y2

= 2 px.

(1.35)

Уравнение (1.35)

называется каноническим уравнением параболы.

Покажем,

что любая точка M(x, y) , координаты которой удовлетво-

ряют уравнению (1.35), является точкой гиперболы.

Координаты точки M(x, y) удовлетворяют уравнению (1.35), поэтому

x ≥ 0 и расстояние d

этой точки до прямой x = −

p

:

d =

p

+ x . Расстояние r

2

2

точки

p

p

2

2

p 2

M(x, y)

до

фокуса

F

,0 :

r =

x −

+ y

=

x −

+ 2 px =

2

2

2

p 2

p

= d , т. е. точка M(x, y)

является точкой гиперболы.

=

x +

= x +

2

2

Уравнение (1.35) − это уравнение второй степени, поэтому парабола − кривая второго порядка.

Парабола симметрична относительно оси Ox и проходит через точку O (0, 0) . Точка O (0, 0) называется вершиной параболы, ось симметрии (ось

Ox ) − ее осью симметрии, а расстояние p от фокуса до директрисы − па-

раметром.			x = x0 0 .	На параболе имеются две точки с абсциссой
Рассмотрим
x0 : M1(x0 ,		)	и M2 (x0 ,−		) . Эти точки находятся на расстоянии
	2 px0			2 px0

22 px0 друг от друга, т. е. чем больше параметр p , тем шире область, ле-

жащая внутри параболы.

Если система координат выбрана таким образом, что ось абсцисс совмещена с осью параболы, а начало координат − с вершиной, но ось Ox направлена от фокуса к директрисе, то уравнение параболы записывается в

виде
y2 = −2 px .	(1.36)
	y

	F O	p	x
		2

Если начало координат совмещено с вершиной параболы, а ее ось − с осью ординат, то уравнение параболы имеет вид

x2 = 2 py

(1.37)

и парабола лежит в верхней полуплоскости. Если же парабола расположена в нижней полуплоскости, то она задается уравнением

x 2 = −2 py .

(1.38)

Каждое из уравнений (1.36) − (1.38), как и уравнение (1.35), называется каноническим уравнением параболы.

П р и м е р 20. Составить уравнение параболы, вершина которой находится в начале координат, зная, что парабола расположена симметрично относительно оси Oy и проходит через точку C (1,1) .

Решение. Осью параболы является ось ординат, поэтому уравнение имеет вид, определяемый уравнением (1.37) или (1.38). Точка С располо-

жена в верхней полуплоскости, поэтому x2 = 2 py , и значение параметра p находится из уравнения 12 = 2 p 1. Таким образом, p = 12 , и искомое уравне-

ние имеет вид x2 = y .

П р и м е р 21. Составить уравнение параболы, если даны ее фокус F (7, 2) и директриса x −5 = 0 .

Решение. По формуле (1.15) расстояние d от фокуса до директрисы d = 7 −5 = 2 , поэтому параметр параболы p = 2 . Прямая, проходящая через

фокус перпендикулярно директрисе, задается уравнением y = 2 и является

осью симметрии параболы. Вершина параболы расположена на ее оси на одинаковом расстоянии от фокуса и директрисы, т. е. имеет координаты (6, 2) . Положительное направление от директрисы к фокусу совпадает с

положительным направлением оси Ox . Таким образом, искомое уравнение

имеет вид (y − 2)2 = 4(x −6) или x = 1 y2 − y + 7 .
4
1.16. Общее уравнение линии второго порядка
Общее уравнение линии второго порядка имеет вид
Ax2 + 2Bxy +Cy2 + 2Dx + 2Ey + F = 0 ,	(1.39)

где A, B,C, D, E, F −const , A2 + B2 +C2 ≠ 0 .

Лемма. Пусть в прямоугольной системе координат Oxy задано урав-

нение (1.39) и AC − B2 ≠ 0. Тогда с помощью параллельного сдвига и последующего поворота осей на некоторый угол уравнение (1.39) приводится к

виду:	+C (y )		+ F		= 0 ,	(1.40)
A(x )
′ ′′ 2	′ ′′	2		′
		30

′

′

′

−const ,

′′

′′

координаты точек в новой системе координат.

где A,C , F

x , y −

Доказательство. Параллельным переносом сдвинем начало коорди-

нат O(0,0) в точку

′

′

′

. В новой системе ко-

O (x0 , y0 ) . Тогда x = x + x0 ,

y = y + y0

ординат

′

′ ′

O x y уравнение (1.39) примет вид

, или

′

2

′

′

′

2

′

′

A(x

+ x0 )

+ 2B(x

+ x0 )(y + y0 ) +C(y + y0 )

+ 2D(x + x0 ) +

2E(y + y0 ) + F = 0

′

2

′ ′

′

2

′ ′

′ ′

+ F

′

=

0 ,

(1.41)

A(x )

+ 2Bx y +C(y )

+ 2D x + 2E y

где D′ = Ax0 + By0 + D ,

E′ = Bx0 +Cy0 + E ,

F ′ = Ax02 + 2Bx0 y0 +Cy02 + 2Dx0 + 2Ey0 + F .

В уравнении (1.41) коэффициенты D′

и E′

обращаются в нуль, если по-

добрать x0 , y0 так, чтобы

Ax

+ By

+ D

= 0,

(1.42)

0

0

= 0.

Bx0 +Cy0 + E

По теореме Крамера система (1.42) имеет единственное решение, так

как AC − B2

≠ 0: x0

= − DC + BE ,

y0 =

− AE + BD

. Уравнения (1.42) называются

AC − B2

AC − B2

уравнениями центра линий второго порядка, а точка (x0 , y0 ) − центром этой

линии. При параллельном сдвиге начала прямоугольной системы координат в точку (x0 , y0 ) уравнение (1.41) принимает вид

A(x )

+ 2Bx y +C(y )

+ F

= 0 .

(1.43)

Пусть O x y

′ 2

′

′

′

2

′

− прямоугольная система координат, полученная пово-

′ ′′ ′′

′

′ ′

. Координаты точек плоскости в этом слу-

ротом на угол α системы O x y

чае преобразуются по формулам (1.17):

′

′′

′′

′

′′

′′

x = x

cosα − y sinα

, y = x

sinα + y cosα .

Уравнение (1.43) в прямоугольной системе координат

′

′′ ′′

O x y прини-

мает

вид

′′

′′

2

+

′′

′′

′′

′′

′′

A(x cosα − y sinα)

2B(x cosα − y sinα)(x sinα + y cosα) +C(x sinα +

′′

2

+ F

′

= 0 , или

+ y cosα)

0 ,

(1.44)

′ ′′

2

′

′′ ′′

′

′′

2

+ F

′

=

где

A(x )

+ 2B x y +C (y )

′

2

α +

2Bcosαsinα

+C sin

2

α ,

′

2

α −sin

2

α) +

A =

Acos

B

= −Acosαsinα + B(cos

+C sinαcosα ,

С′ = Asin2 α − 2Bcosαsinα +C cos2 α .

Выберем угол α

таким образом,

чтобы коэффициент

′

был равен

B

нулю, т. е. 2Bcos2α −(A−C)sin 2α = 0 , или

2Bcos2α = (A−C)sin 2α .

(1.45)

Если

A = C ,

то cos2α = 0 , и можно взять α

= π . Если

A ≠ C ,

то из

2B

4

= 1 arctg

2B

уравнения (1.45) tg2α =

, и поэтому существует угол α

,

A−C

2

A−C

при котором выполняется условие (1.45). При повороте осей координат на соответствующий угол α уравнение (1.44) приводится к виду (1.40). Лемма доказана.

Коэффициенты A, B,C не меняются при параллельном переносе сис-

темы координат, но изменяются при повороте осей. Легко проверить, что выражение AC − B2 является инвариантом общего уравнения линий второго

31

порядка, т. е. не меняется при повороте осей. В зависимости от выражения AC − B2 ( A′C′−(B′)2 ) выделяют три типа линий второго порядка:

1)эллиптический (AC − B2 0 );

2)гиперболический (AC − B2 0 );

3)параболический (AC − B2 = 0 ).

Рассмотрим линии второго порядка эллиптического типа. Так как для эллиптического типа AC − B2 ≠ 0, то в некоторой системе координат

общее уравнение может быть приведено к виду
Ax2 +Cy2 + F = 0 .	(1.46)

Возможны три случая:

a)если AC 0, ACF 0 , то − FA 0 , − CF 0 , поэтому можно вве-

сти обозначения

a2 = −

F

,

b2

= −

F

, с и спользованием которых уравнение

A

C

(1.46) приводится к уравнению (1.30) эллипса:

x2

+

y2

=1;

a2

b2

AC 0,

AF 0 ,

то из (1.46)

получаем уравнение

b)

если

Ax2 +Cy2

= −F , разделив

обе

части

которого на F

и обозначив a2 =

F

,

A

b2 = CF , получим уравнение мнимого эллипса:

		x2	+	y2	= −1;		(1.47)
		a2
				b2
c) если AC 0, F = 0 , то, сделав замену						A = a2 , C = b2 ( A 0,	B 0)
или A = −a2 , C = −b2 ( A 0 ,	B 0 ), приведем уравнение (1.46) к уравнению
пары мнимых пересекающихся прямых:
	a2 x2 +b2 y2 = 0 .						(1.48)

Уравнение линии второго порядка гиперболического типа в некоторой системе координат также может быть приведено к виду (1.46), так как

AC − B2 ≠ 0:

a) если A 0 ,

C 0 , F ≠ 0 или

A 0 ,

C 0 ,

F ≠ 0 , то соответствую-

щей заменой (например, для случая

A 0,

C 0 ,

F 0 можно сделать за-

мену a2

= −

F

, b2

=

F

) уравнение (1.46) приводится к уравнению (1.33) ги-

A

C

перболы:

x2

−

y2

=1;

a2

b2

b) если A 0,

C 0 , F = 0 или A 0 , C 0 , F = 0 , то, положив a2 = A,

b2 = −C ( a2 = −A,

b2

= C ), получим уравнение пары пересекающихся веще-

ственных прямых

a2 x2 −b2 y2

= 0 .

(1.49)

32

Уравнения линий второго порядка параболического типа не могут быть приведены к уравнению вида (1.46), но с помощью поворота осей на угол α , указанный в лемме, их можно привести к виду

Ax2 +Cy2 + 2Dx + 2Ey + F = 0 .	(1.50)
Коэффициенты уравнения линии второго порядка параболического
типа удовлетворяют условию AC − B2 = 0 . В уравнении (1.50)	B = 0 , следо-

вательно, AC = 0 . Пусть A = 0 , тогда C ≠ 0 (если C = 0 , то уравнение линии становится уравнением первого порядка). Уравнение (1.50) принимает вид

Cy2 + 2Dx + 2Ey + F = 0 , или

E 2

E2

= 0 .

(1.51)

C y +

+ 2Dx + F −

C

C

Параллельным

переносом

переместим

начало

координат в

точку

E

′ ′ ′

0, −

. Уравнение (1.51) в новой системе координат

C

O x y примет вид

C(y )

+ 2Dx + F

= 0 ,

(1.52)

′

2

′

′

′

E

′

′

E2

где

+ C

,

F

= F −

C .

y

= y

x = x ,

+

1. Если

D ≠ 0 , то уравнение (1.52) приводится к уравнению С(y )

′ 2

+ 2D

′

F ′

′′

′′ ′′

,

полученной

x

+

= 0 . В прямоугольной системе координат O x y

2D

′

′

′

F ′

из

параллельным переносом начала координат в точку −

, 0

,

O x y

2D

x = x + 2D ,

y

= y

и уравнение (1.52) принимает вид C(y )

+ 2Dx = 0 . Если

′′

′

F ′

′′

′

′′ 2

′′

= − D ( p =

D

CD 0

(CD 0) , то, обозначив

p

), получим уравнение (1.35)

параболы:

C

C

′′

2

=

′′

(y )

2 px .

то уравнение (1.52)

имеет вид C(y )

+ F

= 0 . Введем

2. Если

D = 0 ,

′ 2

′

обозначение

a

2

=

F ′

. Тогда при CF

′

0

получим уравнение пары вещест-

C

венных параллельных прямых

−a

= 0 .

(1.53)

(y )

′ 2

2

Если CF ′ 0 , то будет пара мнимых параллельных прямых, задаваемых уравнением (y′)2 + a2 = 0 .

При F ′ = 0 получим пару совпадающих прямых, задаваемых уравнением (y′)2 = 0 .

Замечание. В случае, когда A ≠ 0 , C = 0 уравнение (1.50) линии второго порядка параболического типа также приводится к каноническим уравнениям параболы, пары мнимых параллельных прямых, пары параллельных прямых или пары совпадающих прямых.

Используя вспомогательную лемму и различные типы линий второго порядка, доказали теорему.

33