Analiticheskaya_Geometria

x В

Обозначим OMx = прOxOM , OMy = прOy OM , OMz = прOz OM . Тогда OMx +

+OMy +OMz = OB +OMz = OM = a , т. е. a = OMx +OMy +OMz . Векторы OMx и

i коллинеарны,	поэтому существует такое число λ , что OMx = λi . Анало-
гично можно	показать,	что	OMy = µj				и OMz =νk .	Таким образом,
a = λi + µj +νk .									λ = X , µ = Y ,
Для доказательства		единственности					установим,	что
ν = Z , где X,Y,Z − координаты вектора a . Если вектор OMx									имеет такое же
направление, как и вектор i ,			то X =		OMx		и OMx = Xi .	Если же векторы

OMx и i противоположно направлены, то OMx = OMx (−i ) = −X (−i ) = Xi . С

другой стороны, OMx = λi . Из равенства векторов следует, что λ = X . Равенства µ = Y и ν = Z доказываются аналогично. Теорема доказана.

Определение. Три вектора, лежащие в одной плоскости или в параллельных плоскостях, называются компланарными.

Определение. Векторы a1,a2 ,...,an называются линейно зависимыми, если найдутся такие вещественные числа α1,α2 ,...,αn , из которых хотя бы одно отлично от нуля, что существует тривиальная линейная комбинация

этих векторов, т. е.
α!a1 +α2a2 +... +αnan = 0 .	(2.12)
Теорема 6. Необходимым и достаточным условием линейной зави-
симости трех векторов является их компланарность.
Доказательство. Необходимость. Пусть три вектора a , b	и c ли-

нейно зависимы. Докажем компланарность этих векторов. По определению линейной зависимости найдутся такие вещественные числа α , β и γ , из

которых хотя бы одно отлично от нуля, что αa + βb +γc = 0 . Для определенности будем считать, что α ≠ 0 . Тогда a = −αβ b −αγ c , или a = λb + µc . Если

векторы a , b и c приложены к общему началу O , то вектор a равен диагонали параллелограмма, построенного на векторах λb и µc как на смеж-

ных сторонах, следовательно, векторы a , λb и µc лежат в одной плоско-

сти. Это равносильно тому, что и векторы a , b и c лежат в одной плоскости, так как после приведения к общему началу векторы b и λb (соответственно, c и µc ) лежат на одной прямой.

Достаточность. Пусть векторы a , b и c − компланарны. Если ка- кие-либо два вектора из них являются коллинеарными, то они будут л и- нейно зависимыми, следовательно, и все три вектора линейно зависимы.

44

А′			С
А		с
a	b	В		′
О				B
Пусть в тройке векторов a , b , c			ни одна пара векторов не является

коллинеарной. Тогда в этой тройке отсутствуют и нулевые векторы. Перенесем три компланарных вектора a , b , c на одну плоскость и приведем их к общему началу O . Обозначим буквами A, B и C концы этих векторов.

Через точку C проведем прямые, параллельные векторам a и b .

Точки пересечения построенных прямых с прямыми, на которых лежат векторы a и b , обозначим соответственно A′ и B′. Эти точки существуют, так как векторы a и b не коллинеарны. Из параллелограмма OA′CB′

следует, что c = OA′+OB′. Вектор OA′ коллинеарен вектору a , поэтому существует вещественное число λ такое, что OA′ = λa . Аналогично доказывается, что OB′ = µb . Таким образом, вектор c является линейной комбинацией векторов a и b и, следовательно, λa + µb −c = 0 . Это равносильно тому, что векторы a , b и c линейно зависимы. Теорема доказана.

Рассмотрим три компланарных вектора a = {X ,Y,Z }, b = {X ,Y ,Z },

1 1 1 2 2 2

c = {X3,Y3,Z3}. Составим матрицу A, столбцами которой являются коорди-

наты этих векторов. Столбцы матрицы линейно зависимы тогда и только тогда, когда определитель этой матрицы равен нулю. Таким образом, не-

обходимым и достаточным условием компланарности векторов a , b и c является равенство нулю определителя матрицы, столбцами которой являются координаты этих векторов, т. е.

					X1 X2 X3			= 0 .	(2.13)
					Y1	Y2 Y3
					Z1 Z2 Z3
Теорема 7. Если			p ,	q , r		− произвольные некомпланарные векторы,
то любой вектор a		может быть представлен единственным образом в виде
				a =αp + βq + γr ,					(2.14)
где α, β, γ − некоторые числа,						т. е. любой вектор может быть разложен по
трем некомпланарным векторам.
Доказательство. Пусть векторы a , p , q ,									r заданы своими коорди-
натами, т. е.	a = {X,Y,Z},			p = {X1,Y1,Z1}, q = {X2 ,Y2 ,Z2}, r = {X3,Y3,Z3}. Тогда
a = Xi +Yj + Zk .	По правилу сложения векторов и умножения вектора на
число имеем:		αp + βq +γr =				(αX1 + βX2 +γX3 )i +			(αY1 + βY2 +γY3 ) j + (αZ1 + βZ2 +

+γZ3 )k . Для выполнения условия (2.14) система уравнений

45

αX					+ βX		2	+γX = X
			1					3			(2.15)
αY1 + βY2 +γY3 = Y
αZ1 + βZ2 +γZ3 = Z
относительно неизвестных α ,				β и γ				должна иметь единственное решение.
Определитель системы ∆ =		X1			X2	X3				≠ 0 , так как векторы p , q , r	неком-
		Y1			Y2		Y3
		Z1			Z2		Z3

планарные. Следовательно, по теореме Крамера система (2.15) имеет единственное решение, и вектор a может быть единственным образом представлен в виде a =αp + βq + γr . Теорема доказана.

П р и м е р 23.	Даны векторы p = {3, − 2,1}, q = {−1,1, − 2},	r = {2,1, −3}.
Найти разложение вектора c = {11, −6, 5} по базису p , q , r .
Решение. Для разложение вектора с по базису p , q , r		необходимо
найти такие числа α ,	β и γ , чтобы выполнялось равенство с = αp + βq +γr .

Если два вектора равны, то равны и их соответствующие координаты, по-

		3α − β + 2γ =11,
этому относительно α ,	β и γ имеем систему уравнений
		− 2α + β +γ = −6,
		α − 2β −3γ = 5.

Векторы p , q , r по условию задачи образуют базис, поэтому главный оп-

ределитель системы отличен от нуля и по теореме Крамера она имеет единственное решение: α = 2 , β = −3 , γ =1. Таким образом, с = 2 p −3q + r .

2.5. Скалярное произведение векторов

Определение. Скалярным произведением двух ненулевых векторов

a и b называется число (скаляр), равное произведению длин этих векторов на косинус угла между ними, т. е.

a b =		a				b		cosα ,	(2.16)
где α − угол между векторами a и b .
Если хотя бы один из векторов a или b									− нулевой, то угол между

векторами не определен, и скалярное произведение полагается равным нулю.

Проекцию вектора b на ось, определяемую вектором a , обозначим прab . По определению проекции вектора на ось имеем: прab = b cosα . Тогда

скалярное произведение двух ненулевых векторов a и b									определяется
формулой
a b =				a				прab .	(2.17)
Учитывая, что в определении скалярного произведения векторы a и
b взаимозаменяемые, его можно представить в виде
a b =			b					прba .	(2.18)
46

Соотношения (2.17) и (2.18) позволяют сформулировать другое определение скалярного произведения.

Определение. Скалярным произведением двух ненулевых векторов a и b называется число (скаляр), равное произведению длины одного из этих векторов на проекцию другого вектора на ось, определяемую первым из указанных векторов.

Физический смысл скалярного произведения заключается в следующем: если точка приложения силы, задаваемой постоянным вектором F , перемещается вдоль вектора a , то работа этой силы определяется равенст-

вом A = F a cosα , где α − угол между векторами a и F , т. е. работа равна

скалярному произведению векторов a и F .

Теорема 8. Необходимым и достаточным условием ортогональности (перпендикулярности) двух векторов является равенство нулю их скалярного произведения.

Доказательство. Необходимость. Пусть векторы a и b ортогональ-

ны, α − угол между ними, тогда cosα = 0 , и в силу формулы (2.16) a b = 0 . Достаточность. Пусть a b = 0 . Докажем, что векторы a и b ортогональны. Если хотя бы один из векторов равен нулевому вектору, то он имеет неопределенное направление, и можно считать, что векторы ортого-

нальны. Если оба вектора a и b ненулевые, то a 0 , b 0 , поэтому из

(2.16) следует, что cosα = 0 , т, е. векторы a и b ортогональны. Теорема доказана.

Если два вектора привести к общему началу, то в качестве угла α между этими векторами можно взять любой из углов ϕ1 или ϕ2 .

b

ϕ2	ϕ1	a

Действительно, сумма углов ϕ1 и ϕ2 равна 2π , поэтому cosϕ1 = cosϕ2 .

В определение скалярного произведения входит сомножителем только косинус угла между векторами. Из двух углов ϕ1 и ϕ2 между векторами один

всегда не более π . За угол α между векторами принимается наименьший

из углов ϕ1 и ϕ2 , т. е. α = min(ϕ1,ϕ2 ) .

Если скалярное произведение двух ненулевых неколлинеарных векторов a и b положительно (отрицательно), то эти два вектора составляют острый (тупой) угол.

Свойства скалярного произведения:

1. a b = b a .

47

Доказательство. Это свойство непосредственно вытекает из определения скалярного произведения: a b = a b cosα = b a cosα = b a . Свойство

доказано.

2. (λa) b = λ(a b) .

Доказательство. Для доказательства этого свойства воспользуемся формулой (2.18) для определения скалярного произведения и свойствами

проекций векторов на ось: (λa)b = b прb (λa) = λ b прba = λ(a b) . Свойство доказано.

3. (a +b) c = a c +b c .

Доказательство. Воспользуемся формулой (2.18) для определения скалярного произведения и свойствами проекций векторов на ось. Полу-

чим: (a +b) c = с прс(a +b) = с прсa + с прсb = a c +b c . Свойство доказано.

4. a a 0 , если a ≠ 0 , и a a =

0 , если a = 0.

Доказательство. Из определения скалярного произведения с ис-

пользованием соотношения (2.16)

следует, что

a a =

a

2 . Если a = 0, то

a

= 0 и a a = 0 . Если же a ≠ 0 , то

a

0 , поэтому

a a 0 . Свойство доказа-

но.

Эти свойства позволяют при скалярном перемножении векторных многочленов выполнять действия почленно, не учитывая порядок векторных сомножителей и сочетая числовые множители.

Из определения и свойств скалярного произведения векторов следует, что для базисных векторов i , j , k выполняются соотношения

a)	i i =		j j = k k =1;																															(2.19)
b)	i j =		j i =	j k = k j = k i = i k = 0 .																														(2.20)
Теорема 9. Если векторы a										и b							заданы своими координатами,																		т. е.
a = {X1,Y1,Z1},		b = {X2 ,Y2 ,Z2}, то скалярное произведение векторов a и b																																	вы-
числяется по формуле
				a b = X1X2 +YY1 2 + Z1Z2 .																														(2.21)
Доказательство. Разложим векторы a																							и b		по базису i ,								j , k , полу-
чим a = X1i +Y1 j + Z1k , b = X2i +Y2 j + Z2k .																			Тогда по							свойствам							скалярного
произведения векторов, используя формулы (2.19), (2.20), имеем																																		a b =
= (X i +Y j + Z k) (X				i +Y j + Z		k)		= X X					i 2			+			X Yi				j + X Z				i		k +YX		2	j i +YY j2 +
1	1	1	2	2	2					1	2								1		2				1	2			1				1	2
+YZ1 2 j k + Z1X2k i + Z1Y2k j + Z1Z2k2										= X1X2 +YY1 2 + Z1Z2 . Теорема доказана.
Следствие. Угол α					между ненулевыми векторами																									a = {X1,Y1,Z1} и
b = {X2 ,Y2 ,Z2} определяется по формуле
				cosα =					X X			2		+YY							+ Z Z			2				.						(2.22)
										1							1		2				1
							X	2		2	+ Z					2				X		2		2	+ Z	2
									+Y													2	+Y			2
						1				1					1									2

48

Доказательство. По определению скалярного произведения двух

ненулевых векторов a b =

a

b

cosα , поэтому cosα =

a

b

. Воспользовав-

a

b

шись формулами (2.21) и (2.9) для скалярного произведения и длин векторов, заданных своими координатами, получим формулу (2.22).

Замечание. Если один из векторов a или b является нулевым, то угол между векторами определяется неоднозначно и может быть выбран произвольным.

П р и м е р 24.

Дано, что

a

= 3 ,

b

= 5 . Определить, при каком значе-

нии α векторы a +αb

и a −αb

будут взаимно перпендикулярны.

Решение. Условием перпендикулярности векторов является равенст-

во нулю их скалярного произведения,

т. е.

(a +αb) (a −αb) = 0 . По свойст-

вам

скалярного

произведения

(a +αb) (a −αb) = a 2 −α2b 2

=

a

2 −α2

b

2 =

= 9 − 25α2 . Таким образом, 9 − 25α2

= 0, или α = ±3 .

5

π

П р и м е р 25. Векторы

a

и

b

образуют угол ϕ =

. Зная, что

6

a

=

3 ,

b

=1, вычислить угол α между векторами

p

= a

+b и q

= a −b .

Решение.

Для

нахождения

косинуса угла

α

между

векторами

и

воспользуемся

соотношением

(2.22).

По формуле

p = a +b

q = a −b

(2.21):

=

2

−

2

=

3 −1 = 2

. Найдем длины векто-

p

q

= (a +b) (a

−b)

= a 2

−b 2

a

b

ров

используя свойства скалярного произведения:

=

p

= a

+b и q

= a −b ,

p

π

2

=

p

=

p

p =

(a +b) (a

+b) = 3 +

2a b +1 =

4 + 2

3 1

cos 6

= 7 . Анало-

p

q

2

гично находим, что

q

=1. Тогда cosα =

=

и α = arccos

2

.

p

q

7

7

2.6. Векторное произведение векторов

Определение.

Тройка

векторов

называется

упорядоченной, если

указано, какой из векторов считается первым, какой − вторым, а какой − третьим.

Например, (b,a,c) − упорядоченная тройка векторов, в которой пер-

вым вектором является вектор b , вторым − вектор a , третьим − вектор c . Определение. Упорядоченная тройка некомпланарных векторов называется правой, если после приведения их к общему началу из конца третьего вектора кратчайший поворот от первого ко второму виден совершающимся против часовой стрелки. В противном случае тройка называет-

ся левой.

49

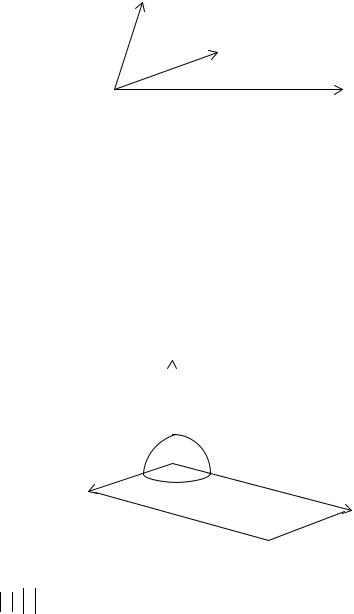
Определение. Тройка некомпланарных векторов a,b,c называется

правой (левой), если после приведения к общему началу векторы располагаются так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки.

c

b

a

Рассмотрим векторы a , b и c , расположенные таким образом, как показано на рисунке. Правыми тройками будут (a,b,c) , (b,c,a) и (c,a,b) .

Тройки векторов (b,a,c) , (a,c,b) , (c,b,a)

− левые.

Определение.

Векторным произведением вектора a

на вектор b

называется вектор a ×b , который определяется тремя условиями:

1)

длина вектора a ×b

равна

a

b

sinϕ , где ϕ − угол между векторами

a и b ;

вектор a ×b перпендикулярен каждому из векторов a

и b ;

2)

3)

векторы a , b

и a ×b образуют правую тройку.

a ×b

90°

90°

a

ϕ

S

b

Условия 2) и

3) относятся к

случаю, когда

a

b

sinϕ ≠ 0 . Если

a b sinϕ = 0 , то векторное произведение определяется только условием 1).

Определение. Декартова система координат называется правой (левой), если три базисных вектора образуют правую (левую) тройку.

Геометрические свойства векторного произведения.

Теорема 10. Для коллинеарности двух векторов необходимо и достаточно, чтобы равнялось нулю их векторное произведение.

Доказательство. Необходимость. Пусть векторы a и b коллинеар-

ны, тогда ϕ = 0 или ϕ = π и sinϕ = 0 . По определению векторного произве-

дения длина вектора a ×b равна		a				b		sinϕ = 0 , следовательно, векторное
произведение равно нулю.
	50

и (b,a,c)

(a,b,c)

неарен вектору и b . 3) Так как

Достаточность. Пусть a ×b = 0. Докажем, что векторы a и b коллинеарны. Если один из этих векторов, например вектор a , является нуле-

вым, то он коллинеарен любому вектору, в частности, и вектору b . Если оба вектора ненулевые, то a 0 , b 0 , поэтому из условия 1 скалярного

произведения следует, что sinϕ = 0 , т. е. векторы a и b коллинеарны. Теорема доказана.

Теорема 11. Длина (модуль) векторного произведения a ×b равняется площади параллелограмма, построенного на приведенных к общему на-

чалу векторах a и b .

Доказательство. Площадь параллелограмма равна произведению длин смежных сторон на синус угла между ними. Рассмотрим параллелограмм, построенный как на сторонах на приведенных к общему началу

векторах a и b . Тогда длины сторон равны a и b , угол между этими смежными сторонами равен углу ϕ между векторами. Поэтому площадь S параллелограмма равна S = a b sinϕ = a ×b . Теорема доказана.

Следствие. Если e − орт векторного произведения a ×b , а S − площадь параллелограмма, построенного на приведенных к общему началу

векторах a и b , то для векторного произведения a ×b	справедлива форму-
ла
a ×b = Se .	(2.23)

Доказательство. Проверим выполнение условий, которым должно удовлетворять векторное произведение a ×b , если a ×b = Se . 1) Длина ве к- торного произведения Se = S e = S = a b sinϕ = a ×b . 2) Вектор Se колли-

a ×b , поэтому он перпендикулярен каждому из векторов a S 0 , то вектор Se и вектор e , который является ортом векторного произведения a ×b , имеют одинаковое направление, следова-

тельно, векторы a , b и Se образуют правую тройку. Таким образом, вектор Se является векторным произведением векторов a и b , т. е. a ×b = Se . Следствие доказано.

Алгебраические свойства векторного произведения.

1. a ×b = −b ×a (свойство антиперестановочности сомножителей). Доказательство. Пусть c = a ×b , d = b ×a . Если векторы a и b кол-

линеарны, то по теореме 1 получаем, что с = d = 0 . Если векторы a и b не коллинеарны, то d = b a cosϕ = a b cosϕ = c , т. е. векторы c и d имеют

одинаковую длину. Векторы c и d коллинеарны, так как каждый из них перпендикулярен плоскости, в которой расположены векторы a и b , т. е. либо с = d , либо с = −d . Если векторы c и d равны, то тройки векторов одновременно являются обе правыми или левыми, что не-

возможно, следовательно, с = −d , или a ×b = −b ×a . Свойство доказано.

2. (λa) ×b = λ(a ×b) .

51

Доказательство. Пусть c = (λa) ×b , d = λ(a ×b) . Если векторы a и b коллинеарны или λ = 0 , то по теореме 1 получаем, что с = d = 0 .

Рассмотрим случай, когда векторы a

и b не коллинеарны и λ ≠ 0 .

Докажем, что в этом случае векторы c и d

равны. Пусть ϕ − угол между

векторами a

и b , а ψ − угол между векторами λa и b . Тогда

c

=

(λa) ×b

=

=

λa

b

sinψ

=

λ

a

b

sinψ ,

d

=

λ(a ×b)

=

λ

a ×b

=

λ

a

b

sinϕ

.

Если λ 0 ,

то векторы

a и λa направлены в одну сторону, поэтому ϕ =ψ и sinϕ =

= sinψ . Если же λ 0 , то векторы a и λa имеют противоположное направ-

ление, т. е. ψ = π −ϕ , но sinψ = sin(π −ϕ) = sinϕ . Таким образом, векторы c и

d имеют одинаковую длину при любых значениях λ . Векторы a , b и λa

расположены в одной плоскости, поэтому векторы c и d коллинеарны (оба перпендикулярны одной и той же плоскости). Для доказательства ра-

венства векторов c и d осталось доказать, что они одинаково направлены.

Действительно, если λ 0 (λ 0 ), то векторы a и λa одинаково (противо-
положно) направлены, поэтому векторы a ×b	и (λa) ×b , а также векторы
a ×b и λ(a ×b) одинаково (противоположно)	направлены. Следовательно,

векторы (λa) ×b	и λ(a ×b) имеют одинаковое направление. Свойство дока-
зано.

3. (a +b) ×c = a ×c +b ×c .

Доказательство. Если векторы a и b коллинеарны вектору c или

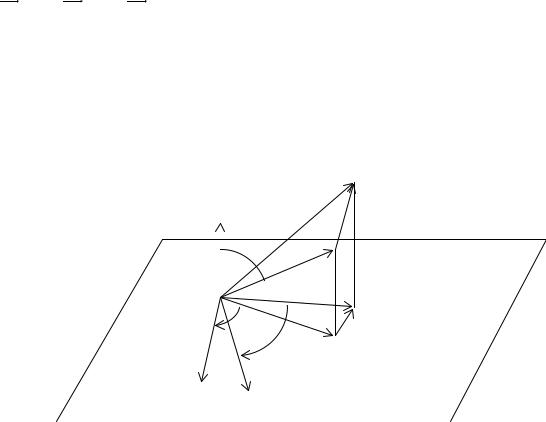
хотя бы один из векторов a , b , c нулевой, то свойство очевидно. Для доказательства свойства в других случаях введем орт с0 вектора c . Векторы

a и с0	приведем к общему началу O и через точку O проведем плоскость
π , перпендикулярную вектору с0 . Рассмотрим треугольник OAB такой, что
OA = a ,	AB = b , OB = a +b . Проекции точек A и B на плоскость π обозна-
чим A1	и B1 соответственно. Полученный треугольник OA1B1 повернем во-

круг оси, определяемой вектором с0 , на угол 90° по часовой стрелке, если смотреть из конца вектора с0 . Получим треугольник OA2B2 . Пусть ϕ − угол

между векторами с0	и a . Для определенности будем считать, что 0 ϕ					π
(для всех остальных случаев доказательство проводится аналогично).						2
	с0			a +b	В
			ϕ	a	b
					А
	О
					B1
					A1
	A2

52

π B2

Рассмотрим вектор OA2 .

Учитывая, что

c0

=1,

длину вектора OA2

можно представить в виде

OA2

=

OA1

=

a

cos(π

−ϕ)

=

a

sinϕ =

c0

a

sinϕ .

2

Вектор OA2 расположен в плоскости π , которая перпендикулярна вектору

с0 по построению, следовательно, OA2 с0 . Кроме того,

OA2 перпендикуля-

рен вектору a (по построению). Векторы a , с0 и OA2 образуют правую тройку. Таким образом, OA2 = a ×c0 . Проводя аналогичные рассуждения для

векторов OB2 и A2B2 , получим, что OB2		= (a +b) ×c0 ,	A2 B2 = b ×c0 . Учитывая,
что OB2 = OA2 +	+ A2B2 , получим:	+b ×c0 .
	(a +b) ×c0 = a ×c0		(2.24)
Вектор c	направлен так же, как и вектор с0 , поэтому c =				c		c0 . Ум-

ножим равенство (2.24) на число с . Получим с ((a +b) ×c0 ) = с (a ×c0 ) + + с (b ×c0 ) . Согласно алгебраическому свойству 2 векторного произведения (a +b) ×( с c0 ) = a ×( с c0 ) +b ×( с c0 ) или (a +b) ×c = a ×c +b ×c . Свойст-

во доказано.

4. a ×a = 0 для любого вектора a .

Доказательство. Любой вектор коллинеарен сам себе, поэтому по теореме 1 a ×a = 0 . Свойство доказано.

При доказательстве алгебраического свойства 3 использовалось следствие из свойства 2.

Следствие 1. a ×(λb) = λ(a ×b) .

Доказательство. Для доказательства этого утверждения воспользуемся свойством антиперестановочности сомножителей векторного произ-

ведения и свойством 2. Имеем: a ×(λb) = −(λb) ×a = −λ(b ×a) = λ(a ×b) . Следствие доказано.

Следствие 2. c ×(a +b) = c ×a + c ×b .

Доказательство. Воспользуемся свойством антиперестановочности сомножителей векторного произведения и свойством 3. Имеем: c ×(a +b) =

= −(a +b) ×c = −(a ×c +b ×c) = −a ×c −b ×c = c ×a + c ×b . Следствие доказано.

Используя следствия 1 и 2, получим:

(αa + βb) ×(λc + µd ) =αλa ×c +αµa ×d + βλb ×c + βµb ×d .

(2.25)

2.7. Выражение векторного произведения через координаты векторов

Из определения и свойств скалярного произведения векторов следует, что для базисных векторов i , j , k выполняются соотношения

53