Analiticheskaya_Geometria

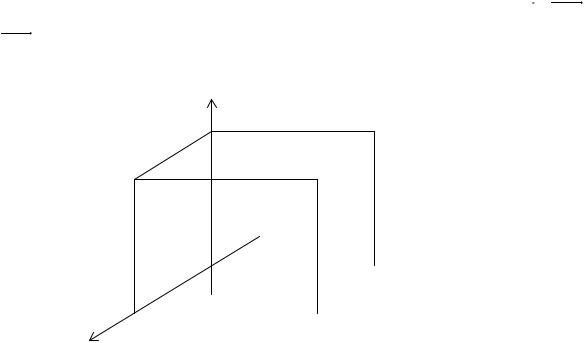
Теорема 7. Пусть в прямоугольной системе координат задано общее уравнение линии второго порядка Ax2 + 2Bxy +Cy2 + 2Dx + 2Ey + F = 0 . Тогда

существует такая прямоугольная система координат, в которой это уравнение принимает один из следующих канонических видов:

	1)		x2	+		y2		=1 − эллипс;
			a2			b2
	2)		x2	+	y2			= −1 − мнимый эллипс;
			a2
						b2

3) a2 x2 +b2 y2 = 0 – пара мнимых пересекающихся прямых;

	4)	x2	−	y2	=1 – гипербола;
		a2		b2

5)a2 x2 −b2 y2 = 0 – пара пересекающихся прямых;

6)y2 = 2 px – парабола;

7)y2 − a2 = 0 – пара параллельных прямых;

8)y2 + a2 = 0 – пара мнимых параллельных прямых;

9)y2 = 0 – пара совпадающих прямых.

2.ВЕКТОРНАЯ АЛГЕБРА

2.1. Декартовы координаты в пространстве

Три взаимно перпендикулярные оси в пространстве (координатные оси) с общим началом O и одинаковой масштабной единицей образуют декартову прямоугольную систему координат в пространстве. Обозначим оси Ox , Oy и Oz . Точка O называется началом системы координат, оси Ox ,

Oy и Oz − осями абсцисс, ординат и аппликат. Пусть Mx , My , Mz − проек-

ции произвольной точки M пространства на оси Ox , Oy и Oz соответст-

венно.

Определение. Декартовыми прямоугольными координатами x , y , z точки M называются величины направленных отрезков OMx , OMy и

OMz . Декартовы координаты x , y и z точки M называются соответст-

венно ее абсциссой, ординатой и аппликатой.

z

Mz

M

О	My	y
	34

Mx

x

То, что точка M имеет координаты x , y и z , символически обозначают M(x, y, z) . Таким образом, при выбранной системе координат каждой

точке M пространства соответствует единственная упорядоченная тройка чисел (x, y, z) , и каждой упорядоченной тройке чисел (x, y, z) соответствует

единственная точка M в пространстве.

Попарно взятые координатные оси располагаются в координатных плоскостях Oxy , Oxz, Oyz. Эти плоскости разбивают пространство на во-

семь частей, называемых октантами.

2.2. Векторы. Линейные операции над векторами

Определение. Вектором называется направленный отрезок AB с начальной точкой A и конечной точкой B .

В

AB

А

Начало вектора называют точкой приложения вектора. Иногда вектор обозначают одной латинской буквой, например a .

Определение. Длиной (или модулем) вектора AB называется длина

отрезка

AB

, т. е. записи

AB

и

a

обозначают длины векторов AB и a со-

ответственно.

Если

AB

=1, то вектор

AB называется единичным. Если начало и

конец вектора совпадают, например AA, то такой вектор называется нуле-

вым и обозначается 0 = AA. Нулевой вектор не имеет определенного направления, и его длина равна нулю. Поэтому при записи нулевой вектор можно отождествлять с вещественным числом 0.

Определение. Векторы называются коллинеарными, если они лежат на одной или параллельных прямых.

Нулевой вектор коллинеарен любому вектору.

Определение. Векторы называются равными, если они имеют одинаковую длину и одинаковое направление. Все нулевые векторы считаются равными.

35

Из определения равенства векторов следует, что каковы бы ни были вектор a и точка P , существует единственный вектор PQ с началом в точке P , равный вектору a .

Другими словами, точка приложения данного вектора a может быть выбрана произвольно, поэтому геометрические векторы называются свободными.

Определение. Единичный вектор, имеющий одинаковое направление с вектором a , называется ортом вектора a и обозначается обычно

символом a0 .

Линейными операциями над векторами принято называть операцию сложения векторов и операцию умножения векторов на вещественные числа.

Определение. Суммой a +b двух векторов a и b называется вектор c , начало которого совпадает с началом вектора a , а конец − с концом вектора b при условии, что вектор b приложен к концу вектора a .

a	b

a +b

Этот способ сложения векторов называется правилом треугольника. Операция сложения векторов обладает следующими свойствами.

1. a +b = b + a .

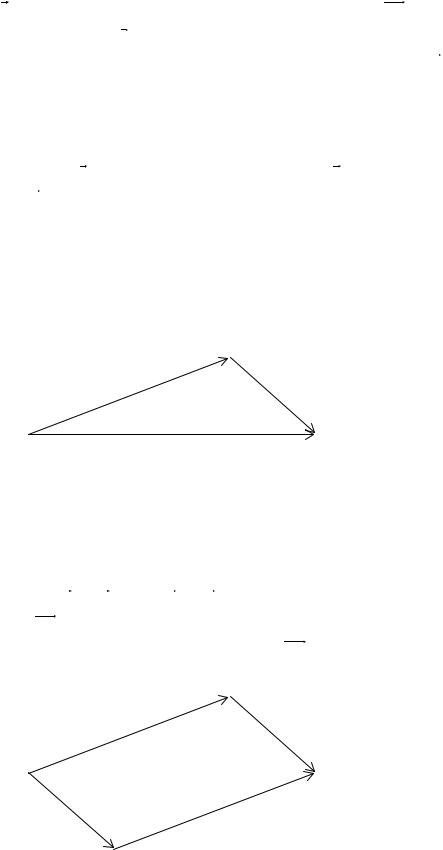
Доказательство. Приложим два произвольных вектора a и b к общему началу O . Обозначим концы векторов a и b буквами A и B соответственно и рассмотрим параллелограмм OBCA. Из равенства векторов

следует, что BC = OA = a , AC = OB = b . Из треугольника OAC следует, что диагональ OC рассматриваемого параллелограмма равна a +b , из тре-

угольника OBC получаем, что диагональ OC равна b + a . Таким образом,
a +b = b + a . Свойство доказано.			B
		a	b
О		a +b		C
	b	A	a

2. (a +b) + c = a + (b + c) .

36

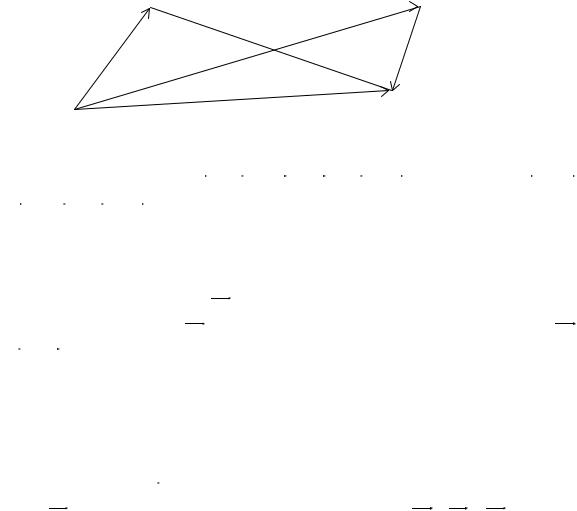
Доказательство. Для доказательства этого свойства приложим вектор a к произвольной точке O , вектор b − к концу вектора a , а начало вектора c совместим с концом вектора b .

	A							B
			b + c	b
					a +b		c
	a
О						C
		(a	+b) + c	= a + (b + c)
Обозначим буквами A, B и C					концы векторов a , b и c соответст-
венно и рассмотрим четырехугольник OABC .
Тогда	(a +b) + c = (OA+ AB) + BC = OB + BC = OC ,							a + (b + c) = OA+ (AB +

+BC) = OA+ AC = OC , т. е. (a +b) + c = a + (b + c) . Свойство доказано.

3.Существует нулевой вектор 0 такой, что для любого вектора a

выполняется равенство a + 0 = a .

Доказательство. Обозначим буквами A и B соответственно начало

иконец вектора a , т. е. a = AB . Приложим начало нулевого вектора к кон-

цу вектора a , тогда 0 = BB. По определению суммы векторов a + 0 = AB +

+BB = AB = a . Свойство доказано.

4.Для каждого вектора a существует противоположный ему вектор

a′ такой, что a + a′ = 0 .

Доказательство. Определим вектор a′ как вектор, коллинеарный вектору a , имеющий с вектором a одинаковую длину и противоположное направление. Обозначим буквами A и B соответственно начало и конец

вектора a , т. е. a = AB . Приложим начало вектора a′ к концу вектора a , то-

гда a′ = BA. По определению суммы векторов a + a′ = AB + BA = AA = 0 . Свойство доказано.

Доказательство свойства 1 позволяет вывести правило параллелограмма для сложения двух векторов: если векторы a и b приложены к общему началу и на них, как на смежных сторонах, построен параллело-

грамм, то сумма a +b (или b + a ) этих векторов представляет собой диагональ построенного параллелограмма, идущую из общего начала векторов

a и b .

Если векторы a и b коллинеарны, то параллелограмм, построенный на этих векторах, как на сторонах, вырождается в отрезок, поэтому понятие диагонали параллелограмма теряет смысл, и сложение векторов осуществляется по правилу треугольника.

Доказанные свойства операции сложения векторов совпадают со свойствами операции сложения действительных чисел. Поэтому правило сложения можно распространить на сумму любого конечного числа векторов. Сумма любого числа векторов может быть построена по правилу

37

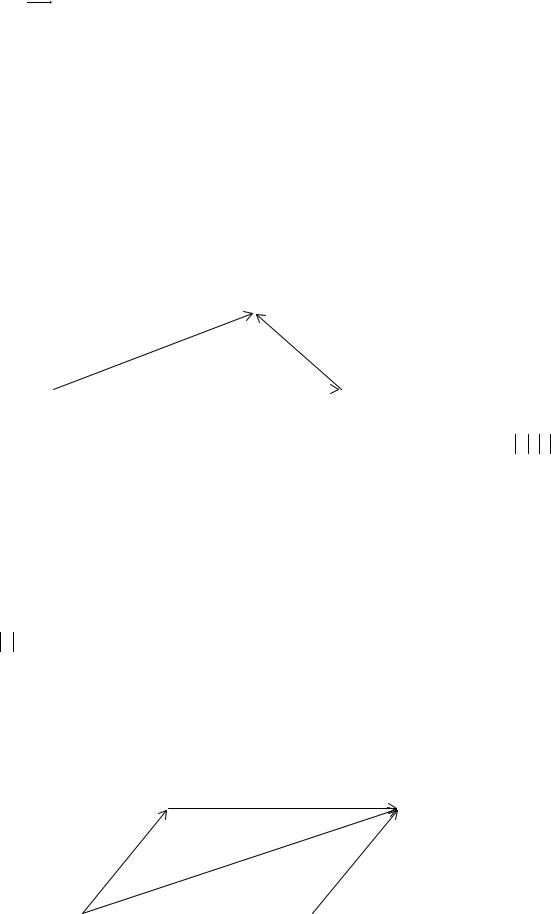
многоугольника: чтобы сложить несколько векторов a1 , a2 , …, ak , надо вектор ai (i = 2, 3,...,k ) приложить к концу вектора ai−1 , тогда суммой векторов a1 + a2 +... + ak будет вектор, соединяющий начало вектора a1 с концом вектора ak .

Если O − начало вектора a1 , Ai − конец вектора ai (i = 2,3,...,k ), то

вектор OAk замыкает ломаную OA1 A2...Ak до многоугольника, поэтому пра-

вило сложения векторов по правилу многоугольника иногда называют

правилом замыкания ломаной до многоугольника.

Определение. Разностью a −b векторов a и b		называется вектор c ,
который в сумме с вектором	b дает вектор a .	и b	, где b		− вектор,
Покажем, что вектор c	равен сумме векторов a
противоположный вектору b . Действительно, если c		′		′
		= a +b , то по свойст-
				′	+ (b +b) =
вам 2 − 4 операции сложения векторов имеем: с +b = (a +b ) +b = a
			′		′

= a + 0 = a , т. е. вектор c равен разности векторов a и b .

Из определения разности и правила треугольника сложения векторов следует правило построения разности a −b : разность a −b приведенных к общему началу двух векторов a и b представляет собой вектор, идущий из конца вычитаемого вектора b к концу уменьшаемого вектора a .

a	a −b
	b

Определение. Произведением λa вектора a на вещественное чис-

ло λ называется вектор, коллинеарный вектору a , имеющий длину λ a и

направление, совпадающее с направлением вектора a в случае λ 0 и противоположное направлению вектора a в случае λ 0 . Если λ = 0 или a = 0, то произведение λa равно нулевому вектору, направление которого не определено.

Таким образом, при умножении вектора на число происходит его

	«растяжение»	в		λ раз, т. е. он либо растягивается в λ раз (λ 1), либо
	сжимается в	1		раз (0 λ 1), либо кроме растяжения (		λ		1) и сжатия
		λ

(0 λ 1) происходит изменение направления вектора.

Свойства операция умножения вектора на вещественное число:

1. Распределительное свойство числового сомножителя относительно суммы векторов: λ(a +b) = λa + λb .

Доказательство. Приложим векторы a и b к общему началу O и на них, как на смежных сторонах, построим параллелограмм, диагональ которого будет равна a +b .

λb	λ(a +b)
	38

b

a +b

О

a

λa

При «растяжении» сторон этого параллелограмма в λ раз в силу

свойств подобия диагональ также «растягивается» в λ

раз. Это означает,

что λa + λb = λ(a +b) . Свойство доказано.

2. Распределительное свойство векторного сомножителя относитель-

но суммы чисел: (λ + µ)a = λa + µa .

Доказательство. Если a = 0, то по определению умножения вектора

на число (λ + µ)a = 0 , λa = 0 , µa = 0 и, следовательно, (λ + µ)a = λa + µa .

Если λ = 0 или µ = 0 , то справедливость равенства следует из свойств

вещественных чисел и определения умножения вектора на число.

Пусть числа λ и µ имеют одинаковые знаки и a ≠ 0 . Тогда векторы

(λ + µ)a , λa

и µa

(соответственно и векторы (λ + µ)a ,

λa + µa ) коллинеар-

ные

и

одинаково

направлены.

Поэтому

λa + µa

=

λa

+

µa

=

=

λ

a

+

µ

a

= (

λ

+

µ

)

a

. Если числа λ и µ имеют

одинаковые знаки,

то

λ + µ

=

λ

+

µ

, поэтому

(λ + µ)a

=

λ + µ

a

= (

λ

+

µ

)

a

. Таким образом,

векторы (λ + µ)a

и λa + µa

коллинеарные, одинаково направлены и имеют

равные длины, следовательно, они равны.

Пусть числа λ и µ имеют разные знаки и a ≠ 0 . Для определенности будем считать, что λ µ . В этом случае векторы (λ + µ)a и λa + µa на-

правлены так же, как и вектор λa . Длина вектора (λ + µ)a равна (λ + µ)a =

=

λ + µ

a

= (

λ

−

µ

)

a

, а для вектора λa + µa имеем:

λa + µa

=

λa

−

µa

=

=

λ

a

−

µ

a

= (

λ

−

µ

)

a

, т. е. длины векторов (λ + µ)a

и λa + µa равны.

Так как эти векторы коллинеарные, направлены в одну сторону и имеют одинаковые длины, то они равны.

Если λ = −µ , то обе части доказываемого равенства равны нулю, следовательно, (λ + µ)a = λa + µa . Свойство доказано.

3. Сочетательное свойство числовых сомножителей: λ(µa) = (λµ)a . Доказательство. Если λµ = 0 или a = 0, равенство верно, так как обе

части равенства обращаются в нуль. Если λ ≠ 0 , µ ≠ 0 , a ≠ 0 , то направления векторов λ(µa) и (λµ)a либо совпадают с направлением вектора a (ес-

ли λµ 0 ), либо противоположны направлению

вектора a (если λµ 0 ),

т. е. векторы λ(µa) и (λµ)a одинаково направлены. Кроме того,

они имеют

одинаковые длины:

λ(µa)

=

λ

µa

=

λ

µ

a

и

(λµ)a

=

λµ

a

=

λ

µ

a

.

Следовательно, векторы λ(µa) и (λµ)a

равны. Свойство доказано.

2.3. Проекции векторов

39

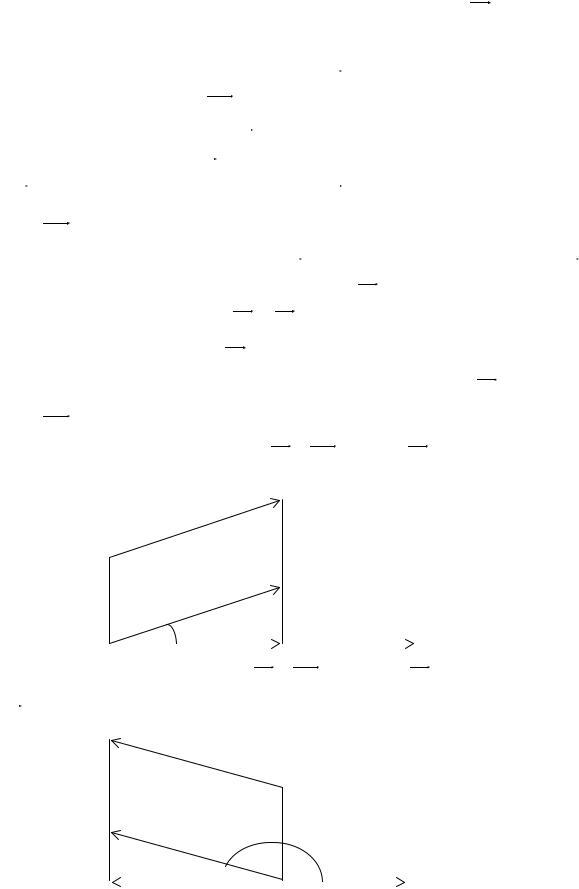
Пусть в пространстве задана некоторая ось l и вектор AB . Через точки A и B проведем плоскости, перпендикулярные прямой l. Обозначим

точки пересечения прямой и построенных плоскостей A и

B .

′

′

AB

Определение. Проекцией вектора AB на ось l называется величина

направленного отрезка AB

на оси l , т. е.

′ ′

′ ′

(2.1)

прl

AB = AB .

′ ′

Если направление AB совпадает с направлением оси l, то AB =

′ ′

′

′

=

AB

, если же направления

вектора AB

и

оси противоположны,

то

′

′

′ ′

.

′ ′

= −

′ ′

AB

AB

Теорема 1. Проекция вектора AB на ось l

равна длине вектора

AB ,

умноженной на косинус угла между вектором AB и осью l, т. е.

прl AB =

AB

cosϕ ,

(2.2)

где ϕ − угол между вектором AB и осью l .

Доказательство. Если ϕ = π2 , то при проекции вектора AB на ось l вектор A′B′является нулевым, поэтому условие (2.2) выполняется.

Если ϕ	π	, то в силу (2.1)	′ ′		′ ′		=		AB		cosϕ .
	2		прl AB = AB =		AB
			B
А

′

ϕ

′

l

A

B

Если же ϕ

π

′ ′

= −

′ ′

= −

AB

cos(π −ϕ) =

2 , то в силу (2.1)

прl AB = AB

AB

=

AB

cosϕ .

B

А

ϕ

l

′

′

B

A

40

Пусть задана некоторая ось l и

A1B1

= A2B2 . Применяя к каждому из

этих векторов формулу (2.2),

получим,

что прl A1B1 = прl A2B2 ,

т. е. равные

векторы имеют равные проекции на одну и ту же ось.

Определение.

Проекции

X = прOx AB , Y = прOy AB ,

Z = прOz AB вектора

AB на оси Ox , Oy и Oz прямоугольной системы координат Oxyz называ-

ются координатами вектора AB в этой системе координат.

Если для вектора AB X = прOx AB , Y = прOy AB ,

Z = прOz AB, то символи-

чески это записывается в виде

AB = {X,Y,Z}.

(2.3)

Теорема 2. Для любых двух точек A(x1, y1, z1)

и B(x2 , y2 , z2 ) координаты

вектора AB определяются по формулам

X = x2 − x1 , Y = y2 − y1 ,

Z = z2 − z1 .

(2.4)

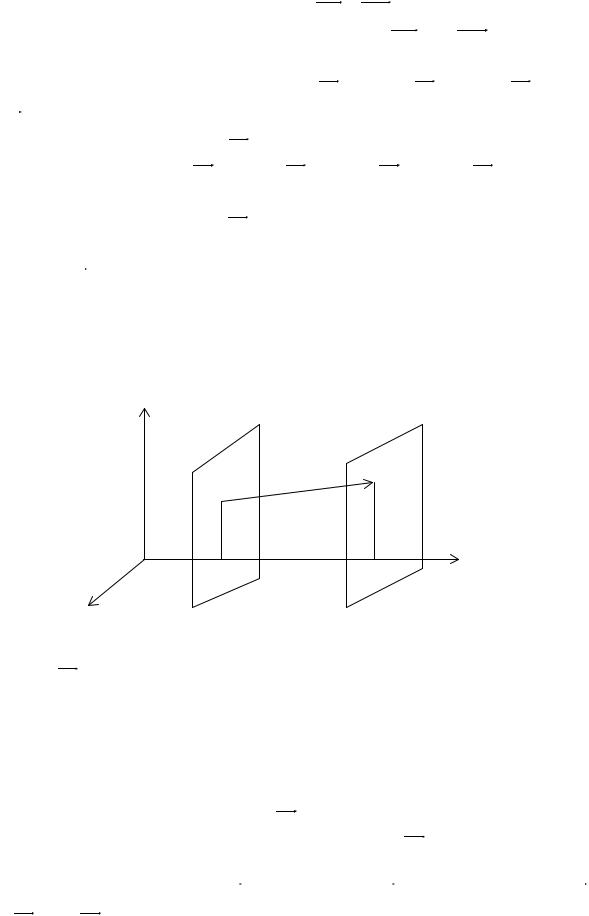
Доказательство. Проведем через точки A и B плоскости, перпенди-

кулярные оси Oy ,

и обозначим точки пересечения оси Oy и построенных

плоскостей

′

и

′

A

B .

z

A

B

′

y

O

A

′

B

x

y1

y2

Точки

′

и

′

имеют на оси Oy координаты y1 и y2 . По определению

A

B

Y

′

′

но

′ ′

− y1 . Аналогично доказываются

= прOy AB = AB ,

AB = y2 − y1 , т. е. Y = y2

и остальные соотношения. Теорема доказана.

Рассмотрим свойства проекций векторов на ось.

Теорема 3. Проекция суммы двух векторов на ось равна сумме их

проекций на эту ось, т. е.

прl (a +b) = прla + прlb .

(2.5)

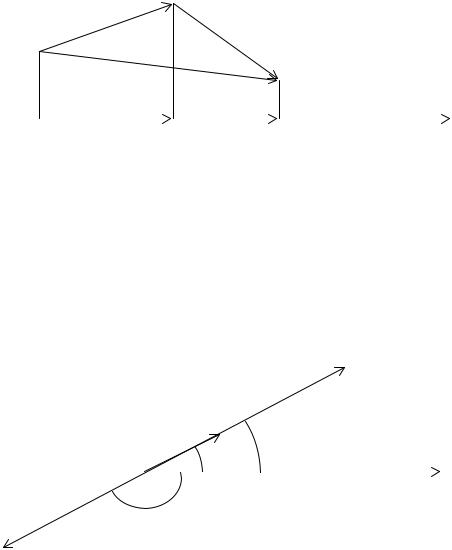
Доказательство. Пусть

a = AB ,

тогда, приложив вектор b

к концу

′

вектора a , т. е. к точке B , можем считать, что b = BC . Обозначим через A ,

′

, C

′

проекции точек A, B и С на ось l. По определению проекции векто-

B

ра на ось имеем:

′ ′

′

прl (a +b) =

прl (AB +

прla = прl AB = AB ,

прlb = прl BC = B C ,

′

′

,

′ ′

′

′

=

′

′

(последнее равенство сле-

+ BC) = прl AC = AC

прla + прlb = AB + B C

AC

дует из правила сложения величин вещественных чисел).

41

B

a		b
A	a +b			C
′	′	C	′	l
A	B

Таким образом, прl (a +b) = прla + прlb . Теорема доказана.

Теорема 4. При умножении вектора a на число λ его проекция на

ось также умножается на это число, т. е.

прl (λa) = λпрla .

(2.6)

Доказательство. Пусть ϕ − угол между осью l

и вектором a , а ϕ′ −

угол между осью l и вектором λa . Если λ 0 , то векторы a

и λa направ-

лены одинаково и ϕ = ϕ′. Если же λ 0 ,

то векторы a

и λa

имеют проти-

воположное направление и ϕ′ = π −ϕ .

λa, λ 0

a

ϕ′

l

ϕ

ϕ′

λa, λ 0

Согласно

(2.2) при λ 0 имеем:

прl (λa) =

λa

cosϕ = λ

a

cosϕ = λпрla .

Если же λ 0 ,

то прl (λa) =

λa

cos(π −ϕ) = −λ

a

cos(π −

ϕ)

= λ

a

cos

ϕ

= λпрla . При

λ = 0 обе части равенства (2.6) обращаются в нуль. Таким образом, прl (λa) = λпрla при любых вещественных значениях λ . Теорема доказана.

Из этой теоремы вытекает следствие.

Следствие. Если векторы a и b заданы своими координатами, т. е.

a = {X1,Y1,Z1},	b = {X2 ,Y2 ,Z2}, то при любых действительных числах	λ и µ
вектор λa + µb	имеет координаты
	λa + µb = {λX1 + µX2 , λY1 + µY2 , λZ1 + µZ2}.	(2.7)

Пусть α, β, γ − углы наклона вектора a к осям Ox , Oy и Oz соответ-

ственно.

Определение. Три числа cosα , cos β и cosγ называются направ-

ляющими косинусами вектора a .

Из определения координат вектора следует, что если a = {X,Y,Z}, то

42

Так как a

X =

a

cosα , Y =

a

cos β ,

Z =

a

cosγ .

(2.8)

является диагональю прямоугольного параллелепипеда со

сторонами, которые отсекают на координатных осях величины X ,

Y и Z ,

то

a

.

(2.9)

=

X2 +Y2 + Z2

Из формул (2.8) и (2.9) находятся выражения для направляющих ко-

синусов вектора a

через его координаты:

cosα =

X

, cos β =

Y

, cosγ =

Z

.

(2.10)

X

2

2

2

X

2

2

2

X

2

2

2

+Y + Z

+Y + Z

+Y + Z

Возводя полученные равенства в квадрат и складывая, получим, что

cos2 α + cos2 β + cos2 γ =1,

т. е. сумма квадратов направляющих

косинусов

любого вектора равна единице.

Так как вектор a

однозначно определяется заданием трех его коор-

динат, из полученных формул (2.8) следует, что вектор a однозначно определяется заданием его длины и трех направляющих косинусов.

П р и м е р 22. Даны два вектора a = {3, − 2, 6} и b = {− 2,1, 0}. Найти

проекции на координатные оси векторов a −b и 2a +3b .

Решение. Проекциями вектора на координатные оси являются его координаты. По формуле (2.7) получим: a −b = {3 −(−2), − 2 −1, 6 - 0}= {5, −3, 6},

2a +3b = {2 3 +3 (− 2), 3 (− 2) +3 1, 2 6 +3 0}= {0, −3,12}.

2.4. Разложение вектора по базису

Пусть i , j , k − единичные векторы осей координат, т. е. i = j = = k =1, и каждый из них одинаково направлен с осями Ox , Oy и Oz соот-

ветственно. Векторы i , j , k называются базисными векторами. Они взаимно перпендикулярны и задаются координатами следующим образом:

i = {1, 0, 0}, j = {0,1, 0}, k = {0, 0,1}.

Теорема 5. Любой вектор a может быть единственным образом раз-

ложен по базису i , j , k , т. е. представлен в виде
		a = λi + µj +νk ,		(2.11)
где λ,µ,ν − действительные числа.
Доказательство. Рассмотрим вектор OM = a .
z		Mz
		M
О
Mx			My	y
	43