Analiticheskaya_Geometria

		i ×i = 0 ,		i × j = k , i ×k = − j ,										j × j = 0 ,								j ×k = i ,												k ×k = 0 .																	(2.26)
		Теорема 12. Если векторы a														и b заданы своими координатами,																																				т. е.
a = {X1,Y1,Z1},			b = {X2 ,Y2 ,Z2}, то векторное произведение векторов a																																															и b		вы-
числяется по формуле
										Y	Z			,		Z	X		,		X					Y			,																						(2.27)
					a	×b		=		1		1				1	1					1			1
										Y2 Z2						Z2 X2					X2 Y2
или a ×b = {YZ1 2 − Z1Y2 , Z1 X2 − X1Z2 , X1Y2 −Y1 X2}.
		Доказательство. Разложим векторы a																								и b					по базису i ,																	j , k , полу-
чим	a = X1i +Y1 j + Z1k ,					b = X2i +Y2 j + Z2k .															Тогда								по					свойствам														векторного
произведения векторов, используя формулы (2.26), имеем:																																														a ×b = (X1i +
+Y j + Z k) ×(X				i +Y j + Z			k) = X X					i		×i +			X Yi					× j +						X Z						i ×k +YX										2	j ×i +YY j × j +
1		1	2		2	2		1			2						1		2										1		2							1												1	2
+YZ	2	j ×k + Z X			k ×i + Z Yk × j + Z Z										k ×k = (YZ									2		− Z Y )i + (Z												X		2		−			X Z				)j + (X Y −
1			1	2		1	2				1		2								1							1		2							1								1	2					1	2
−Y1 X2 )k = {YZ1			2 − Z1Y2 , Z1 X2 − X1Z2 , X1Y2 −Y1 X2} =																							Y		Z				,		Z		X			,		X				Y					Теорема
																										1				1				1		X	1					1			1			.
																										Y Z								Z							X				Y
																										2				2					2		2						2		2

доказана.

Следствие. Если векторы a = {X ,Y,Z }

1 1 1

то их координаты пропорциональны, т. е.

	X			Y		Z
		1	=	1	=		1	.
	X	2		Y		Z	2
				2
Доказательство. Если векторы a и b
формулы (2.27) получаем, что YZ1					2 − Z1Y2 = 0 ,

и b = {X2 ,Y2 ,Z2} коллинеарны,

(2.28)

коллинеарны, то a ×b = 0. Из

Z X − X Z = 0, X Y −YX = 0.

1 2 1 2 1 2 1 2

Из этих равенств следует (2.28). Следствие доказано.

Соотношения (2.28) называются условием параллельности (коллинеарности) двух векторов.

Следствие. Если векторы a и b

заданы своими координатами, т. е.

a = {X1,Y1,Z1},

b = {X2 ,Y2 ,Z2}, то векторное произведение векторов a и b вы-

числяется по формуле

i

j

k

a ×b

.

(2.29)

=

X1

Y1

Z1

X2

Y2 Z2

i

j

k

Доказательство. Разложим определитель

по первой стро-

X1

Y1

Z1

i

j

k

X2

Y2

Z2

ке, получим

= (YZ1

+ (Z1 X2 − X1Z2 )j +

(X1Y2 −Y1 X2 )k =

X1

Y1

Z1

2 − Z1Y2 )i

X2 Y2 Z2

= {YZ1 2 − Z1Y2 , Z1 X2 − X1Z2 , X1Y2 −YX1 2}= a ×b .

54

П р и м е р 26. Известно, что				a		=10 ,		b		= 2 и a b =12 . Найти длину
векторного произведения векторов a				и b .
Решение.	По	определению						векторного			произведения

a ×b = a b sinα , где α − угол между векторами. По формуле (2.22) име-

ем: cosα =

a b

=

12

=

3

. Учитывая, что угол между векторами не превы-

10 2

5

шает

a

b

π ,

из

основного

тригонометрического

тождества

получим:

4

. Таким образом,

4

sinα =

1−cos

2

=10 2

α =

5

a

×b

5 =16 .

П р и м е р 27. Даны точки A(1, 2, 0) , B (3, 0, −3)

и C (5, 2, 6) . Вычислить

площадь S треугольника ABC .

Решение. Площадь S треугольника ABC равна половине площади S1

параллелограмма,

построенного на векторах AB и AC , т. е. S =

1

AB× AC

.

2

Согласно (2.4)

AB = {2, − 2, −3}, AC = {4, 0, 6}, поэтому по формуле (2.29) име-

ем: AB× AC =

i

j

k

= {−12, − 24, 8}. Тогда S = 1

=14 .

2

− 2 −3

(−12)2 + (−24)2 +82

4

0

6

2

П р и м е р 28. Найти вектор p , зная, что он перпендикулярен векто-

и b

7k) =10 .

рам a = {2, −3,1}

= {1, − 2, 3} и удовлетворяет условию p (i + 2 j −

Решение. Пусть вектор

p имеет координаты {X, Y, Z}. Тогда условие

2 j −7k) =

10

можно записать в виде X + 2Y −7Z =10 . Вектор p пер-

p (i +

пендикулярен векторам a и b , поэтому он коллинеарен вектору a ×b . По

формуле (2.29)

a ×b =

i

j

k

= {−7, −5, −1}. Условие коллинеарности век-

2

−3

1

1

− 2

3

X

Y

Z

торов p и a ×b

согласно (2.28) имеет вид

=

=

. Поэтому для неиз-

−7

−5

−1

X + 2Y −7Z =10

вестных X, Y, Z получили систему уравнений

X

Y

Z , решив ко-

=

=

−7

−5

−1

торую найдем, что p = {7, 5,1}.

2.8. Смешанное произведение трех векторов

Пусть даны три произвольных вектора a , b и c .

Определение. Смешанным произведением трех векторов a , b , c

называется скалярное произведение вектора a на векторное произведение векторов b и c , т. е.

abc = a (b ×c) .	(2.30)
55

56

Геометрический смысл смешанного произведения раскрывает следующая теорема.

Теорема 13. Смешанное произведение a (b ×c) равно объему параллелепипеда, построенного на приведенных к общему началу векторах a , b и c , взятому со знаком плюс, если тройка векторов (a,b,c) правая, и со знаком минус, если тройка (a,b,c) левая. Если же векторы a , b и c компланарны, то a (b ×c) = 0.

Доказательство. Если векторы b и c коллинеарны, то векторы a , b и c компланарны. Для компланарных векторов b и c по свойству векторного произведения b ×c = 0 , поэтому по свойству скалярного произведения a (b ×c) = a 0 = 0 , т. е. для компланарных векторов теорема доказана.

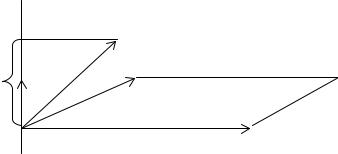
Пусть векторы a , b и c не компланарны. Приведем эти векторы к общему началу O . По формуле (2.23) b ×с = Se , где S − площадь параллелограмма, построенного на приведенных к общему началу векторах b и c , e − орт векторного произведения b ×c . Тогда

a (b ×с) = Sa e = S прea .

(2.31)

Проекция вектора a на ось, определяемую вектором e , с точностью до знака равна высоте h параллелограмма, построенного на приведенных к общему началу векторах a , b и c , при условии, что основанием служит параллелограмм, построенный на векторах b и c .

		a
h	e	c
		b
		О

Таким образом, правая часть равенства (2.31) с точностью до знака равна объему параллелепипеда, построенного на векторах a , b и c . Если векторы e и a лежат по одну сторону от плоскости, определяемой векто-

рами b и c , то прea = h , если же векторы e	и a	лежат по разные стороны
от этой плоскости, то прea = −h . Векторы b ,	c и e	образуют правую тройку
по определению векторного произведения	b ×c , таким образом, прea = h ,

если векторы b ,	c и a (соответственно векторы a ,	b и c ) образуют пра-
вую тройку, и прea = −h , если тройка векторов (a,b,c)		левая.
Если векторы a , b и c компланарны, то вектор a лежит в плоскости
векторов b и c ,	следовательно, прea = 0 , и a (b ×с) = Sa e = S прea = 0 . Тео-
рема доказана.

Из этой теоремы следует, что объем параллелепипеда, построенного

на приведенных к общему началу векторах a , b и c , вычисляется по формуле

V = mod(a (b ×c)) .	(2.32)
Следствие 1. Для любых трех векторов a , b и c справедливо равен-
ство
(a ×b) c = a (b ×c) .	(2.33)
Доказательство. Из переместительного свойства скалярного произ-
ведения следует a (b ×c) = (b ×c) a , поэтому достаточно	доказать, что

(a ×b) c = (b ×c) a . Последнее равенство выполняется с точностью до знака, потому что обе его части с точностью до знака определяют объем параллелепипеда, построенного на векторах (a ×b) c = a (b ×c) . Но тройки векторов (a,b,c) и (b,c,a) одновременно являются либо правыми, либо левыми, следовательно, знаки выражений (a ×b) c и (b ×c) a совпадают. Таким образом, (a ×b) c = (b ×c) a = a (b ×c) . Следствие доказано.

Доказанное равенство (2.33) позволяет записывать смешанное про-

изведение трех векторов a , b и c просто в виде abc , без указания при этом, какие два вектора (первые два или последние два) перемножаются векторно.

Следствие 2. Три вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю.

Доказательство. Если векторы компланарны, то, согласно доказанной теореме, их смешанное произведение равно нулю. Если смешанное произведение векторов равно нулю, то по этой же теореме проекция одного из векторов на ось, определяемую векторным произведением двух других векторов, равна нулю, т. е. он параллелен плоскости, в которой лежат два другие вектора. Это означает, что векторы компланарны. Следствие доказано.

Следствие 3. Смешанное произведение трех векторов, два из которых совпадают, равно нулю.

Доказательство. Если два вектора из трех совпадают, то такие три вектора компланарны и их смешанное произведение равно нулю. Следст-

вие доказано.
Теорема 14. Если векторы a , b				и с заданы своими координатами, т.
е. a = {X1,Y1,Z1}, b = {X2 ,Y2 ,Z2}, с = {X3,Y3,Z3}, то							смешанное произведение
векторов a , b и с вычисляется по формуле
abс =		X1 Y1 Z1				.	(2.34)
		X2	Y2	Z2
		X3	Y3	Z3

57

Доказательство. Разложим определитель, стоящий в правой части

выражения (2.34), по первой строке. Получим:		X1 Y1 Z1
		X2	Y2	Z2		= X1(Y2Z3 −
		X3	Y3	Z3

− Z2Y3 ) + Y1(Z2 X3 − X2Z3 ) + Z1(X2Y3 −Y2 X3 ) = a {Y2Z3 − Z2Y3, Z2 X3 − X2Z3, X2Y3 −Y2 X3}=

= a (b ×c) = abc . Теорема доказана.

Теорема 15. Пусть даны точки

A(x1, y1, z1) , B(x2 , y2 , z2 ) ,

C(x3, y3, z3 ) ,

D(x4 , y4 , z4 ) . Тогда объем параллелепипеда, построенного на векторах

AB ,

AC и AD как на сторонах, вычисляется по формуле

1

1

1

1

V = mod

x1

x2

x3

x4

.

(2.35)

y

y

y

y

1

2

3

4

z1 z2 z3 z4

Доказательство. Преобразуем правую часть (2.35), используя свой-

ства определителей:

1

1

1

1

1

0

0

0

x2

- x1

x3 − x1

x4 − x1

x1

x2

x3

x4

x1

x2 - x1

x3 − x1

x4

− x1

mod

= mod

= mod

y

- y

y - y

y

− y

=

y1 y2 y3 y4

y1 y2 - y1 y3 - y1

y4

− y1

2

1

3

1

4

1

z2

- z1

z3 - z1

z4 − z1

z1 z2 z3 z4

z1

z2 - z1

z3 - z1

z4 − z1

= mod(AB AC AD) =V . Теорема доказана.

Следствие. Объем треугольной пирамиды с вершинами в точках A(x1, y1, z1) , B(x2 , y2 , z2 ) , C(x3, y3, z3 ) , D(x4 , y4 , z4 ) вычисляется по формуле

				1	1	1	1
	V =	1	mod	x1	x2	x3	x4	.	(2.36)
		6		y	y	y	y
				1	2	3	4
				z1	z2	z3	z4

Доказательство. Если четыре вершины параллелепипеда, не лежащие в одной плоскости, являются вершинами треугольной пирамиды, то

объем пирамиды составляет	1	объема параллелепипеда. Учитывая, что
	6

объем параллелепипеда вычисляется по формуле (2.35), получаем доказываемое тождество. Следствие доказано.

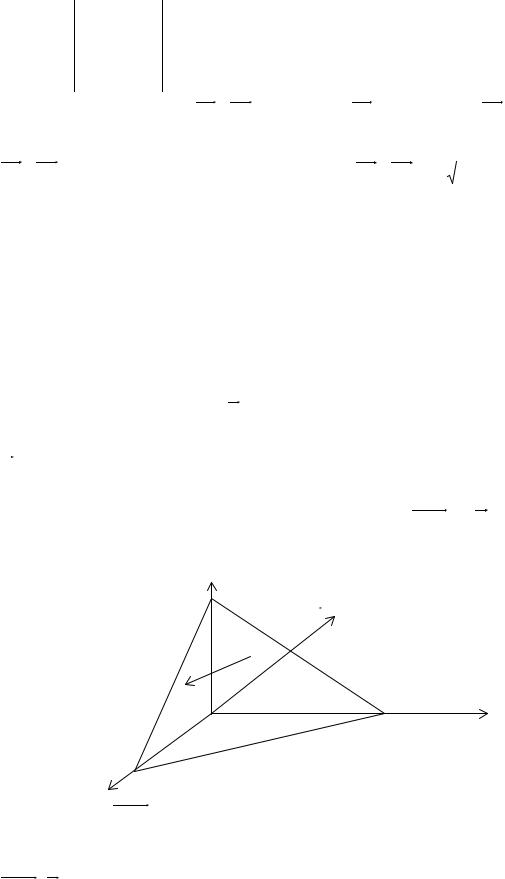
П р и м е р 29.	Вершины тетраэдра находятся в точках A(2, 3,1) ,
B (4,1, − 2) , C (6, 3, 7) и	D (−5, − 4, 8) . Найти длину высоты h тетраэдра, опу-

щенной из вершины D .

Решение. Так как объем V тетраэдра и его высота h связаны соот-

ношением V =	1 h S , где S − площадь грани ABC , то h =			3V . Объем V тет-
	3			S
раэдра и площадь S грани ABC найдем, используя векторное и смешанное
произведения	векторов.	По	формуле	(2.36)	имеем:
		58

1

1

1

1

V =	1 mod	2	4	6	−5		=	1		308 = 154			. Из определения векторного произведе-
	6	3	1	3	− 4			6	3
		1 − 2		7	8
ния	следует,			что S =				1		AB× AC		.	Так	как		AB = {2, − 2, −3}, AC = {4, 0, 6},					то
		i		j	k			2							1				= 1
						= {−12, − 24, 8}							и
AB× AC =		2	− 2		−3									S =			AB× AC			(−12) + (−24)2 +82	=
		4		0	6										2				2

=14. Таким образом, h =11.

3.АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ

3.1. Общее уравнение плоскости

Пусть в пространстве задана прямоугольная система координат Oxyz ,

точка M0 (x0 , y0 , z0 ) и вектор	N = {A, B,C}.	Выведем уравнение плоскости π ,
проходящей через точку	M0 (x0 , y0 , z0 )	и перпендикулярной вектору
N = {A, B,C}.

Пусть M(x, y, z) − произвольная точка плоскости π . Точка M лежит в

плоскости π тогда и только тогда, когда векторы M0M и N взаимно перпендикулярны.

	z
	N
	M0
M	y
	O
x

Вектор M0M имеет координаты {x − x0 , y − y0 , z − z0}. Необходимым и

достаточным условием перпендикулярности векторов является равенство нулю их скалярного произведения, т. е. должно выполняться равенство

M0M N = 0 . Воспользовавшись формулой (2.21), получим:

A(x − x0 ) + B(y − y0 ) +C(z − z0 ) = 0 .

(3.1)

59

Уравнение (3.1) − искомое уравнение плоскости π , проходящей через точку M0 (x0 , y0 , z0 ) и перпендикулярной вектору N = {A, B,C}, так как ему удовлетворяют координаты (x, y, z) любой точки M , лежащей на плоскости π , и не удовлетворяют координаты никакой точки, не лежащей на этой

плоскости.
Если	в уравнении (3.1) раскрыть скобки и	обозначить
D = −Ax0 − By0 −Cz0 , то получим общее уравнение плоскости:
	Ax + By +Cz + D = 0 .	(3.2)

Таким образом, плоскость является поверхностью первого порядка, так как определяется уравнением первой степени.

Теорема 1. Всякое уравнение первой степени вида (3.2) определяет в заданной системе координат плоскость.

Доказательство. Пусть заданы прямоугольная система координат Oxyz и уравнение Ax + By +Cz + D = 0 , коэффициенты которого удовлетво-

ряют условию A2 + B2 +C2 ≠ 0 , т. е. хотя бы один из коэффициентов A, B, C

отличен от нуля. Для определенности будем считать, что A ≠ 0 . Уравнение (3.2) имеет решение (x0 , y0 , z0 ) , так как при фиксированных y0 и z0 из урав-

нения (3.2) получим x0 = − BA y0 − CAz0 − DA . Следовательно, существует хотя

бы одна точка M0 (x0 , y0 , z0 ) , координаты которой удовлетворяют уравнению (3.2), т. е. Ax0 + By0 +Cz0 + D = 0 . Вычитая это числовое равенство из уравнения (3.2), получим уравнение A(x − x0 ) + B(y − y0 ) +C(z − z0 ) = 0 , эквивалентное данному Ax + By +Cz + D = 0 , поэтому уравнение Ax + By +Cz + D = 0 определяет плоскость, проходящую через точку M0 (x0 , y0 , z0 ) и перпендику-

лярную вектору N = {A, B,C}. Теорема доказана.
П р и м е р 30.	Составить общее уравнение плоскости, проходящей
через точку M0 (−1, 2,1)	перпендикулярно вектору N = {4, 2, - 5}.
Решение. С использованием (3.1) имеем: 4(x +1) + 2(y − 2) −5(z −1) = 0 ,
или 4x + 2y −5z +5 = 0 .
Определение. Вектор N = {A, B,C}, перпендикулярный плоскости π ,
задаваемой уравнением Ax + By +Cz + D = 0 , называется нормальным век-
тором этой плоскости.

	Теорема 2. Если два уравнения A1x + B1 y +C1z + D1 = 0 и A2 x + B2 y +C2 z +
+ D2	= 0	определяют одну и ту же плоскость, то найдется такое число t , что
справедливы равенства A1 = A2t ,				B1 = B2t , C1		= C2t , D1 = D2t , т.е. коэффициен-
ты уравнений пропорциональны.
	Доказательство.		Уравнения		A1x + B1 y +C1z + D1 = 0		и A2 x + B2 y +C2 z +
+ D2	= 0	определяют	одну и	ту	же	плоскость,	поэтому векторы

N1 = {A1, B1,C1} и N2 = {A2 , B2 ,C2} коллинеарны. Согласно условию (2.28) кол-

60

N1 = {A1, B1,C1} и

	линеарности имеем:	A1	=	B1	=	C1		= t , т. е.	A1 = A2t , B1 = B2t , C1 = C2t . Подста-
		A		B
						C	2
		2		2

вим выражения для коэффициентов A1, B1, C1 в первое уравнение плоскости,

получим: (A2 x + B2 y +C2 z)t + D1 = 0. Выражение, стоящее в скобках, равно − D2 , поэтому D1 = D2t. Теорема доказана.

3.2. Угол между плоскостями

Рассмотрим две плоскости π1 и π2 , которые задаются уравнениями

A1x + B1 y +C1z + D1 = 0 и A2 x + B2 y +C2 z + D2 = 0 .

При любом расположении плоскостей в пространстве один из углов

ϕмежду ними равен углу между их нормальными векторами N1 = {A1, B1,C1}

иN2 = {A2 , B2 ,C2} и вычисляется по формуле:

cosϕ =	N N			2			=							AA + B B +C C							2				.	(3.3)
	1													1 2				1 2		1
	N		N								2			2			2			2	2	+C	2
					2							A + B			+C				A + B				2
	1										1			1		1				2	2
Второй угол ϕ1	между плоскостями равен π −ϕ и cosϕ1																									= −cosϕ .
Две плоскости π1			и π2						параллельны тогда и только тогда, когда их
нормальные векторы N1			и N2						коллинеарны. В этом случае
									A1		=		B1	=	C1 .											(3.4)
								A					B
															C	2
									2		2

Условие (3.4) является условием параллельности двух плоскостей,

задаваемых уравнениями A1x + B1 y +C1z + D1 = 0 и A2 x + B2 y +C2 z + D2 = 0 .

Две плоскости π1 и π2 взаимно перпендикулярны тогда и только то-

гда, когда их нормальные векторы N2 = {A2 , B2 ,C2} ортогональны, т. е. косинус угла ϕ между ними равен нулю. Поэтому условие перпендикулярности плоскостей определяется соотношением

A1 A2 + B1B2 +C1C2 = 0 .

(3.5)

3.3. Неполные уравнения плоскости. Уравнение плоскости в отрезках

Определение. Общее уравнение (3.2) плоскости называется полным, если все его коэффициенты A, B, C, D отличны от нуля. Если хотя бы

один из указанных коэффициентов равен нулю, то уравнение называется

неполным.

Рассмотрим все возможные виды неполных уравнений.

1. D = 0 . Уравнение Ax + By +Cz = 0 определяет плоскость, проходящую через начало координат, так как координаты точки O (0, 0, 0) удовлетворяют этому уравнению.

61

Ax = 0

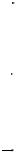
2.	A = 0 . Уравнение By +Cz + D = 0	определяет плоскость, параллель-
ную оси Ox , так как нормальный вектор			N = {0, B,C} этой плоскости пер-
пендикулярен оси Ox .
3.	B = 0 . Уравнение Ax +Cz + D = 0	определяет плоскость, параллель-
ную оси Oy , так как нормальный вектор			N = {A, 0,C} этой плоскости пер-
пендикулярен оси Oy .
4.	C = 0 . Уравнение Ax + By + D = 0	определяет плоскость, параллель-
ную оси Oz , так как нормальный вектор			N = {A, B, 0} этой плоскости пер-
пендикулярен оси Oz .
5.	A = 0, B = 0 . Уравнение Cz + D = 0		определяет плоскость, парал-
лельную координатной плоскости Oxy ,		так как эта плоскость параллельна
осям Ox и Oy .
6.	A = 0, C = 0. Уравнение By + D = 0		определяет плоскость, парал-

лельную координатной плоскости Oxz, так как эта плоскость параллельна осям Ox и Oz .

7. B = 0, C = 0. Уравнение Ax + D = 0 определяет плоскость, параллельную координатной плоскости Oyz, так как эта плоскость параллельна осям Oy и Oz .

8. A = 0, B = 0, D = 0 . Уравнение Cz = 0 определяет координатную плоскость Oxy , так как эта плоскость параллельна Oxy и проходит через

начало координат.

9. A = 0, С = 0, D = 0 . Уравнение By = 0 определяет координатную

плоскость Oxz, так как эта плоскость параллельна Oxz и проходит через начало координат.

10. B = 0, С = 0, D = 0 . Уравнение определяет координатную плоскость Oyz, так как эта плоскость параллельна Oyz и проходит через

начало координат.

Рассмотрим полное уравнение (3.2) плоскости. В этом уравнении все коэффициенты отличны от нуля, поэтому его можно переписать в виде

x

+

y

+

z

=1, или

−

D

−

D

−

D

A

B

C

x

y

z

+

+

=1,

(3.6)

= − D

= − D

c = − D

a

b

c

где a

,

b

,

− величины отрезков, отсекаемых плоскостью

A

B

C

на осях Ox , Oy и Oz соответственно. Уравнение (3.6) называется уравнением плоскости в отрезках.

3.4. Уравнение плоскости, проходящей через три различные точки, не лежащие на одной прямой

62

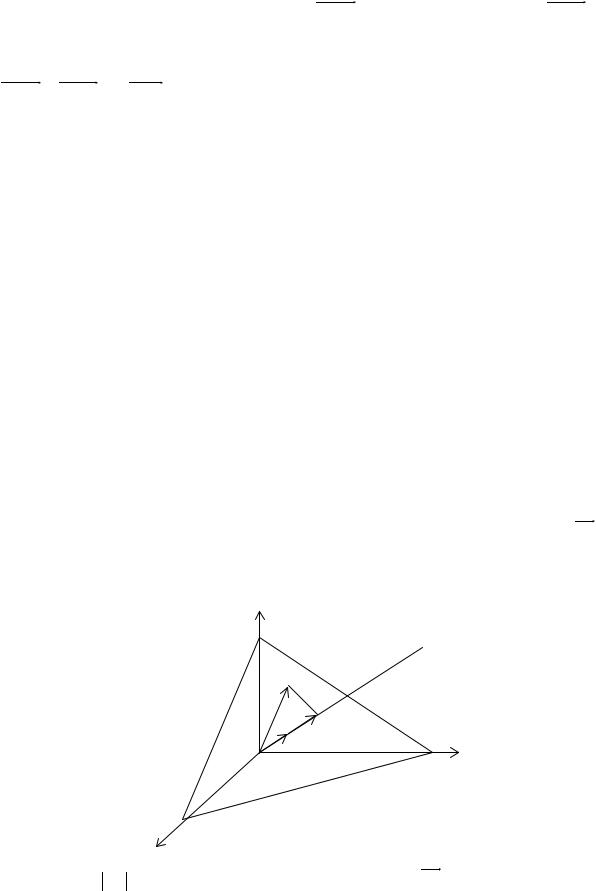
Пусть три точки M1(x1, y1, z1) , M2 (x2 , y2 , z2 ) и M3 (x3, y3, z3 ) не лежат на

одной прямой. В этом случае векторы М1M2 = {x2 − x1, y2 − y1, z2 − z1} и M1M3 = = {x3 − x1, y3 − y1, z3 − z1} не коллинеарны, поэтому точка M(x, y, z) лежит в одной плоскости с точками M1 , M2 и M3 тогда и только тогда, когда векторы

M1M2 , M1M2 и M1M компланарны, т. е. тогда и только тогда, когда сме-

шанное произведение этих трех векторов равно нулю. Используя выражение (2.34) смешанного произведения векторов в координатах, получим необходимое и достаточное условие принадлежности точки M(x, y, z) к плос-

кости, проходящей через точки M1 , M2 и M3 :

	x - x1	x2 − x1 x3 − x1			= 0.	(3.7)
	y - y1	y2 - y1	y3 − y1
	z - z1	z2 - z1	z3 − z1
Уравнение (3.7) первой степени и является уравнением искомой
плоскости, проходящей через три точки M1(x1, y1, z1) ,						M2 (x2 , y2 , z2 ) и
M3 (x3, y3, z3 ) , не лежащие на одной прямой.

3.5. Нормальное уравнение плоскости. Расстояние от точки до плоскости

Рассмотрим произвольную плоскость π . Проведем через начало координат O прямую n , перпендикулярную плоскости π , которую будем называть нормалью. Точка P − пересечение плоскости и нормали. Введем направление от точки O к точке P , т. е. на прямой n возьмем единичный

вектор n , направление которого совпадает с направлением отрезка OP . Если точки O и P , совпадают, то направление вектора n выберем произвольно.

z
M
n	P	y
O

π

x

Пусть OP = p , α, β, γ − углы, которые вектор OP составляет с осями Ox , Oy и Oz соответственно. Тогда координатами вектора n будут направ-

63