1.3. Унитарные пространства. Скалярное произведение и ортогональность

В обычном трехмерном векторном пространстве, описанном выше, для каждых двух векторов скалярное произведение вводится как:

.

Для каждого вектора естественно вводится его длина (норма): и угол между векторами. Это пространство известно еще со времен Евклида (IV век до н. э.) и называется евклидовым.

Унитарное пространство – это такое линейное пространство E, в котором скалярное произведение вводится с помощью следующих аксиом:

1) ; число (знак * означает комплексное сопряжение).

2) ;

3) ;;a – комплексное число;

4) .

Унитарное пространство является нормированным с нормой . Для его элементов выполняетсяНеравенство Шварца:

.

Унитарное пространство является обобщением евклидова пространства.

Приведем примеры унитарных пространств.

1. Многомерное векторное пространство со скалярным произведением

; .

2. Пространство функций (в общем случае комплексных) L₂[a,b] со скалярным произведением

причем .

Одним из удивительных свойств унитарного пространства является наличие в нем ненулевых ортогональных элементов, для которых скалярное произведение равно нулю: .

Как известно, в трехмерном векторном пространстве ортогональные вектора составляют между собой угол 90^о. В частности, ортогональными называются две функции f(x) и g(x) из L₂, если (f, g)=0.

Ортогональной системой называется счетное множество (конечное или бесконечное) элементов {₁,…,_j,…}  Е, если все они попарно ортогональны:

.

Ортонормальной системой называется ортогональная система из элементов {e₁,…,e_j,…}, имеющих единичную норму: .

Легко заметить, что нормированные элементы получаются из ненормированных по формуле: .

Любое конечное число различных элементов ортогональной системы линейно независимо. Поэтому в унитарном пространстве ортогональные системы, как правило, выбирают в качестве системы базисных функций (базиса).

В полном унитарном пространстве любая функция может быть представлена в виде линейной комбинации элементов базиса (не обязательно ортогонального).

Для любого элемента u унитарного пространства E число a_k=(u,e_k)= называется коэффициентом Фурье элемента u относительно ортонормальной системы {…e_k…}={…,,…}, а ряд:

– обобщенным рядом Фурье для элемента u. При этом выполняется равенство Бесселя: , которое являетсяусловием полноты системы базисных функций.

Имеет место теорема о том, что отрезок ряда Фурье являетсянаилучшей аппроксимацией элемента u в унитарном пространстве. То есть если искать коэффициенты a_k из условия , то они получаются какa_k=(u,e_k).

Примеры систем ортогональных базисных функций.

1. В пространстве L₂[–1,1] кусочно-непрерывных функций c точками разрыва первого рода ортонормальным является базис:

{1/, cos x, sin x, cos 2x, sin 2x,… cos kx, sin kx,…}.

Свойства ортонормальности базиса:

,

,

.

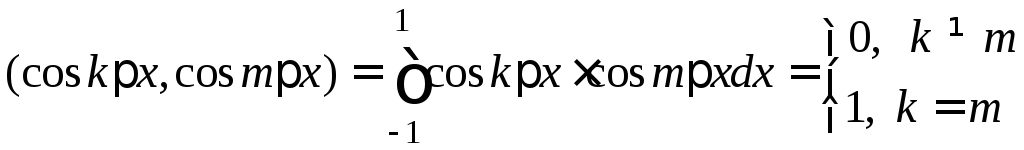Разложение функции f  L₂[–1,1] в ряд Фурье по этому базису:

.

Коэффициенты Фурье:

, ,,k = 1,2,…

2. Базис из ортогональных многочленов Лежандра, x  [–1,1]:

{L₀(x), L₁(x), L₂(x), L₃(x), L₄(x),…, L_k(x),…}=

={L₀ = 1, L₁ = x, L₂ = (3x² - 1)/2, L₃ = (5x³ - 3x)/2, L₄ = (35x⁴ - 30x²+3)/8,…}.

Формула Родрига: .

.

Обобщенный ряд Фурье: .

Обобщенные коэффициенты Фурье: .