И.И. ЛОБУНИНА

ОСНОВЫ ЛИНЕЙНОЙ АЛГЕБРЫ

УЧЕБНОЕ ПОСОБИЕ

САНКТ -ПЕТЕРБУРГ

2006

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение

высшего профессионального образования

СЕВЕРО-ЗАПАДНЫЙ ГОСУДАРСТВЕННЫЙ ЗАОЧНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

И.И. ЛОБУНИНА

ОСНОВЫ ЛИНЕЙНОЙ АЛГЕБРЫ

Утверждено редакционно-издательским советом университета в качестве учебного пособия

Санкт-Петербург

2006

УДК 517 (07)

Лобунина И.И. Основы линейной алгебры: Учебное пособие.

СПб.: СЗТУ, 2006, - 76 с.

Пособие содержит теоретический материал, иллюстрируемый большим количеством подробно разобранных примеров, по трем разделам линейной алгебры: определители, системы линейных уравнений и матрицы. Пособие предназначено для студентов всех специальностей. Содержание пособия отвечает требованиям Государственных образовательных стандартов высшего профессионального образования.

Научный редактор А.А.Потапенко, доктор физ.-мат. наук, проф.

Рецензенты: кафедра вычислительной математики СевероЗападного государственного заочного технического университета (заведующий кафедрой Г.Г.Ткаченко, канд.физ.-мат.наук, доцент); В.М.Фролов, канд.физ.-мат.наук, доцент кафедры высшей математики Санкт-петербургского государственного института точной механики и оптики (технического университета).

©Северо-Западный государственный заочный технический университет 2006

©Лобунина И.И.,2006

Глава 1 ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

Мы начинаем изучение курса математики с линейной алгебры, одной из задач которой является исследование и решение произвольных систем алгебраических уравнений первой степени – систем линейных уравнений. К подобным системам приводит большое число практических задач (в частности, задач оптимизации), решаемых в различных областях науки, техники, экономики и маркетинга..

Поиск наиболее эффективных методов решения систем линейных уравнений привел к развитию специального математического аппарата

– теории определителей и матриц, овладение которой и является целью первого раздела курса математики.

1.1 Общая запись системы линейных уравнений. Основные определения

В теории систем линейных уравнений для удобства записи и исследования принимается следующая система обозначений: неизвестные будем обозначать буквой x с соответствующими индексами: x1, x2 ,..., xn ; уравнения будем считать перенумерованными; коэффици-

енты при неизвестных обозначаются одной буквой aik с двумя индексами i и k , где i - номер уравнения, k - номер неизвестного. Эти индексы следует читать раздельно, например, коэффициент a21 читается

“ a два один”, а не “ a двадцать один”. Свободные члены обозначим через bi , где i - номер уравнения. Тогда в самом общем случае система из

m линейных уравнений с n неизвестными записывается в виде

a11x1 +a12 x2						+... +a1n xn =b1,
		+a22 x2				+... +a2n xn				=b2 ,
a21x1											(1.1)
			................
a	x	+a	m2	x	2	+... +a	mn	x	n	=b .
	m1 1									m

Коэффициенты при неизвестных составляют прямоугольную таблицу из m строк и n столбцов, называемую матрицей системы* (1.1), обозначаемой

3

		a11	a12	...	a1n
A =		a21	a22	...	a2n		(1.2)
		...	... ... ...
		am1	am2	...	amn

* Определение понятия матрицы будет дано в главе 2.

Матрицы как особые таблицы обозначаются сдвоенными вертикальными черточками, круглыми или квадратными скобками.

Решением системы линейных уравнений (1.1) называется такая совокупность n чисел C1,C2 ,...,Cn , что при замене неизвестных x1 на

С1, x2 на C2 ,..., xn на Cn каждое из уравнений системы обращается в тождество. (Подчеркнем, что C1,C2 ,...,Cn , составляют одно решение

системы, а не n решений).

Система линейных уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.

Так, например, система

x1 +3x2 =1x1 +3x2 = 7

несовместна, так как левые части уравнений совпадают, но правые различны. Никакая совокупность значений неизвестных не может удовлетворить обоим уравнениям, так как заданные уравнения противоречат друг другу.

Совместная система называется определенной, если она имеет только одно решение и неопределенной, если решений больше чем одно.

Как будет показано далее, неопределенная система имеет бесчисленное множестворешений.

Например, система

2x1 − x2 =1x1 + x2 =5

определенна, так как имеет единственное решение x1 = 2, x2 =3. Рассмотрим систему

4

5x1 − x2 = 2 ,10x1 −2x2 = 4

в которой коэффициенты при неизвестных и свободные члены пропорциональны. Мы имеем на самом деле одно уравнение с двумя неизвестными, допускающее бесконечное множество решений. То есть исходная система неопределенна, так как имеет бесчисленное множество решений вида

x1 =t; x2 =5t −2,

где t - любое число.

Две системы называются эквивалентными (равносильными),если каждоерешение первойсистемыявляетсярешением второй,и наоборот.

Задача теории систем линейных уравнений заключается в разра-

ботке методов, позволяющих определить, совместна ли данная система уравнений или нет, и в случае совместности установить число решений, а также указать способ нахождения всех этих решений.

Применение определителей и матриц в теории линейных систем позволяет разработать методы исследования этих систем и способы их решения. Общий случай системы (1.1) будет рассмотрен во второй главе, а главное внимание мы уделим системам, в которых число уравнений равно числу неизвестных, начиная с простейших случаев n = 2 и n =3.

1.2 Система двух линейных уравнений с двумя неизвестными. Определитель второго порядка

Изучение теории определителей начнем с рассмотрения простейшего случая системы двух линейных уравнений с двумя неизвестными. Запишем эту систему в общих обозначениях, принятых в 1.1.

a		x +a		x	=b	(1.3)
	11	1	12	2	1
a21x1 +a22 x2					=b2

Будем решать эту систему знакомым из элементарной алгебры методом исключения неизвестных, чтобы получить новую систему, эквивалентную данной, где каждое уравнение содержит только одно неизвестное. Для исключения неизвестного x2 умножим обе части первого уравнения

на a22 , а второго - на —a12 и сложим почленно полученные равенства. Для исключения x1 возьмем в качестве множителей числа: —a21- для первогоуравнения и a11 - для второго.

5

В результате получим

	(a11a22 −a12a21)x1 =b1a22	−a12b2	,	(1.4)
	(a11a22 −a12a21)x2 = a11b2 −b1a21.

Вуравнениях (1.4) коэффициентом при неизвестных является одно

ито же число

a11a22 −a12a21,

(1.5)

получаемое по определенному правилу из элементов матрицы. систе-

мы A:

A =		a11	a12		.	(1.6)
		a	a
		21	22

Матрица, имеющая две строки и два столбца, называется квад-

ратной матрицей второго порядка (матрицей второго порядка). Чис-

ла, составляющие матрицу, называются элементами матрицы.

В главе 2 теория матриц будет рассмотрена подробнее. Строки матрицы нумеруются сверху вниз, а столбцы - слева направо. Каждый элемент матрицы aik имеет два индекса: первый индекс i указывает но-

мер строки, а второй - k - номер столбца, на пересечении которых находится данный элемент. У квадратной матрицы любого порядка совокупность элементов a11, a22 ,..., ann , расположенных на диагонали, идущей из

левого верхнего угла матрицы в правый нижний, называется главной диагональю, а совокупность элементов, расположенных на второй диагонали, называется побочной диагональю матрицы.

Важнейшей числовой характеристикой квадратной матрицы является ее определитель - число, получаемое по определенному правилу по элементам матрицы. (Идея введения определителей принадлежит выдающемуся немецкому математику ГотфридуЛейбницу1646-1716).

Определение. Определителем матрицы второго порядка (1.6) (определителем второго порядка) называется число, равное разности произведений элементов главной и побочной диагоналей, обозначаемое символом

a11 a12 . a21 a22

Таким образом, поопределению,

6

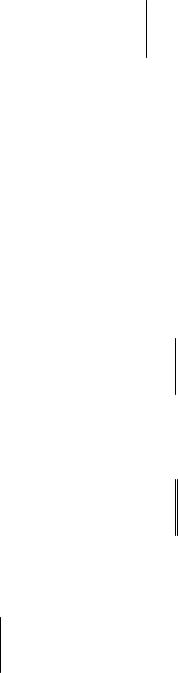
a11	a12	= a a	22	−a a	21	.	(1.7)
a21	a22	11		12

Подчеркнем еще раз принципиальное различие между матрицей и ее определителем. Матрица - таблица чисел; определитель квадрат-

ной матрицы - число, получаемое по определенному правилу из элементов матрицы. Определитель в отличие от матрицы обозначается простыми, а не сдвоеными вертикальными черточками. Определитель (1.7) матрицы системы (1.6) называется определителем системы (1.3). Таким образом, коэффициентом при неизвестных x1 и x2 в системе (1.4) яв-

ляетсяопределитель исходной системы (1.3). Свободные члены, стоящие в правых частях уравнений системы (1.4), также являются определителями второго порядка. Свободный член в первом уравнении является определителем матрицы

	b1	a12				,	(1.8)
	b2	a22

получающейся из матрицы системы (1,6) заменой первого столбца столбцом из свободных членов b1 и b2 а свободный член во втором урав-

нении - определитель матрицы

a11		b1		,	(1.9)
a	21	b
		2

получающейся из той же матрицы системы (1.6) заменой второго столбца столбцом изсвободныхчленов.

Если ввести обозначения

a11

a12

=D;

b1

a12

= D ;

a11

b1

= D ,

(1.10)

a

21

a

22

b

a

22

1

a

21

b

2

2

2

то система уравнений (1.4) запишется в виде

Dx		= D	(1.11)
	1	1 ,
Dx2		= D2

Исследуем систему (1.11). Возможны два случая: либо определитель D системы отличен от нуля, либо равен нулю.

I. D ≠0.

Если определитель D системы (1.3) отличен от нуля, то система (1.11) имеет только одно решение:

7

x =	D1	;	x =	D2	.	(1.12)
1	D		2	D
Покажем, что в случае D≠0 решение (1.12) является также реше-
нием исходной системы (1.3). Подставив значения						x1 и x2 , получаемые

по формулам (1.12), в уравнения системы (1.3), убеждаемся, что они удовлетворяют уравнениям этой системы:

a				D1			+a		D2					=	1					[a (b a										22		−a b ) +a (a b −b a					)] =
										D					D
11 D							12																11			1						12 2	12		11 2	1 21
=		1			b (a a						−a a							21				) =				1			b D =b
																										D
		D 1					11 22							12																1		1
a				D1			+a			D2				=			1				[a				(b a							−a b ) +a			(a b −b a			)] =
	21 D							22		D							D							21							22			22
																										1						12 2			12 2	1 21
=		1			b (a a						−a a									21			) =			1			b D =b .
																											D
		D 2					11 22							12																	2	2
Можно показать,														что в рассматриваемом случае																						D≠0 система

(1.3) других решений не имеет, то есть решение (1.12) является единственным, а системы (1.11) и (1.3) эквивалентными.

Полученный результат является частным случаем теоремы Крамера применительно к системе двух линейных уравнений с двумя неизвестными. Общий случай теоремы Крамера приведен в 1.6. (Габриэль Крамер (1704-1752) - швейцарский математик).

Теорема Крамера. Если определитель системы двух линейных уравнений с двумя неизвестными отличен от нуля, то система совместна и имеет единственное решение. В этом решении каждое неизвестное равно дроби, знаменатель которой равен определителю системы, а числитель - определителю матрицы, получающейся из матрицы системы заменой столбца коэффициентов при вычисляемом неизвестном столбцом из свободныхчленовсистемы.

Формулы (1.12) называются формулами Крамера для системы двух линейных уравнений с двумя неизвестными.

II. D=0.

Если определитель системы (1.3) равен нулю, то система либо несовместна (не имеет решений), либо неопределенна (имеет бесконечное

8

множество решений). Это зависит от определителей D1и D2 . При этом

возможны два исхода:

1)Если хотя бы один из определителей D1 или D2 отличенот нуля,

то по крайней мере одно из равенств (1.11) невозможно, то есть система (1.11) несовместна, а следовательно, и система (1.3) несовместна.

2)Если оба определителя D1и D2 .равны нулю, то система (1.11), а

следовательно, и система (1.3) неопределенна и эквивалентна одному из ееуравнений и, следовательно, имеетбесконечное множество решений.

Доказательства этих утверждений выходят за рамки нашей программы и могут быть найдены в более полных курсах линейной алгебры.

Пример 1. Решить систему

3x		−2x	2	=12	.	(1.13)
	1
	5x1 + x2 = 7

Решение. Вычислим определитель системы

D = 53 −21 =3 1−(−2) 5 =13.

Так как D ≠ 0, то система имеет единственное решение (система определенна). Это решение находим по формулам Крамера (1.12). Вычислим определители D1 и D2 :

	D	=			12			−2						=12 1−(−2) 7 = 26;
	1				7			1
	D 2 =						3	12			=				3 7 −12 5 = −39.
							5	7
Определимнеизвестные:
	x =			D1				=	26					= 2; x =				D2	= −	39	= −3.
	1				D			13									2	D	13
Проверка. Подставим x1 = 2 и x2 = −3 в уравнения системы.
3 2 −2 (−3) =12			, система решена правильно.
	= 7
5 2 +(−3)
Пример 2. Решить систему
							x +2x									= 6	.		(1.14)
								1							2
							3x1 +6x2 = 4

9

Решение. Вычислим определитель системы

D = 13 62 = 6 −6 = 0.

Так как D = 0 , то данная система либо несовместна, либо неопределенна. Найдем D1 и D2

D =		6			2			=36 −8 = 28;
1		4			6
D =				1	6			= 4 −18 = −14.
2				3	4

Так как определитель системы D = 0, а определители D1 и D2

отличны от нуля, то сиcтема несовместна. Это же можно установить, умножив обе части первого уравнения системы на 3. Получим уравнение 3x1 +6x2 =18, которое противоречит второму уравнениюсистемы.

Пример 3. Решить систему

	x	−3x	2	= 2	.	(1.15)
	1
−2x1 +6x2 = −4

Решение. Вычислим определители D, D1, D2

1 −3

D =

= 6 −6 = 0;

−2

6

D

=

2

−3

=12 −12 = 0;

1

−4

6

D

=

1

2

= −4 −(−4) = 0.

2

−2

−4

Так как все определители равны нулю, то система неопределенна (имеет бесконечное множество решений). В этом случае она эквивалентна одному уравнению, например, первому. (Легко заметить, что второе уравнение является следствием первого - оно получается умножением всех членов первого уравнения на -2). Поэтому всякое решение первого уравнения является и решением системы. Придавая x2 любые числовые

значения, находим соответствующие значения для x1 по формуле

10

x1 = 2 +3x2.. Таким образом, множество всех решений системы можно

записать ввиде:

x1 = 2 +3x2 , где x2 R.

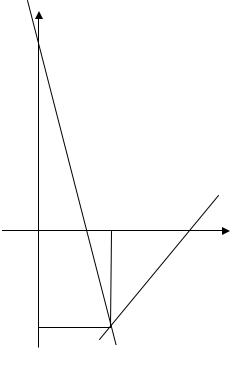
Рассмотренный в этом параграфе случай системы двух линейных уравнений с двумя неизвестными имеет простую геометрическую интерпретацию. Воспользуемся графическим изображением линейных уравнений системы (1.3) в прямоугольной декартовой системе координат Oxy,

считая, что x1 = x, x2 = y . Из школьного курса математики известно, что

каждому линейному уравнению рассматриваемой системы соответствует на координатной плоскости определенная прямая. Построив прямые, определяемые уравнениями, входящими в системы примеров 1,2,3, мы получим наглядные изображения, иллюстрирующие особенности этих систем.

Запишем систему (1.13) в виде

		y		3x −2 y =12,
				5x + y = 7.
				На рисунке 1.1 изображены прямые, со-
		5x + y = 7		ответствующие уравнениям этой системы.
				Напомним, что для построения прямой дос-
				таточно определить координаты двух то-
			3x −2 y =12	чек, принадлежащих этой прямой, напри-
				мер, точек ее пересечения с осями коорди-
	O	2		нат. Для этого нужно в уравнении прямой
			4	принять y = 0, получим координату x точ-
				ки пересечения этой прямой с осью Ox;
				приняв x = 0, получим координату y точки
	−3		M1(2,−3)	пересечения данной прямой с осью Oy .
		Рис.1.1.		Построив таким образом прямые
				3x −2 y =12 и 5x + y = 7 , найдем точку пе-

ресечения M1(2;−3) этих прямых, соответствующую единственному ре-

шению системы (1.13). Запишем систему (1.14) в виде

x +2 y = 6,3x +6 y = 4.

11