3.Вогнутость.
Кривая называется вогнутой (выпуклой) кверху на отрезке ab, если она лежит ниже любой касательной в любой точке отрезка ab.
Теорема 1(необх. усл. выпуклости(вогнутости)).
Пусть y= f(x) непрерывна и дважды дифференцируема:
если y= f(x) вогнута кверху => f ́ ́(x)≤0,
если y= f(x) вогнута книзу => f ́ ́(x) ≥0.
Иллюстрация-док.
x<x=>α<α=>tg α<tgα=>f ́(x)< f ́(x)
=>f ́(x)↑=> f ́ ́(x)≥0
=> f ́(x)↓=> f ́ ́(x)≤0
Теорема 2 (дост. усл. выпуклости(вогнутости)).
y= f(x) непрерывна и дважды дифференцируема,
f ́(x)>0=>y= f(x) вогнута книзу
f ́(x)<0=>y= f(x) вогнута кверху
Док.
y= f(x) – кривая
Y>y справа
Y>y слева
y
0 0
Y-y>0-?
Y
0 0 0 0 0 0 0 0 1
4.Перегибы.
Опред. х- точка перегиба кривой y= f(x), если с одной стороны от этой
точки прямая вогнута кверху, а с другой стороны – книзу.
Теорема 1(необх. усл. перегиба)
y
0
х
0 0
Док.
Точка перегиба – точка экстремума для производной. В критической точке 2-го порядка нужно искать экстремумы.
Теорема 2(дост. усл. перегиба)
y
0
f ́(x) непрерывна в U(x )
f ́ ́(x) непрерывна в
Е
0
5.Ассимптоты.
1) Вертикальные
х=а называется асcимптотой (верт.) y= f(x), если lim f(x)=∞
x→a±0
2) Наклонные
y=kx+b называется асcимптотой (накл.) y= f(x), если lim (f(x)-(kx+b))=0
x→∞
y=g(x) называется асcимптотической кривой для y= f(x), если lim(f(x)-g(x))=0
x→±∞
Вывод уравнения накл. ассимптот:
lim (f(x)-kx-b))=0 (1)
x→∞
lim х(f(x)/х-k-b/х))=0
x→∞
lim (f(x)/х)=k =>подставляем в (1)
x→∞
lim (f(x)-kx)=b
x→∞
Исследование функции
1.Область определения, точки разрыва.
2. Множества значений.
3. Точки пересечения с осями.
4. Чётность, периодичность.
5. Монотонность, экстремумы.
6. Вогнутость, перегибы.
7. Асимптоты.
8. График.
Неопределённый интеграл.
Первообразная.
;
– первообразная
Теорема (о первообразных)
- первообразнаяf(x)
- первообразнаяf(x)
Док-во
;
Теорема Лагранжа
Неопределённый интеграл – это класс первообразных для функции f(x).
– подынтегральная функция;
–
подынтегральное выражение.
Свойства неопределённых интегралов.
1.
2.
3.
4.
Док-во
Теорема
Если функция не прерывна то она имеет первообразную.
- непр.
- непр., диф-ма.
- непр.
тогда
Док-во
Интегралы группы четырёх.
1)
2)
3) Интегрирование табличных интегралов.
1)-3) -||-||-||-
Интегрирование по частям.
Интегрирование рациональных функций.
- прав., если
- не прав., если
Простейшие дроби:
1.
2.
3.
4.
1.
2.
3. см. интеграл группы четырёх.
4. см интегрирование по частям.
Теорема1
- прав. дробь.
Док-во
,при этом
Следствие
Теорема2
- прав. дробь
Следствие
Интегрирование тригонометрических выражений.
Универсальная тригонометрическая
подстановка 
Пример 1.
Пример 2.
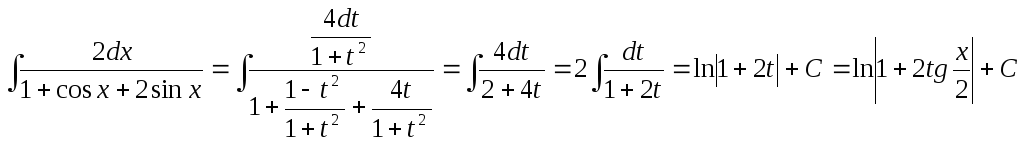
Частные случаи
,
гдеm+n–
четное,отриц.
,
гдеn– нечет.,nЄN
,
гдеm– нечет.,mЄN
,
гдеm,n-четные
Пример 3.
Пример 4.
Пример 5.
Пример 6.
Пример 7.
Интегрирование иррациональных выражений.
k – общий знаменатель
k – общий знаменатель
Пример 1.
Пример 2.
Интегрирование рациональных функций.
Выделение полного квадрата
Тригонометрические замены
Интегрирующий множитель.
(1)P(x,y)dx + Q(x,y)dy = 0
µ(x,y)
– интегрирующий множитель
(µ,P)dx+ (µ,Q)dy
Частные случаи интегрирующего множителя
1) µ=µ(x) µ
=0
2) µ=µ(y)
=0
Пример 1.
Уравнения высших порядков.
Поиск решения (1)удовлетворяющий условию (2) называется задачей Коши.
Теорема: (о существовании и единственности решения задачи Коши)
непрерывно вD
существует единственное решение
уравнение (1) удовлетворяет (2)
(*)
- общее решение уравнения (1), если
выполнено условие:
1) (*) – решение для любого
2)
(2)
)
– частное решение
- общий инт.
- частный инт.
(1)
(2)
Интеграл с переменным верхним пределом.
f(x)
интегрируем на [a,b]
=> интегрируем на [a,x]
x
∫f(t)dt=Φ(x), xЄ[a,b] интеграл с переменным верхним пределом
a
f(x) непр на [a,b] => Φ(x) непр на [a,b]
Φ´(x)=f(x)
Производная от интеграла с переменным верхним пределом = подинтегральной функции (т.е. первообразной)
Доказательство:
Формула Ньютона-Лейбница
x
∫f(t)dt – первообразная f(x), F(x) – любая первообразная f(x)
a
|
x ∫f(t)dt = F(x) +C a
|
подставляем вместо x,a
a
∫f(x)dt=f(a)+C
a
0= f(a)+C
C= - f(a)
x
∫f(t)dt = F(x) – F(a) x=b
a
b
∫f(t)dt = F(b) – F(a)
a
b
b
∫f(x)dx = F(x) = F(b) – F(a)
aa
Замена переменной в определенном интеграле
Теорема:
y=f(x) непр на [a,b]
x=φ(t) непр на [α,β]
φ(t): [α,β] → [a,b], a= φ(α), b= φ(β),=>
b β
∫f(x)dx =∫f(φ(t)) φ´(t)dt
a α
Док – во:
∫f(x)dx =∫f(φ(t)) φ´(t)dt
если F(x) – первообр. дляf(x), то
F(φ(t)) – первообр. для f(φ(t)) φ´(t)
b
∫f(x)dx = F(b) – F(a)
a
β
∫f(φ(t)) φ´(t)dt = F(φ(β)) – F(φ(α)) = F(b) – F(a)
α
например:
3
π/2
π/2
π/2
π/2
∫
√9-x2
dx=∫√9-9sin
2t
3cost dt=9∫cos2t
dt= 9/2∫(1+cos2t)dt=9/2(t+(sin2t)/2)
=9π/4
0 0 0 0 0
з
амена
x=3sint y=√9-x2
dx=3costdt y2=9-x2
x=0→t=0 x2+ y2=9
x=3→t= π/2
Интегрирование по частям в опред интеграле.
Теорема
u(x),v(x) непр,дифф-ма на [a,b] =>
b
b
b
∫udv = uv – ∫vdu
a a a
Док – во:
d(uv)=udv +vdu
b b b
∫d(uv) = ∫udv+∫vdu
a a a
b
b b
uv =∫udv+∫vdu,
a a a
b
b 
b
∫udv = uv – ∫vdu
a a a
например
π/2
π/2
π/2
π/2
π/2
∫xcosx dx=∫ xdsinx=xsinx – ∫sinxdx=π/2+cosx = π/2 – 1
0 0 0 0 0
дополнительные св-ва интегрела
e e
f(x) – чет =>∫ f(x)dx=2∫ f(x)dx
-e 0
Док-во:
e 0 e 0 e e e e
∫ f(x)dx=∫f(x)dx+∫ f(x)dx=∫f(–t)( –dt)+ ∫ f(x)dx=∫ f(t)dt+∫ f(x)dx=2∫ f(x)dx
-e -e 0 e 0 0 0 0
x
=
–t x= –e→t=e
dx=dt x=0 →t=0
e
f(x) – нечет =>∫ f(x)dx=0
-e
Док – во:
e 0 e 0 e e e
∫ f(x)dx=∫f(x)dx+∫ f(x)dx= –∫f(–t)( –dt)+ ∫ f(x)dx= – ∫ f(t)dt+∫ f(x)dx=0
-e -e 0 e 0 0 0
x
=
–t x=e→t=e
dx=dt x=0 →t=0
T a+T
f(x) –T-периодическая =>∫ f(x)dx=∫ f(x)dx a
0 a
(f(x+T)=f(X))
Док – во:
a+T 0 T a+T 0 T a
∫ f(x)dx=∫ f(x)dx + ∫f(x)dx+∫ f(x)dx=∫ f(x)dx+ ∫f(x)dx+ ∫f(t+T)dt=
a a 0 T a 0 0
a T a T
= – ∫f(x)dx+∫f(x)dx+∫ f(t)dt=∫f(x)dx
0 0 0 0
x
=
t+T x=T→t=0
dx=dt x=a+T →t=a
например:
2π π
∫(sin5 xcos34x+cos63x sinx+cosx)dx=∫(sin5 cos34x+cos63x sinx+cosx)dx=
0 нечетная нечетная четн 0
π
π
2∫cosxdx=2sinx=0
0