Некоторые применения.

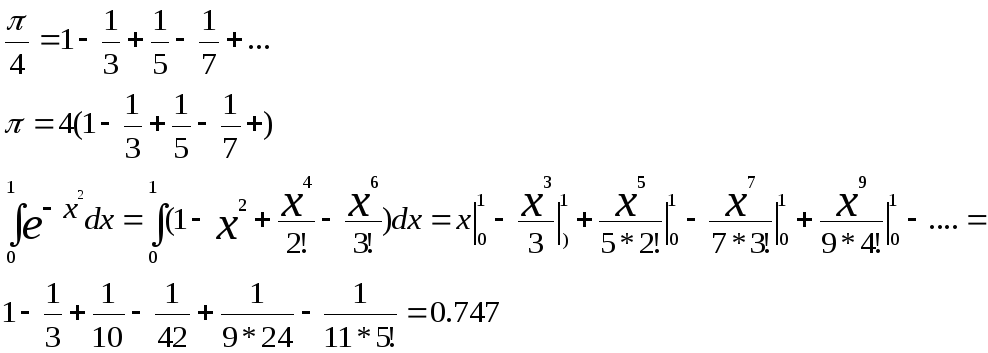
y(x)- ?

y(0)=y0

Пример.

Тригонометрический ряд

будем считать, что ряд сходится

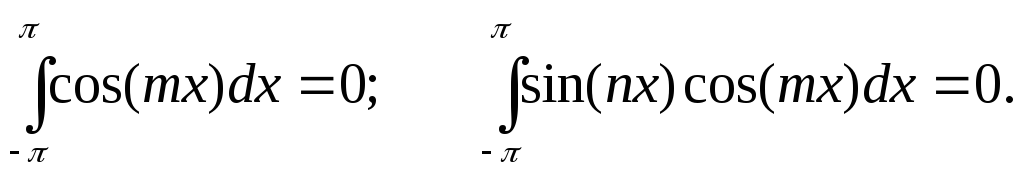
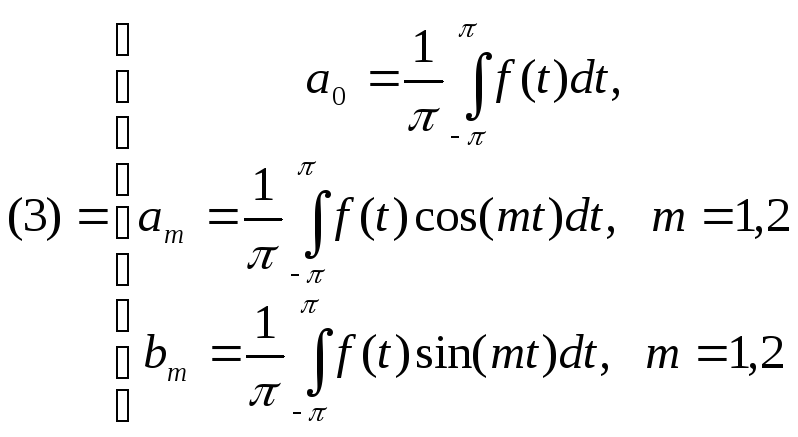
Коэффициенты Фурье функции f(x)

Теорема: Пусть – f(x) ограниченная, кусочно-непрерывная 2π – периодическая функция, сл-но f(x) можно представить рядом Фурье, причем если х₀ – точка непрерывности, то S(x₀)=f(x₀), если х₀ – точка разрыва,

имеем точку разрыва любого рода, причем конечное число на любом виде отрезков.

График

f(x) – четная

f(x) – нечетная

a₀=0, a_n=0

f(x) – 2l периодическая

Теорема: f(x) – ограниченная, кусочно-непрерывная, 2l – периодичная, следовательно, f(x) можно представить рядом Фурье (1), причем, если

Частные случаи:

Ряд Фурье. Разложение в ряд Фурье непериодической функции.

График

Частные случаи.

1. a=0 или b=0

График

0 – точка разрыва для (0,1,2,….) для а)

Интеграл Фурье.

f(x) – ограничена, кусочно-непрерывна, абсолютно интегрируется на (-∞, +∞), т.е. сходится

График.

Теория функций комплексного переменного:

Z=(x,y)

График

Z=x+iy (1) вектор разложений по базису (алгебраическая форма)

x=Re Z – действительная часть; y=Im Z – мнимая часть.

Если действительная часть = 0, то число чисто мнимое.

Если мнимая часть = 0, то число действительное.

Действия над комплексными числами

Сложение и вычитание

График

Умножение

Деление

Возведение в степень

Извлечение корня

Примеры:

График

Последовательности комплексных чисел.

График

Числовые ряды комплексных чисел.

∞

∑

n

z (1)

n=1

∞ ∞ ∞

1. ∑

   n

   n

   n

   n

   ( x +iy )=∑ x +i∑ y

n=1 n=1 n=1

∞

1. с

   n

   ходится  ∑ x - сходится

n=1

n

∞

∑ y - сходится

n=1

Степенные ряды комплексных чисел.

n

∞

(1) ∑ a zⁿ

n=0

Теорема Абеля.

0

Пусть (1) сходится при z=z => (1) сходится абсолютно при любом z:

0

׀ z׀<׀z ׀.

1

1

Пусть (1) расходится или сходится неабсолютно при z=z => (1) расходится при любом z: ׀ z׀<׀z ׀.

Доказательство как раньше (в теореме Абеля для некомплексных чисел вместо ׀х׀ используем ׀z ׀).

Следствие.

Ряд (1) сходится абсолютно при ׀ z׀>R, где R – радиус сходимости.

n

n+1

R=lim ׀a /a ׀

∞

(

n

1 ́) ∑ a (z-a) ⁿ

n=1

z

1 + z + z²/2! + z³/3! +…+ zⁿ/n! +…=e(2) –сходится абсолютно при любом z

z=x (ЄR)

x

e =1+x+x²/2+… - сходится ( - ∞; ∞)

x [1] + x[2]

x[1]

x[2]

a =a ∙a (x и z с индексами 1 и 2)

z [1] + z[2]

z[2]

z[1]

e =e ∙e

z[1]

e

1

1

1

=1+z +z²/2 +z³/6+…

z [1] + z[2]

e

2

1

2

1

= 1(z +z )+(z+z)²/2+…

z [1]

z [2]

e

1

2

2

1

1

2

1

2

1

1

2

2

1

2

1

2

1

2

1

1

1

2

2

2

2

2

2

1

1

1

∙e =1∙1+(1∙z +1∙z )+(z² /2+z² /2+z ∙z )+(z³ /6 +z³ /6 +z ∙z² /2 +z∙z²/2) +…=1+z +z +(z²+z² +2z z )/2+(z³+z³+3z z²+3z²z)/6 +… =1+z+z + (z +z )²/2+(z+z)³/6+… .

2n

1

4

-z²/2!+z /4!-…+(-1)ⁿ z /(2n)!+…=cos z (3)

z

5

2n+1

-z³/3!+z /5!-…+(-1)ⁿz /(2n+1)!+…=sin z (4)

c

z

os(-z)=cos(z), sin(-z)=-sinz

e

-z

=1+z+z²/2!+z³/3!+…

e =1-z+z²/2!-z³/3!+…

z

-z

c

z

-z

h z=(e +e )/2 (5)

s

4

h z=(e –e )/2 (6)

c

5

h z=1+z²/2!+z /4!+… (7)

s

iz

4

5

5

4

h z=z+z³/3!+z /5!+… (8)

e

5

4

iφ

=1+iz+(iz)²/2!+(iz)³/3!+(iz) /4!+(iz) /5!+…=1+iz-z²/2!-iz³/3!+z /4!+iz /5! +… =(1-z²/2!+z /4!-…)+i(z-z³/3!+z /5!-…)=cos z + i∙sin z (формула Эйлера)

φ

z

x+iy

x

iy

x

ЄR, e =cos φ+isin φ

e

iz

= e =e ∙e =e (cos y+isin y)

e

-iz

=cos z +isin z (*)

e

iz

-iz

=cos (-z)+isin (-z)=cos z-isin z (**)

c

-iz

iz-

os z=(e +e )/2 (9)

sin z=(e -e )/2 (10)

ch iz=cos z cos iz=ch z

shi z=isin z sin iz=ish z

cos²z+sin²z=1 ch²z-sh²z=1

_

c

1

2

1

1

2

2

os ( z ±z )=cos z cos z +sin z sin z

s

1

1

1

2

2

2

in ( z ±z )=sin z cos z ± cos z sin z

c

1

1

1

1

1

1

2

2

2

2

2

2

h (z±z )=ch z ch z ±sh z sh z sh (z ±z )= sh z ch z ±ch z sh z