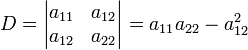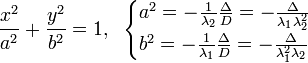- •Перелік питань до іспиту з «Алгебри та геометрії» для студентів 1 курсу спец. «комп’ютерна інженерія» 2014-2015 н.Р.
- •Свойства определителей
- •Треугольные матрицы
- •Диагональные матрицы
- •2.10. Приведение матрицы к диагональному виду
- •Ступенчатая матрица
- •Алгоритм приведения матрицы к ступенчатому виду
- •Свойства Инвариантность ранга при элементарных преобразованиях
- •Эквивалентность слау при элементарных преобразованиях
- •Нахождение обратных матриц
- •Ступенчатый вид по строкам
- •Определитель произведения матриц Теорема 2.2 об определителе произведения матриц
- •Обратная матрица
- •Замечание
- •Свойства обратной матрицы:
- •Матричные уравнения
- •Понятие комплексного числа
- •Действительная и мнимая часть комплексного числа
- •Мнимая единица
- •Равные комплексные числа
- •1.2.Тригонометрическая форма комплексного числа.
- •Формулы для многочленов и операции над многочленами
- •2. Деление с остатком. Теорема Безу
- •Нахождение нод по алгоритму Евклида и с помощью разложения на простые множители.
- •Алгоритм Евклида для нахождения нод
- •Нахождение нод с помощью разложения чисел на простые множители
- •Нахождение нод трех и большего количества чисел
- •Нахождение нод отрицательных чисел
- •Кратные корни многочленов
- •Метод Штурма отделения корней многочлена
- •Способы разложения на множители многочлена степени выше второй.
- •Вынесение за скобки общего множителя.
- •Разложение на множители многочлена с рациональными корнями.
- •Гипотеза h
- •Формулировка
- •Частные случаи
- •*4. Основная теорема алгебры
- •Линейные пространства: определение и примеры Аксиомы линейного пространства
- •Следствия аксиом линейного пространства
- •Примеры линейных пространств
- •Изоморфизм линейных пространств
- •Пересечение и сумма подпространств линейного пространства
- •Прямая сумма подпространств
- •Признаки прямых сумм подпространств
- •Формулы скалярного произведения векторов заданных координатами
- •Примеры задач на вычисление скалярного произведения векторов Примеры вычисления скалярного произведения векторов для плоских задач
- •Пример вычисления скалярного произведения векторов для пространственных задач
- •Пример вычисления скалярного произведения для n -мерных векторов
- •Векторное произведение векторов и его свойства
- •Алгебраические свойства векторного произведения
- •Геометрические свойства векторного произведения
- •Выражение векторного произведения через координаты векторов
- •Формула вычисления векторного произведения
- •Определение смешанного произведения.
- •Смешанное произведение в координатной форме.
- •Свойства смешанного произведения.
- •Вычисление смешанного произведения, примеры и решения.
- •Геометрический смысл смешанного произведения.
- •Необходимое и достаточное условие компланарности трех векторов.
- •Уравнение поверхности
- •Уравнение прямой по точке и вектору нормали
- •Уравнение прямой, проходящей через две точки
- •Уравнение прямой по точке и угловому коэффициенту
- •Уравнение прямой по точке и направляющему вектору
- •Уравнение прямой в отрезках
- •Нормальное уравнение прямой
- •Угол между прямыми на плоскости
- •Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой
- •Расстояние от точки до прямой
Угол между прямыми на плоскости
|
|
 .
.
Две прямые параллельны, если k1 = k2 . Две прямые перпендикулярны, если k1 = -1/ k2 .
Теорема. Прямые Ах + Ву + С = 0 и А 1 х + В1 у + С1 = 0 параллельны, когда пропорциональны коэффициенты А1 = λА, В1 = λВ. Если еще и С1 = λС, то прямые совпадают. Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых.
Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой
Определение. Прямая, проходящая через точку М1 (х1 , у1 ) и перпендикулярная к прямой у = kx + b представляется уравнением:

Расстояние от точки до прямой
Теорема. Если задана точка М(х0 , у0 ), то расстояние до прямой Ах + Ву + С =0 определяется как
 .
.
Доказательство. Пусть точка М 1(х 1, у 1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М1 :
![]() (1)
(1)
Координаты x1 и у1 могут быть найдены как решение системы уравнений:
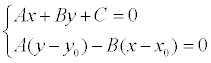
Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М 0 перпендикулярно заданной прямой. Если преобразовать первое уравнение системы к виду:
A(x – x 0 ) + B(y – y0 ) + Ax0 + By0 + C = 0,
то, решая, получим:
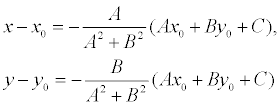
Подставляя эти выражения в уравнение (1), находим:

Теорема доказана.
Пример. Определить угол между прямыми: y = -3 x + 7; y = 2 x + 1.
k 1 =
-3; k 2 =
2; tgφ =  ;
φ= p /4.
;
φ= p /4.
Пример. Показать, что прямые 3х – 5у + 7 = 0 и 10х + 6у – 3 = 0 перпендикулярны.
Решение. Находим: k 1 = 3/5, k2 = -5/3, k 1* k 2 = -1, следовательно, прямые перпендикулярны.
Пример. Даны вершины треугольника А(0; 1), B (6; 5), C (12; -1). Найти уравнение высоты, проведенной из вершины С.
Решение.
Находим уравнение стороны АВ:  ;
4 x = 6 y – 6;
;
4 x = 6 y – 6;
2 x –
3 y + 3 = 0; 
Искомое
уравнение высоты имеет вид: Ax + By + C = 0
или y = kx + b . k = ![]() .
Тогда y =
.
Тогда y =  .
Т.к. высота проходит через точку С, то
ее координаты удовлетворяют данному
уравнению:
.
Т.к. высота проходит через точку С, то
ее координаты удовлетворяют данному
уравнению: 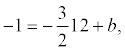 откуда
b = 17. Итого: .
откуда
b = 17. Итого: .
Ответ: 3 x + 2 y – 34 = 0.
Криві та поверхні другого порядку. Канонічні рівняння кривих другого порядку (еліпс, коло, гіпербола, парабола). Їх властивості.
|
Кривые второго порядка. Канонический вид уравнений второго порядка. |
| |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
Типові практичні завдання.
Знайти загальний розв’язок неоднорідної системи лінійних рівнянь за методом Гауса

Обчислити комплексні корені:
 .
.Знайти ГМТ:
 .
.З’ясувати, чи є вектор
 лінійною комбінацією векторів
лінійною комбінацією векторів ?
?
![]() .
.
Знайти ранг системи векторів, базу та подати решту векторів у вигляді лінійної комбінації векторів з цієї бази
 ,
, .
.Обчислити визначник:
 .
.Обчислити значення многочлена

 від
матриці
від
матриці .
.
Просто заменить Х на матрицу со всеми вытекающими
Знайти обернену матрицю до матриці
 .
.
Знайти загальний розв’язок неоднорідної системи лінійних рівнянь та фундаментальну систему розв’язків відповідної однорідної СЛР.
 .
.
Знайти ранг матриці в залежності від значення параметру
 .
.
 .
.
Знайти найбільший спільний дільник многочленів
 і
і .
.Визначити кратність кореня
 многочлена
многочлена
 .
.Відділити кратні корені многочлена

Побудувати многочлен найменшого степеня, який має корінь (-1) кратності 2; корені 3, 2-i,I- прості, якщо коефіцієнти цього многочлена – дійсні, комплексні.
Найти базисы суммы и пересечения подпространств
 та
та .
.Доказать, что многочлены
 создают базис простору
создают базис простору ,
если
,
если .
.Доказать, что каждая из двух систем векторов создает базис, и построить матрицу перехода к базису Е к Е´, где
Е:
![]() ,
,![]() ,
,![]() ;
Е´:
;
Е´:![]() ,
,![]() ,
,![]() .
.
Рассмотрим плоскость
 .
.
- Найти
расстояние от
![]() к плоскости;
к плоскости;
- Составить
уравнение плоскости, которая проходит
через А параллельно плоскости![]() .
.
Известны координаты вершин тетраэдра
 .
-
Вычислить объем тетраэдра
- Составить
общее уравнениеодной
грани
и каноническое уравнение одного ребра
тетраэдра.
- Вычислить площадь АВС.
.
-
Вычислить объем тетраэдра
- Составить
общее уравнениеодной
грани
и каноническое уравнение одного ребра
тетраэдра.
- Вычислить площадь АВС.