
- •Перелік питань до іспиту з «Алгебри та геометрії» для студентів 1 курсу спец. «комп’ютерна інженерія» 2014-2015 н.Р.
- •Свойства определителей
- •Треугольные матрицы
- •Диагональные матрицы
- •2.10. Приведение матрицы к диагональному виду
- •Ступенчатая матрица
- •Алгоритм приведения матрицы к ступенчатому виду
- •Свойства Инвариантность ранга при элементарных преобразованиях
- •Эквивалентность слау при элементарных преобразованиях
- •Нахождение обратных матриц
- •Ступенчатый вид по строкам
- •Определитель произведения матриц Теорема 2.2 об определителе произведения матриц
- •Обратная матрица
- •Замечание
- •Свойства обратной матрицы:
- •Матричные уравнения
- •Понятие комплексного числа
- •Действительная и мнимая часть комплексного числа
- •Мнимая единица
- •Равные комплексные числа
- •1.2.Тригонометрическая форма комплексного числа.
- •Формулы для многочленов и операции над многочленами
- •2. Деление с остатком. Теорема Безу
- •Нахождение нод по алгоритму Евклида и с помощью разложения на простые множители.
- •Алгоритм Евклида для нахождения нод
- •Нахождение нод с помощью разложения чисел на простые множители
- •Нахождение нод трех и большего количества чисел
- •Нахождение нод отрицательных чисел
- •Кратные корни многочленов
- •Метод Штурма отделения корней многочлена
- •Способы разложения на множители многочлена степени выше второй.
- •Вынесение за скобки общего множителя.
- •Разложение на множители многочлена с рациональными корнями.
- •Гипотеза h
- •Формулировка
- •Частные случаи
- •*4. Основная теорема алгебры
- •Линейные пространства: определение и примеры Аксиомы линейного пространства
- •Следствия аксиом линейного пространства
- •Примеры линейных пространств
- •Изоморфизм линейных пространств
- •Пересечение и сумма подпространств линейного пространства
- •Прямая сумма подпространств
- •Признаки прямых сумм подпространств
- •Формулы скалярного произведения векторов заданных координатами
- •Примеры задач на вычисление скалярного произведения векторов Примеры вычисления скалярного произведения векторов для плоских задач
- •Пример вычисления скалярного произведения векторов для пространственных задач
- •Пример вычисления скалярного произведения для n -мерных векторов
- •Векторное произведение векторов и его свойства
- •Алгебраические свойства векторного произведения
- •Геометрические свойства векторного произведения
- •Выражение векторного произведения через координаты векторов
- •Формула вычисления векторного произведения
- •Определение смешанного произведения.
- •Смешанное произведение в координатной форме.
- •Свойства смешанного произведения.
- •Вычисление смешанного произведения, примеры и решения.
- •Геометрический смысл смешанного произведения.
- •Необходимое и достаточное условие компланарности трех векторов.
- •Уравнение поверхности
- •Уравнение прямой по точке и вектору нормали
- •Уравнение прямой, проходящей через две точки
- •Уравнение прямой по точке и угловому коэффициенту
- •Уравнение прямой по точке и направляющему вектору
- •Уравнение прямой в отрезках
- •Нормальное уравнение прямой
- •Угол между прямыми на плоскости
- •Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой
- •Расстояние от точки до прямой
Формулы для многочленов и операции над многочленами
Напомним какое выражение называется многочленом.
Одночленом
степени ![]() (здесь
(здесь ![]() )
называется следующее выражение
)
называется следующее выражение
![]()
где ![]() --
коэффициент,
--
коэффициент, ![]() -
переменная.
-
переменная.
Многочленом ![]() -
ой степени (здесь
-
ой степени (здесь ![]() )
с вещественными коэффициентами
)
с вещественными коэффициентами![]() называется
следующее выражение:
называется
следующее выражение:
![]()
здесь ![]() -
переменная. Можно сказать, что многочлен
- это линейная комбинация одночленнов
разных степеней.
-
переменная. Можно сказать, что многочлен
- это линейная комбинация одночленнов
разных степеней.
Операции над многочленами:
Пусть ![]() два
многочлена степени
два
многочлена степени ![]() и
и ![]() соответственно,
т.е.
соответственно,
т.е.
![]()
![]()
предположим,
что ![]() .
.
Сумма и разность многочленов:
 .
.
Суммой
и разностью многочленов ![]() и
и ![]() называется
следующий многочлен:
называется
следующий многочлен:
![]()
![]()
Степень
полученного многочлена ![]() не
превосходит максимальной степени
многочленов
не
превосходит максимальной степени
многочленов ![]() и
и ![]() .
.
Умножение на одночлен:
 .
.
Умножим
одночлен ![]() на
многочлен
на
многочлен ![]() :
:
![]()
![]()
т.е. каждый член многочлена умножается на одночлен. Здесь применяем правило работы со степенями.
Умножение многочленов:
 .
.
Умножим
многочлен ![]() на
на ![]() :
:
![]()
![]()
![]()
В
итоге свели операцию умножения многочленов
к умножению одночлена на многочлен.
Заметим, что при умножении многочленов
степени ![]() и
и ![]() получается
многочлен степени
получается
многочлен степени ![]() .
При умножении многочленов необходимо
каждый член одного многочлена умножить
на каждый член другого многочлена.
.
При умножении многочленов необходимо
каждый член одного многочлена умножить
на каждый член другого многочлена.
Деление многочленов:
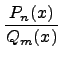 .
.
Разделим
многочлен ![]() на
на ![]() ,
т.е. представим выражение
,
т.е. представим выражение  в
следующем виде:
в
следующем виде:

где ![]() --
частное от деления,
--
частное от деления, ![]() --
делимое,
--
делимое, ![]() --
делитель,
--
делитель, ![]() --
остаток.
--
остаток.
При
делении многочлена ![]() на
многочлен
на
многочлен ![]() ,
где
,
где ![]() ,
нужно найти многочлены
,
нужно найти многочлены ![]() и
и ![]() такие,
чтобы выполнялось равенство
такие,
чтобы выполнялось равенство
![]()
Существует много способов поиска таких многочленов. В основном используются школьные способы, а именно, деление "уголком" ("столбиком") и метод неопределенных коэффициентов (будут рассмотрены ниже).
2. Деление с остатком. Теорема Безу
Деление с остатком
Определение.Пусть![]() и
и![]() —многочлены,
—многочлены,![]() .
Будем говорить, что
.
Будем говорить, что![]() поделен
на
поделен
на![]() с
остатком, если
с
остатком, если![]() представлен
в виде
представлен
в виде![]() ,
где
,
где![]() и
и![]() —
многочлены, причем
—
многочлены, причем![]() .
.
Полином ![]() называется
остатком от деления
называется
остатком от деления![]() на
на![]() ,
,![]() —
неполным частным.
—
неполным частным.
Пример.![]() .
.
![]() .
.
Теорема.(о
делении с остатком). Пусть![]() и
и![]() —
полиномы над полем
—
полиномы над полем![]() ,
,![]() .
Тогда существуют единственные
многочлены
.
Тогда существуют единственные
многочлены![]() и
и![]() над
полем
над
полем![]() такие,
что
такие,
что![]() и
и![]() .
.
Доказательство.Существование.
Пусть ![]() .Положим
.Положим![]() .
.
![]() .
.
Предположим,
что теорема верна не для любого
полинома ![]() (
(![]() фиксируем).
Среди всех многочленов
фиксируем).
Среди всех многочленов![]() ,
для которых теорема неверна, выберем
многочлен наименьшей степени и обозначим
его
,
для которых теорема неверна, выберем
многочлен наименьшей степени и обозначим
его![]() :
:
![]()
Пусть ![]() .
Положим
.
Положим
![]()
Коэффициент
при ![]() в
многочлене
в
многочлене![]() равен
равен![]() .
Следовательно,
.
Следовательно,![]() .
Значит, для многочлена
.
Значит, для многочлена![]() теорема
верна. Существуют такие
теорема
верна. Существуют такие![]() и
и![]() ,
что
,
что![]() .
Тогда
.
Тогда

Получили противоречие с тем предположением, что есть многочлены, для которых теорема неверна.
Единственность.
Предположим, что

1) ![]() .
Значит,
.
Значит,![]() ,
,
2) ![]() .
.
![]() Получили
противоречие. Этот случай невозможен.
Получили
противоречие. Этот случай невозможен.
Теорема Безу
Теорема.Остаток
от деления многочлена![]() на
многочлен
на
многочлен![]() равен
равен![]() .
.
Доказательство.Степень
остатка меньше 1, следовательно, остаток
— константа. Пусть![]() —
остаток.
—
остаток.
![]()
Это
равенство верно при любых
значениях ![]() .Положим
.Положим![]() :
:![]()
Задачи.
1. Проверьте, выполняются ли условия:
1) ![]() делится
на
делится
на![]() ;
;
2)![]() делится
на
делится
на![]() .
.
2.Докажите, что
![]() делится
на
делится
на ![]() .
.
3.Найдите
значения параметров![]() и
и![]() ,
при которых
,
при которых
![]() делится
на
делится
на ![]() .
.
4.Найдите
все значения параметров![]() и
и![]() ,
такие, что остаток от деления
,
такие, что остаток от деления
![]() на
на ![]() равен
равен![]() .
.
5.Найдите
все натуральные![]() ,
такие, что
,
такие, что
![]() делится
на
делится
на ![]() .
.
6.Известно,
что остаток от деления полинома![]() на
на![]() равен
2, от деления
равен
2, от деления![]() на
на![]() равен
1. Найдите остаток от деления
равен
1. Найдите остаток от деления![]() на
на![]() .
.
7.Найдите
остаток от деления многочлена![]() на
на![]() .
.
8.Полином![]() с
целыми коэффициентами принимает значение
5 в пяти различных целых точках. Может
ли он иметь целый корень?
с
целыми коэффициентами принимает значение
5 в пяти различных целых точках. Может
ли он иметь целый корень?
Комментарии(RSS) |Трекбек
Відношення подільності. Схема Горнера.
Схема Горнера.
Схема Горнера– это алгоритм деления (деление схемой Горнера) многочленов, записываемый для
частного случая,
если частное равно двучлену ![]() .
.
Построим этот алгоритм:
Предположим,
что ![]() -
делимое
-
делимое
![]() -
частное (его степень, вероятно, будет
на удиницу меньше),
-
частное (его степень, вероятно, будет
на удиницу меньше),
r- остаток (т.к. деление осуществляется на многочлен1-ойстепени, то степень остатка будет на
единицу меньше, т.е. нулевая, таким образом, остаток это константа).
По определению деления с остатком P(x) = Q(x) (x–a) + r. После подстановки выражений многочленов
получаем:
![]()
Раскрываем скобки и приравниваем коэффициенты при одинаковых степенях, после чего выражаем
коэффициенты частного через коэффициенты делимого и делителя:

Удобно вычисления сводить в такую таблицу:

В ней выделены те клетки, содержимое которых участвует в вычислениях на очередном шаге.
Схема Горнера примеры:
Пусть
надо поделить многочлен ![]() на
двучленx–2.
на
двучленx–2.
Составляем таблицу с двумя строками. В 1 строку выписываем коэффициенты нашего многочлена. Во
второй строке будем получать коэффициенты неполного частного по следующей схеме: в первую очередь
переписываем старший коэффициент данного многочлена, далее, дабы получить очередной коэффициент,
умножаем последний найденный на а=2и складываем с соответствующим коэффициентом
многочлена F(x). Самый последний коэффициент будет остатком, а все предыдущие – коэффициентами
неполного частного.
![]()

Найбільший спільний дільник (НСД). Алгоритм Евкліда.
