Алгоритм приведения матрицы к ступенчатому виду

Чтобы привести матрицу к ступенчатому виду (рис. 1.4), нужно выполнить следующие действия.

1. В первом столбце выбрать элемент, отличный от нуля (ведущий элемент). Строку с ведущим элементом (ведущая строка), если она не первая, переставить на место первой строки (преобразование I типа). Если в первом столбце нет ведущего (все элементы равны нулю), то исключаем этот столбец, и продолжаем поиск ведущего элемента в оставшейся части матрицы. Преобразования заканчиваются, если исключены все столбцы или в оставшейся части матрицы все элементы нулевые.

2. Разделить все элементы ведущей строки на ведущий элемент (преобразование II типа). Если ведущая строка последняя, то на этом преобразования следует закончить.

3. К каждой строке, расположенной ниже ведущей, прибавить ведущую строку, умноженную соответственно на такое число, чтобы элементы, стоящие под ведущим оказались равными нулю (преобразование III типа).

4. Исключив из рассмотрения строку и столбец, на пересечении которых стоит ведущий элемент, перейти к пункту 1, в котором все описанные действия применяются к оставшейся части матрицы.

7. Теорема про розклад визначника по елементам рядка.

Теорема о разложении определителя по элементам строки или столбца позволяет свести вычисление определителя - го порядка () к вычислению определителей порядка.

Если определитель имеет равные нулю элементы, то удобнее всего разлагать определитель по элементам той строки или столбца, который содержит наибольшее число нулей.

Используя свойства определителей, можно преобразовать определитель - го порядка так, чтобы все элементы некоторой строки или столбца, кроме одного, стали равными нулю. Таким образом, вычисление определителя- го порядка, если он отличен от нуля, сведется к вычислению одного определителя-го порядка.

Задача 3.1. Вычислить определитель

.

Решение.Прибавив ко второй строке первую, к третьей – первую, умноженную на 2, к четвертой – первую, умноженную на -5, получим

.

Разлагая определитель по элементам первого столбца, имеем

.

В полученном определителе 3-го порядка обратим в нуль все элементы первого столбца, кроме первого. Для этого ко второй строке прибавим первую, умноженную на (-1), к третьей, умноженной на 5, прибавим первую, умноженную на 8. Так как умножали третью строку на 5, то (для того, чтобы определитель не изменился) умножим его на . Имеем

.

Полученный определитель разложим по элементам первого столбца:

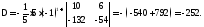
8. Теорема Лапласа(1). Теорема про чужі доповнення(2)

1)Определитель равен сумме произведений элементов какой-либо строки на их алгебраические дополнения.

2)Сумма произведений элементов какой-либо строки определителя на алгебраические дополнения соответствующих элементов другой его строки равна нулю (теорема об умножении на чужие алгебраические дополнения).

9. Арифметичні векторні простори.

Всякая точка на плоскости при выбранной системе координат задается парой (α, β) своих координат; числа α и β можно понимать также как координаты радиуса-вектора с концом в этой точке. Аналогично, в пространстве тройка (α, β, γ) определяет точку или вектор с координатами α, β, γ. Именно на этом основывается хорошо известная читателю геометрическая интерпретация систем линейных уравнений с двумя или тремя неизвестными. Так, в случае системы двух линейных уравнений с двумя неизвестными

а₁х + b₁у = с₁,

а₂х + b₂у = с₂

каждое из уравнений истолковывается как прямая на плоскости (см. рис. 26), а решение (α, β) - как точка пересечения этих прямых или как вектор с координатами аир (рисунок соответствует случаю, когда система имеет единственное решение).

Рис. 26

Аналогично можно поступить с системой линейных уравнений с тремя неизвестными, интерпретируя каждое уравнение как уравнение плоскости в пространстве.

В математике и различных ее приложениях (в частности, в теории кодирования) приходится иметь дело с системами линейных уравнений, содержащих более трех неизвестных. Системой линейных уравнений с n неизвестными x₁, х₂, ..., х_n называется совокупность уравнений вида

а₁₁х₁ + а₁₂х₂ + ... + а_1nх_n = b₁,

а₂₁х₁ + а₂₂х₂ + ... + а_2nх_n = b₂,

. . . . . . . . . . . . . . . . . . . . . . (1)

а_m1х₁ + а_m2х₂ + ... + а_mnх_n = b_m,

где a_ij и b_i - произвольные действительные числа. Число уравнений в системе может быть любым и никак не связано с числом неизвестных. Коэффициенты при неизвестных а_ij имеют двойную нумерацию: первый индекс i указывает номер уравнения, второй индекс j - номер неизвестного, при котором стоит данный коэффициент.

Всякое решение системы понимается как набор (действительных) значений неизвестных (α₁, α₂, ..., α_n), обращающих каждое уравнение в верное равенство.

Хотя непосредственное геометрическое истолкование системы (1) при n > 3 уже невозможно, однако вполне возможно и во многих отношениях удобно распространить на случай произвольного n геометрический язык пространства двух или трех измерений. Этой цели и служат дальнейшие определения.

Всякий упорядоченный набор из n действительных чисел (α₁, α₂, ..., α_n) называется n-мерным арифметическим вектором, а сами числа α₁, α₂, ..., α_n - координатами этого вектора.

Для обозначения векторов используется, как правило, жирный шрифт и для вектора а с координатами α₁, α₂, ..., α_n сохраняется обычная форма записи:

а = (α₁, α₂, ..., α_n).

По аналогии с обычной плоскостью множество всех n-мерных векторов, удовлетворяющих линейному уравнению с n неизвестными, называют гиперплоскостью в n-мерном пространстве. При таком определении множество всех решений системы (1) есть не что иное, как пересечение нескольких гиперплоскостей.

Сложение и умножение n-мерных векторов определяются по тем же правилам, что и для обычных векторов. А именно, если

а = (α₁, α₂, ..., α_n), b = (β₁, β₂, ..., β_n) (2)

- два n-мерных вектора, то их суммой называется вектор

α + β = (α₁ + β₁, α₂ + β₂, ..., α_n + β_n). (3)

Произведением вектора а на число λ называется вектор

λа = (λα₁, λα₂, ..., λα_n). (4)

Множество всех n-мерных арифметических векторов с операциями сложения векторов и умножения вектора на число называется арифметическим n-мерным векторным пространством L_n.

Используя введенные операции, можно рассматривать произвольные линейные комбинации нескольких векторов, т. е. выражения вида

λ₁a₁ + λ₂a₂ + ... + λ_ka_k,

где λ_i - действительные числа. Например, линейная комбинация векторов (2) с коэффициентами λ и μ - это вектор

λа + μb = (λα₁ + μβ₁, λα₂ + μβ₂, ..., λα_n + μβ_n).

В трехмерном пространстве векторов особую роль играет тройка векторов i, j, k (координатные орты), по которым разлагается любой вектор а:

a = xi + yj + zk,

где х, у, z - действительные числа (координаты вектора а).

В n-мерном случае такую же роль играет следующая система векторов:

e₁ = (1, 0, 0, ..., 0),

e₂ = (0, 1, 0, ..., 0),

e₃ = (0, 0, 1, ..., 0),

. . . . . . . . . . . . (5)

e_n = (0, 0, 0, ..., 1).

Всякий вектор а есть, очевидно, линейная комбинация векторов е₁, e₂, ..., e_n:

а = а₁е₁ + а₂е₂ + ... + а_nе_n, (6)

причем коэффициенты α₁, α₂, ..., α_n совпадают с координатами вектора а.

Обозначая через 0 вектор, все координаты которого равны нулю (кратко, нулевой вектор), введем следующее важное определение:

Система векторов а₁, а₂, ..., а_k называется линейно зависимой, если существует равная нулевому вектору линейная комбинация

λ₁a₁ + λ₂a₂ + ... + λ_ka_k = 0,

в которой хотя бы один из коэффициентов h₁, λ₂, ..., λ_k отличен от нуля. В противном случае система называется линейно независимой.

Так, векторы

а₁ = (1, 0, 1, 1), а₂ = (1, 2, 1, 1), а₃ = (2, 2, 2, 2)

линейно зависимы, поскольку

a₁ + a₂ - а₃ = 0.

Линейная зависимость, как видно из определения, равносильна (при k ≥ 2) тому, что хотя бы один из векторов системы является линейной комбинацией остальных.

Если система состоит из двух векторов a₁, а₂, то линейная зависимость системы означает, что один из векторов пропорционален другому, скажем, а₁ = λа₂; в трехмерном случае это равносильно коллинеарности векторов а₁ и а₂. Точно так же линейная зависимость системы I из трех векторов в обычном пространстве означает компланарность этих векторов. Понятие линейной зависимости является, таким образом, естественным обобщением понятий коллинеарности и компланарности.

Нетрудно убедиться, что векторы е₁, е₂, ..., е_n из системы (5) линейно независимы. Следовательно, в n-мерном пространстве существуют системы из n линейно независимых векторов. Можно показать, что всякая система из большего числа векторов линейно зависима.

Всякая система a₁, а₂, ..., а_n из n линейно независимых векторов n-мерного пространства L_n называется его базисом.

Любой вектор а пространства L_n раскладывается, и притом единственным образом, по векторам произвольного базиса a₁, а₂, ..., а_n:

а = λ₁a₁ + λ₂a₂ + ... + λ_na_n.

Этот факт легко устанавливается на основании определения базиса.

Продолжая аналогию с трехмерным пространством, можно и в n-мерном случае определить скалярное произведение а · b векторов, полагая

a · b = α₁β₁ + α₂β₂ + ... + α_nβ_n.

При таком определении сохраняются все основные свойства скалярного произведения трехмерных векторов. Векторы а и b называются ортогональными, если их скалярное произведение равно нулю:

α₁β₁ + α₂β₂ + ... + α_nβ_n = 0.

В теории линейных кодов используется еще одно важное понятие - понятие подпространства. Подмножество V пространства L_nназывается подпространством этого пространства, если

1) для любых векторов а, b, принадлежащих V, их сумма а + b также принадлежит V;

2) для любого вектора а, принадлежащего V, и для любого действительного числа λ вектор λа также принадлежит V.

Например, множество всех линейных комбинаций векторов e₁, е₂ из системы (5) будет подпространством пространства L_n.

В линейной алгебре доказывается, что во всяком подпространстве V существует такая линейно независимая система векторов a₁, a₂, ..., a_k, что всякий вектор а подпространства является линейной комбинацией этих векторов:

a = λ₁a₁ + λ₂a₂ + ... + λ_ka_k.

Указанная система векторов называется базисом подпространства V.

Из определения пространства и подпространства непосредственно следует, что пространство L_n есть коммутативная группа относительно операции сложения векторов, а любое его подпространство V является подгруппой этой группы. В этом смысле можно, например, рассматривать смежные классы пространства L_n по подпространству V.

В заключение подчеркнем, что если в теории n-мерного арифметического пространства вместо действительных чисел (т. е. элементов поля действительных чисел) рассматривать элементы произвольного поля F, то все определения и факты, приведенные выше, сохранили бы силу.

В теории кодирования важную роль играет случай, когда поле F поле вычетов Z_p, которое, как мы знаем, конечно. В этом случае соответствующее n-мерное пространство также конечно и содержит, как нетрудно видеть, рⁿ элементов.

Понятие пространства, как и понятия группы и кольца, допускает также и аксиоматическое определение. За подробностями мы отсылаем Питателя к любому курсу линейной алгебры.

10. Лінійна комбінація. Лінійно залежні та незалежні системи векторів.

инейная комбинация векторов

     Линейной комбинацией векторов называют вектор

     

где - коэффициенты линейной комбинации. Есликомбинация называется тривиальной, если- нетривиальной.

     Линейная зависимость и независимость векторов

     Система линейно зависимачто

     Система линейно независима

     Критерий линейной зависимости векторов

     Для того чтобы векторы (r > 1) были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из этих векторов являлся линейной комбинацией остальных.

     Размерность линейного пространства

     Линейное пространство Vназываетсяn-мерным (имеет размерностьn), если в нем:

     1) существует nлинейно независимых векторов;

     2) любая система n + 1векторов линейно зависима.

     Обозначения : n= dimV;.

Система векторов называетсялинейно зависимой,если существуетненулевой наборчиселтаких, что линейная комбинация

.

Система векторов называетсялинейно независимой,если из равенства нулю линейной комбинации

следует равенство нулювсех коэффициентов

Вопрос о линейной зависимости векторов в общем случае сводится к вопросу о существовании ненулевого решения у однородной системы линейных уравнений с коэффициентами, равными соответствующим координатам данных векторов.

Для того чтобы хорошо усвоить понятия «линейная зависимость», «линейная независимость» системы векторов, полезно решить задачи следующего типа:

11. Лінійна залежність.І і ІІ критерії лінійної залежності.

Система векторов линейно зависима тогда и только тогда, когда один из векторов системы является линейной комбинацией остальных векторов этой системы.

        Доказательство.     Пусть система векторов линейно зависима. Тогда существует такой набор коэффициентов , что , причем хотя бы один коэффициент отличен от нуля. Предположим, что . Тогда

то есть является линейной комбинацией остальных векторов системы.

Пусть один из векторов системы является линейной комбинацией остальных векторов. Предположим, что это вектор , то есть . Очевидно, что . Получили, что линейная комбинация векторов системы равна нулю, причем один из коэффициентов отличен от нуля (равен ).      

        Предложение 10.7   Если система векторов содержит линейно зависимую подсистему, то вся система линейно зависима.

        Доказательство.    

Пусть в системе векторов подсистема , , является линейно зависимой, то есть , и хотя бы один коэффициент отличен от нуля. Тогда составим линейную комбинацию . Очевидно, что эта линейная комбинация равна нулю, и что среди коэффициентов есть ненулевой.      

12. База системи векторів, її основна властивість.

Базой ненулевой системы векторов называется эквивалентная ей линейно независимая подсистема. Нулевая система базы не имеет.

Свойство 1: База линейной независимой системы совпадает с ней самой.

Пример:  Система линейно независимых векторов поскольку ни один из векторов не может быть линейно вырожен через остальные.

Свойство 2:(Критерий Базы) Линейно независимая подсистема данной системы является её базой тогда и только тогда, когда она максимально линейно независима.

Доказательство: Дана система  Необходимость Пусть база . Тогда по определению и, если , где , система линейно зависима, так как линейно вырожается через , следовательно максимально линейно независима. Достаточность Пусть максимально линейно независимая подсистема, тогда   где .  линейно зависима линейно вырожается через следовательно база системы .

Свойство 3:(Основное свойство базы) Каждый вектор системы вырожается через базу единственным образом.

Доказательство Пусть вектор вырожается через базу двумя способами,  тогда: , тогда    

13. Ранг системи векторів.

Определение: Рангом ненулевой системы векторов линейного пространства называется число векторов её базы. Ранг нулевой системы по определению равен нулю.

Свойства ранга: 1) Ранг линейно независимой системы совпадает с числом её векторов. 2) Ранг линейно зависимой системы меньше числа её векторов. 3) Ранги эквивалентных систем совпадают —rankrank. 4) Ранг под системы меньше либо равен рангу системы. 5) Еслии rankrank, тогдаиимеют общую базу. 6) Ранг системы не изменить, если в неё добавить вектор, являющийся линейной комбинацией остальных векторов системы. 7) Ранг системы не изменить, если из неё удалить вектор, являющийся линейной комбинацией остальных векторов.

Для нахождения ранга системы векторов, нужно использовать метод Гауссаи привести систему к треугольной или трапециевидной форме.

14. Еквівалентні системи векторів.

Пример:

Преобразуем данные вектора в матрицу для нахождения базы. Получим:

Теперь при помощи метода Гаусса будем преобразоывавать матрицу к трапецеидальному виду:

1) В нашей основной матрице, будем анулировать весь первый столбец кроме первой строки  от второй отнимим первую умноженную на , от третьей отнимим первую умноженную на , а от четвётой мы ничего не будем отнимать так как первый элемент четвёртой строки, то есть пересечение первого столбца и четвёртой строки, равен нулю. Получим матрицу : 2) Теперь в матрице , поменяем местами строки 2, 3 и 4 для простоты решения, что бы на месте элемента была еденица. Четвёртую строку поменяем поставим вместо второй, вторую вместо третьей и третью на место четвёртой. Получим матрицу : 3)В матрице анулируем все элементы под элементом . Поскольку вновь элемент нашей матреци равен нулю, мы ничего не отнимаем от четвёртой строки, а к третьей добавим вторую умноженную на . Получим матрицу : 4)Вновь поменяем в матрице строки 3 и 4 местами. Получим матрицу : 5)В матрицеприбавим к червётрой строке третью, умноженную на 5. Получим матрицу, которая будет иметь треугольный вид:

Системы , их ранги совпадают в силу свойств ранга и их ранг равен rank rank

Замечания: 1) В отличие от традиционного метода Гаусса, если в строке матрицы все элементы делятся на определённое число, мы не имеем право сокращать строку матрицы в силу действия свойств матрицы. Если мы захотим сократить строку на определённое число, придётся сокращать всю матрицу на это число. 2) В случае, если мы получим линейно зависящую строку, мы можем её убрать из нашей матрицы и заменить на нулевую строку. Пример: Сразу видно что вторая строка выражается через первую, если домножить первую на 2. В тиаком случае можем заменить всю вторую строку на нулевую. Получим: В итоге, приведя матрицу, либо к треугольному, либо к трапецеидальному виду, где у неё нету линейно зависящих векторов, все не нулевые векторы матрицы и будут базой матрицы, а их количество рангом.

Вот так же пример системы векторов в виде графика: Дана система где , , и . Базой данной системы очевидно буду вектора и , поскольку через них выражаются векторы . Данная система в графическом виде будет иметь вид:

15. Елементарні перетворення. Системи ступінчатого виду.

Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.

Элементарными преобразованиями строк называют:

• перестановку местами любых двух строк матрицы;

• умножение любой строки матрицы на константу 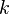, , при этом определитель матрицы увеличивается в k раз;

• прибавление к любой строке матрицы другой строки.

В некоторых курсах линейной алгебры перестановка строк матрицы не выделяется в отдельное элементарное преобразование в силу того, что перестановку местами любых двух строк матрицы можно получить, используя умножение любой строки матрицы на константу , и прибавление к любой строке матрицы другой строки, умноженной на константу , .

Аналогично определяются элементарные преобразования столбцов.

Элементарные преобразования обратимы.

Обозначение указывает на то, что матрица может быть получена из путём элементарных преобразований (или наоборот).