
- •Перелік питань до іспиту з «Алгебри та геометрії» для студентів 1 курсу спец. «комп’ютерна інженерія» 2014-2015 н.Р.
- •Свойства определителей
- •Треугольные матрицы
- •Диагональные матрицы
- •2.10. Приведение матрицы к диагональному виду
- •Ступенчатая матрица
- •Алгоритм приведения матрицы к ступенчатому виду
- •Свойства Инвариантность ранга при элементарных преобразованиях
- •Эквивалентность слау при элементарных преобразованиях
- •Нахождение обратных матриц
- •Ступенчатый вид по строкам
- •Определитель произведения матриц Теорема 2.2 об определителе произведения матриц
- •Обратная матрица
- •Замечание
- •Свойства обратной матрицы:
- •Матричные уравнения
- •Понятие комплексного числа
- •Действительная и мнимая часть комплексного числа
- •Мнимая единица
- •Равные комплексные числа
- •1.2.Тригонометрическая форма комплексного числа.
- •Формулы для многочленов и операции над многочленами
- •2. Деление с остатком. Теорема Безу
- •Нахождение нод по алгоритму Евклида и с помощью разложения на простые множители.
- •Алгоритм Евклида для нахождения нод
- •Нахождение нод с помощью разложения чисел на простые множители
- •Нахождение нод трех и большего количества чисел
- •Нахождение нод отрицательных чисел
- •Кратные корни многочленов
- •Метод Штурма отделения корней многочлена
- •Способы разложения на множители многочлена степени выше второй.
- •Вынесение за скобки общего множителя.
- •Разложение на множители многочлена с рациональными корнями.
- •Гипотеза h
- •Формулировка
- •Частные случаи
- •*4. Основная теорема алгебры
- •Линейные пространства: определение и примеры Аксиомы линейного пространства
- •Следствия аксиом линейного пространства
- •Примеры линейных пространств
- •Изоморфизм линейных пространств
- •Пересечение и сумма подпространств линейного пространства
- •Прямая сумма подпространств
- •Признаки прямых сумм подпространств
- •Формулы скалярного произведения векторов заданных координатами
- •Примеры задач на вычисление скалярного произведения векторов Примеры вычисления скалярного произведения векторов для плоских задач
- •Пример вычисления скалярного произведения векторов для пространственных задач
- •Пример вычисления скалярного произведения для n -мерных векторов
- •Векторное произведение векторов и его свойства
- •Алгебраические свойства векторного произведения
- •Геометрические свойства векторного произведения
- •Выражение векторного произведения через координаты векторов
- •Формула вычисления векторного произведения
- •Определение смешанного произведения.
- •Смешанное произведение в координатной форме.
- •Свойства смешанного произведения.
- •Вычисление смешанного произведения, примеры и решения.
- •Геометрический смысл смешанного произведения.
- •Необходимое и достаточное условие компланарности трех векторов.
- •Уравнение поверхности
- •Уравнение прямой по точке и вектору нормали
- •Уравнение прямой, проходящей через две точки
- •Уравнение прямой по точке и угловому коэффициенту
- •Уравнение прямой по точке и направляющему вектору
- •Уравнение прямой в отрезках
- •Нормальное уравнение прямой
- •Угол между прямыми на плоскости
- •Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой
- •Расстояние от точки до прямой
Свойства Инвариантность ранга при элементарных преобразованиях
|
|
Теорема
(об инвариантности ранга при
элементарных преобразованиях).
Если |
|
Эквивалентность слау при элементарных преобразованиях
Назовём элементарными преобразованиями над системой линейных алгебраических уравнений:
перестановку уравнений;
умножение уравнения на ненулевую константу;
сложение одного уравнения с другим, умноженным на некоторую константу.
То есть элементарные преобразования над её расширенной матрицей. Тогда справедливо следующее утверждение:
|
|
Теорема (об эквивалентности систем уравнений при элементарных преобразованиях). Система линейных алгебраических уравнений, полученная путём элементарных преобразований над исходной системой, эквивалентна ей. |
|
Напомним, что две системы называются эквивалентными, если множества их решений совпадают.
Нахождение обратных матриц
|
|
Теорема
(о нахождении обратной
матрицы).
Пусть определитель матрицы |
Ступенчатый вид по строкам
В линейной алгебре матрица считается матрицей ступенчатого вида по строкам если
все ненулевые строки (имеющие по крайней мере один ненулевой элемент) располагаются над всеми чисто нулевыми строками;
ведущий элемент (первый ненулевой элемент строки при отсчёте слева направо) каждой ненулевой строки располагается строго правее ведущего элемента в строке, расположенной выше данной.
Вот пример матрицы ступенчатого вида по строкам:

Матрица называется матрицей приведенного ступенчатого вида по строкам (или канонического вида по строкам) если она удовлетворяет дополнительному условию:
каждый ведущий элемент ненулевой строки - это единица, и он является единственным ненулевым элементом в своём столбце.
Вот пример матрицы приведенного ступенчатого вида по строкам:

Отметим, что левый край матрицы приведенного ступенчатого вида по строкам не обязательно имеет вид единичной матрицы. Например, следующая матрица является матрицей приведенного ступенчатого вида

поскольку константы в третьем столбце не являются ведущими элементами своих строк.
Розмір та базис простору
 .
.
Построение
базиса пространства, подпространства
несколько упрощается, если мы располагаем
некоторыми представлениями о размерности
пространства, подпространства. Одним
из наводящих соображений здесь может
быть следующее. Подмножество
 векторов пространства
векторов пространства выделяется из
выделяется из с помощью дополнительных условий,
накладываемых на векторы. При этом, чем
больше таких условий, тем меньшей, вообще
говоря, будет размерность подпространства
с помощью дополнительных условий,
накладываемых на векторы. При этом, чем
больше таких условий, тем меньшей, вообще
говоря, будет размерность подпространства .Если
.Если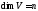 ,
а
,
а выделено с помощью
выделено с помощью условий специального вида, то есть
основания ожидать, что
условий специального вида, то есть
основания ожидать, что .
.
Матриці, дії над ними.
В матрице (1) числа называются её элементами (как и в определителе, первый индекс означает номер строки, второй – столбца, на пересечении которых стоит элемент; i = 1, 2, ..., m; j = 1, 2, n).
Матрица называется прямоугольной, если m не равно n
Если же m = n , то матрица называется квадратной, а число n – её порядком.
Матрицы называются равными, если у них одинаковое число строк и столбцов и все соответствующие элементы совпадают.
Матрица называется нулевой, если всё её элементы равны нулю. Нулевую матрицу будем обозначать символом 0 или 0mn
Матрицей-строкой (или строчной) называется 1n-матрица, а матрицей-столбцом (или столбцовой) – m1-матрица.
Матрица , которая получается из матрицы A заменой в ней местами строк и столбцов, называется транспонированной относительно матрицы A.
Операция перехода к матрице , транспонированной относительно матрицы A, называется транспонированием матрицы A . Для mn-матрицы транспонированной является nm-матрица.
Главной диагональюквадратной матрицы называется воображаемая линия, соединяющая её элементы, у которых оба индекса одинаковые. Эти элементы называютсядиагональными.
Квадратная матрица, у которой все элементы вне главной диагонали равны нулю, называется диагональной. Не обязательно все диагональные элементы диагональной матрицы отличны от нуля. Среди них могут быть и равные нулю.
Квадратная матрица, у которой элементы, стоящие на главной диагонали равны одному и тому же числу, отличному от нуля, а все прочие равны нулю, называется скалярной матрицей.
Единичной матрицей называется диагональная матрица, у которой все диагональные элементы равны единице.
Определителем квадратной матрицы A называется определитель, элементами которого являются элементы матрицы A . Он обозначается символом |A|.
Квадратная матрица называется неособенной (или невырожденной, несингулярной), если её определитель не равен нулю, и особенной (или вырожденной, сингулярной), если её определитель равен нулю.
Результатом операции умножение матрицы на число, результатом является произведение матрицы на число, результатом операции сложения (вычитания) матриц является сумма (разность) матриц.
Действия над матрицами
Для того, чтобы произвести умножение матрицы A на произвольное число α, нужно каждый из элементов матрицы A умножить на число α.
Свойства умножения матрицы на число
(здесь A, B - матрицы, - числа, 1 - число единица)
1дистрибут![]()
2 асоц
![]()
![]()
3.
18.
Асоціативність добутку матриць. Порушення
комутативності добутку матриць.Свойство
3. Произведение матриц некоммутативно,
т.е. AB not is BA ![]()
.Свойство 4. Произведение матриц ассоциативно, т.е. (АВ)С = А(ВС) .
Зведення матриці до діагонального виду. (смотретьвыше)
Ранги матриці. Теорема про ранг матриці.
Ранг матрицы
Ранг системы строк и столбцов матрицы
Определение
Рангом системы строкназывается максимальное количество линейно независимых строк этой системы.
В каждой матрице можно связать два ранга: строчный ранг (ранг системы строк) и столбцовый ранг (ранг системы столбцов).
Теорема
Строчный ранг матрицы равен её столбцовому рангу.
Ранг матрицы
Определение
Рангом
матрицы![]() называется
ранг её системы строк или столбцов.
называется
ранг её системы строк или столбцов.
Обозначается ![]()
На практике для нахождения ранга матрицы используют следующее утверждение: ранг матрицы равен количеству ненулевых строк после приведения матрицы к ступенчатому виду.
Элементарные преобразования над строками (столбцами) матрицы не меняют её ранга.
Ранг ступенчатой матрицы равен количеству её ненулевых строк.
Пример
Задание.Найти
ранг матрицы
Решение.С
помощью элементарных преобразований
над ее строками приведем матрицу![]() к
ступенчатому виду. Для этого вначале
от третьей строки отнимем две вторых:
к
ступенчатому виду. Для этого вначале
от третьей строки отнимем две вторых:

От второй строки отнимаем четвертую строку, умноженную на 4; от третьей - две четвертых:

Ко второй строке прибавим пять первых, к третьей - три третьих:

Меняем местами первую и вторую строчки:

Далее четвертую и первую строки:

Ответ.![]()
Метод окаймления миноров
Теорема
Ранг матрицы равен наибольшему порядку отличного от нуля минору.
На
этой теореме базируется еще один метод
нахождения ранга матрицы - метод
окаймления миноров. Суть этого метода
заключается в нахождении миноров,
начиная с низших порядков и двигаясь к
более высоким. Если минор![]() -го
порядка не равен нулю, а все миноры
-го
порядка не равен нулю, а все миноры![]() -го
равны нулю, то ранг матрицы будет
равен
-го
равны нулю, то ранг матрицы будет
равен![]() .
.
Пример
Задание.Найти
ранг матрицы ,
используя метод окаймления миноров.
,
используя метод окаймления миноров.
Решение.Минорами
минимального порядка являются миноры
первого порядка, которые равны элементам
матрицы![]() .
Рассмотрим, например, минор
.
Рассмотрим, например, минор![]() .
расположенный в первой строке и первом
столбце. Окаймляем его с помощью второй
строки и второго столбца, получаем
минор
.
расположенный в первой строке и первом
столбце. Окаймляем его с помощью второй
строки и второго столбца, получаем
минор![]() ;
рассмотрим еще один минор второго
порядка, для этого минор
;
рассмотрим еще один минор второго
порядка, для этого минор![]() окаймляем
при помощи второй строки и третьего
столбца, тогда имеем минор
окаймляем
при помощи второй строки и третьего
столбца, тогда имеем минор![]() ,
то есть ранг матрицы не меньше двух.
Далее рассматриваем миноры третьего
порядка, которые окаймляют минор
,
то есть ранг матрицы не меньше двух.
Далее рассматриваем миноры третьего
порядка, которые окаймляют минор![]() .
Таких миноров два: комбинация третьей
строки со вторым столбцом или с четвертым
столбцом. Вычисляем эти миноры:
.
Таких миноров два: комбинация третьей
строки со вторым столбцом или с четвертым
столбцом. Вычисляем эти миноры:
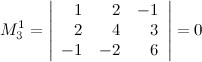
так как содержит два пропорциональных столбца (первый и второй); второй минор

преобразуем следующим образом: к первой строке прибавим третью, а ко второй две третьих:

И так как первая и вторая строки пропорциональны, то минор равен нулю.
Таким
образом, все окаймляющие миноры третьего
порядка равны нулю. А, значит, ранг
матрицы ![]() равен
двум:
равен
двум:![]()
Ответ.![]()
Теорема про визначник добутку матриць.
