Борман Теория разделения изотопов 2007

Иногда полезно использовать линейную аппроксимацию

c(1− c) ≈ a + bc ,

(1.314)

где a и b – константы. В этом случае уравнение (1.273) удается привести к следующей краевой задаче:

∂ς

2

− b

∂ς

;

= ∂

ς

∂t

∂y2

2 ∂y

2

a +bc

P

y

ς(y, 0) =

exp

−b

−1

ε b

a

+b c

0

2

2

a

+b

cP

ς(0,

τ) =

−1

ε

+b

c

b a

0

ς(y

0) = 0,

P,

где

ς =

(a +bc)L*

;

(a +bc0)P

cP

y

L* = 2P

a +b

exp

−b

−1 .

ε a +b

c

0

2

Решение краевой задачи (1.315) с учетом

a

+bc

P

y

P

= QPb

= exp

b

2

a +bc0

запишем в виде

a +b c

y

= exp

b

+

a +b c0

2

y

t

sin

πn y

∞

yP

+∑An exp b

−

,

y

n=1

4

t

b

n QP exp −b

2

−1

(1.315)

(1.316)

(1.317)

(1.318)

(1.319)

131

где

4b2QPb (ln qP)2

(−1)nQP −1,5b −1

An =

n

(1.320)

π 3

3b ln QP

2

b ln QP

2

+ n2

+ n2

2π

2π

1

ε

2

2πn

2

=

+

(1.321)

t

n

32ω b ln Q

P

Принимая y → yP = εSP , получим из выражения (1.321)

следующее соотношение для «положительного» конца идеального каскада

a +bcP(t)

∞

πn(−1)

n

t

= QPb

1

+ ∑AnqP−0,5b

exp

−

.

(1.322)

t

a +bc

n=1

b ln Q

0

P

n

Нетрудно

видеть,

что

рассмотренный

случай

c(1− c) ≈ a + bc

включает

в себя

также

линеаризацию при

c <<1 и 1− c <<1 (этим условиям будут соответствовать значения a = 0, b =1 и a = 1, b = −1). Соотношения (1.305),

(1.306), (1.313) и (1.322) можно использовать для расчета степени разделения (или концентрации в потоке отбора) идеального каскада в переходном режиме в произвольный момент времени.

Очевидно, что ряды в этих решениях будут сходящимися. Ограничиваясь случаем c <<1, исследуем сходимость выражения (1.305). Так как члены ряда в этом выражении знакопеременны, то согласно признаку Лейбница [26] погрешность при вычислении суммы ряда будет не больше первого из отброшенных членов. Значения отношения второго члена B2 к

первому B1 ряда (1.305) в момент времени t = t1 при различных значениях ln QP приведены в табл. 1.5.

132

Таблица 1.5

Значения отношений B2 /B1 в решении (1.305) при различных величинах ln QP

ln QP	0,5	1,0	1,5	2,0	2,5	3,0	3,5	4,0
B2 / B1	0,003	0,001	0,017	0,025	0,035	0,05	0,07	0,09

Из приведенных значений непосредственно следует, что вплоть до ln QP = 2 ÷2, 5 без существенной погрешности

можно ограничиться лишь первым членом разложения, и учитывая, что при t = 0, QP(0) =1, выражение (1.305) легко

преобразовать к виду

Q	P	(t)				t		,	(1.323)
			=1	−exp	−
Q						t
		P
						1

где t1 – так называемое время релаксации [7], определяемое

формулой (1.304) для n =1.

Если для рассматриваемого случая ввести в расчет степень приближения к равновесию ϕ , определяемую как отношение

	текущего обогащения к равновесному [7], то
	ϕ =	QP(t) −1	,	(1.324)
		QP −1

и время достижения заданной степени приближения к равновесию составит

t	= t	ln			1	.	(1.325)
ϕ	1		1		−ϕ

Из соотношения (1.325) следует, что время, необходимое для приближения к равновесию на 95–99 %, т.е. практическое время установления, будет равно (3 −5)t1 .

133

1.11.3. Переходный процесс в прямоугольном каскаде

[1, 3, 7, 35, 36]

Ограничимся рассмотрением случая, когда концентрации на ступенях каскада в течение всего переходного периода сохраняет малое значение, т.е. c <<1, концентрация у «отрицательного» конца каскада равна c = c0 и процесс осуществля-

ется при непрерывном и постоянном по величине потоке отбора. При сделанных предположениях основное уравнение (1.273) линеаризуется и принимает вид

∂c

=

∂2c

−(1+Ψ ) ∂c ,

(1.326)

∂τ

∂y2

∂y

гдеΨ =

2P

, которое должно удовлетворять условиям:

ε L

c(y, 0) = c0

(0 < y < yP),

(1.327)

c(0,τ) = c0

(τ > 0),

(1.328)

∂c

−c

y=y = 0.

(1.329)

∂y

y=y

P

P

Решение (1.326) удобнее выполнить, вводя новую зависимую переменную следующим образом

u = c − c0 ,

тогда (1.326) – (1.329) перепишутся в виде

	∂u	=	∂2u	−(1+Ψ )	∂u	,
	∂τ		∂y2		∂y

u(y, 0) = 0 (0 < y < yP),

	u(0,τ) = 0					(τ > 0),
	∂u		−u		y=y	= c0.
	∂y	y=y
			P			P

(1.330)

(1.331)

(1.332)

(1.333)

(1.334)

134

Решая уравнение (1.331) методом интегральных преобразований Лапласа , получим в изображениях

+Ψ

1+Ψ

2

1

u = A exp

+

+ p y +

2

2

(1.335)

2

1+Ψ

+B exp

1+Ψ

−

+ p y .

2

2

Из условия (1.333) найдем B = −A и

= 2A exp 1

(1+Ψ )

y

1

+Ψ

2

u

sh

+ p

y .

(1.336)

2

2

A , под-

Используя условие (1.334), определим значение

ставив которое в (1.336), получим

u

= c

exp −

1 (1+ψ )(y

P

− y ) ×

0

2

1+Ψ

2

+ p

sh

1+Ψ

2

×

×

2

2

+ p y

(1.337)

1+Ψ

2

1

+Ψ

2

×

+ p ch

+ p ×

2

2

1−ψ

1+Ψ

2

1

+Ψ

2

−1

×yP −

+ p sh

yP .

2

2

2

Пользуясь теоремой разложения и переходя к оригиналу, получим, что изменение концентрации у «положительного» конца ПК составит

Правила операционного исчисления коротко изложены в приложении 2.

135

1+Ψ

y

cP (τ)

1+ th

2

P

=

+

c0

1

−

1

−Ψ

1+Ψ

y

1

+Ψ

th

2

P

(1.338)

(1

+Ψ )2 y

2

− 4r 2

r 2 exp

−

4

P

n

τ

n

y 2

+

32y

P

∑

P

,

(1

+Ψ )2

y

2

−

4r

2 (1−Ψ )

2 y2

−

2y

− 4r 2

n

P

P

n

P

n

где rn корни характеристического уравнения

th rn =

2rn

.

(1.339)

(1

−Ψ ) yP

Значения этих корней приведены в приложении 3.

Если в течение переходного процесса отбор выключен, то Ψ ≡ 0 и (1.339) приводится к виду [37]:

y 2

−

4r

2

r 2 exp −

P

n

c

(τ)

4

P

n

y 2

= exp( yP ) + 32 yP ∑

P

. (1.340)

c

y

2

− 4r

2

y

2

− 2y

−

4r

2

0

n

P

P

P

n

n

Из сравнения (1.339) и (1.340) следует, что при наличии отбора достижение заданной концентрации у «положительного» конца ПК требует большего времени, чем в случае работы ПК в безотборном режиме.

В случае yP → ∞ соотношение (1.337) может быть упрощено, и для «положительного» конца ПК (y = yP) получим

												c0
			u =																=
							1		+Ψ 2						1	−Ψ
									2			+ p −
																	2			(1.341)
															1		+Ψ 2
													p
c				1+Ψ						2									+ p
		0															2
=											+ p	−								.
																p +Ψ
Ψ				2

136

Переходя к оригиналам, с учетом (1.330) имеем

cP(τ)

=1+

1 1

+Ψ erf

1

+Ψ

τ

+1

−Ψ 1−exp (−ψτ) ×

c0

Ψ

2

2

2

(1.342)

1−Ψ

1

−ψ

1

−Ψ

+erf

τ

−

erf

τ

× 1

.

2

2

2

2

z

где

erf z =

∫exp(−x2 )dx .

(1.343)

π

0

При Ψ → 0

в

формуле

(1.342)

возникает неопределен-

ность, раскрывая которую найдем отношение концентраций в безотборном режиме, когда c <<1

c

P

(τ)

=

+

τ

+erf

τ

+

τ

−

τ

. (1.344)

1

1

exp

c

2

2

π

4

0

Численный анализ показывает, что при одинаковых безразмерных временах τ значения концентрации в потоке отбора, получаемые с помощью формулы (1.341), всегда превышают значения, получаемые с помощью формулы (1.340).

Сравним теперь переходные процессы, протекающие в идеальном и прямоугольном каскадах.

На рис. 1.29 приведено отношение времен при одинаковом значении коэффициента ϕ = 0,95 идеального каскада t* и прямоугольного каскада tПК в зависимости от степени разделения QP = RP R0 для случая c <<1. Время tПК рассчитываем по формуле (1.338), а t * – по формуле (1.325).

Следует отметить, что величины t*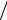tПК в широком диапазоне QP практически совпадают с соответствующими величинами КПД формы прямоугольного каскада. Качественно это можно объяснить тем, что времена t* и tПК пропорциональны накоплению изотопа, а накопление, в свою очередь,

137

пропорционально объему каскада и соответственно для ПК определяется КПД формы.

Рис. 1.29. Зависимость величины t* / tпк от степени разделения Qp = Rp /R0 для случая малых концентраций ( c << 1) [33]

3. Оценка времени установления по отношению суммарного накопления ценного изотопа в каскаде к средней скорости его накопления [4]

Рассмотрим упрощенный подход для оценки времени выхода каскада на стационарный режим работы.

Исходные предположения:

1)в начальный момент времени каскад заполнен смесью с концентрацией ценного изотопа cF ;

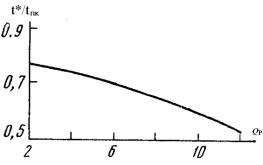
2)так как время выхода каскада на стационарный режим работы tP определяется в основном обогатительной частью,

рассмотрим случай yW = 0 (отсутствие обеднительной части). На «отрицательном» конце каскада (s = 0) поддерживают постоянное значение концентрации c (0,τ) = c0 . Это эквива-

лентно тому, что к «отрицательному» концу каскада подсоединен резервуар бесконечного объема, содержащий рабочее вещество с концентрацией c0 (см. рис. 1.30).

138

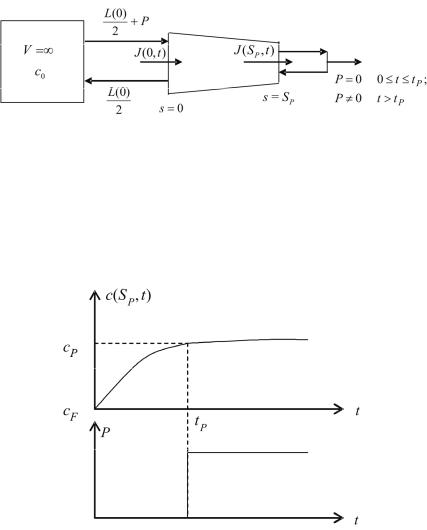
Рис. 1.30. Схема каскада в бесконечном резервуаре на «отрицательном» конце

3) в период времени [0,tP ] поток отбора выключен. Он включается в момент времени t = tP , когда концентрация на

«положительном» конце достигает расчетного значения cP

(рис. 1.31).

tP

Рис. 1.31. Качественные зависимости, поясняющие момент включения потока отбора из каскада

Для того, чтобы вывести каскад на стационарный режим работы, в нем следует накопить ценный изотоп (полное накопление) в количестве

139

	SP
M%	=ω ∫ L(s)[c(s) −cF ]ds .	(1.345)
	0
Обозначим через	J (0,t) и J(SP, t) соответственно поток

ценного изотопа через начальную и конечную ступени в момент времени t . Поток изотопа через произвольную ступень s в момент времени t равен:

		L(s)				∂c(s,t)
	J (s,t) =		εc(s,t)[1	− c(s,t)(1	− c(s,t))]−	∂t		. (1.346)
		2

Тогда скорость накопления ценного изотопа в каскаде для 0 ≤ t < tP будет равна

∆J(t) = J(0, t) − J(SP, t) =

=

ε

L(0) c(0, t) (1−c(0, t))− L(S

P

) c(S

P

(

−c(S

P

)

+

, t) 1

, t

2

+

1

)

∂c

− L(0)

∂c

(1.347)

2

L(S

P

∂s

∂s

.

s=S

s=0

P

Величины (1.345) и (1.347) связаны очевидным соотношением

tP
%			(1.348)
M = ∫∆J (t)dt .
0
Интеграл в (1.348) можно представить в виде
tP
∫∆J (t)dt =	∆J	tP ,	(1.349)
0

где ∆J – средняя скорость накопления ценного изотопа за временной промежуток [0, tP] , тогда время tP можно оце-

нить по формуле

tP =	M		.	(1.350)
	∆J

140