Борман Теория разделения изотопов 2007

g

+

m

ε

c

k

1

∑

jk

j

θ =

j=1

,

(2.26)

1 + gk

gk qik

ϕ

i

=

,

i =1, 2,..., m .

(2.27)

1

+ gk

Если коэффициенты разделения αik , βik

не зависят от кон-

центрации, то в соответствии с (2.27) парциальные срезы не будут зависеть от концентрации. Однако при этом согласно формуле (2.26) срез θ должен зависеть от концентрации. Из этой формулы следует, что если срез θ не зависит от концентрации, то gk , αik и βik должны зависеть от концентрации.

Назовем симметричной относительно пары компонентов с номерами n и k ступень (элемент), в которой коэффициенты разделения этой пары αnk и βnk одинаковы: αnk = βnk =

= qnk , так что в соответствии с (2.20) параметр gk равен

g		k		=	1	=	1 .	(2.28)
					βnk		qnk
Остальные коэффициенты (i ≠ k) , срез θ								и срезы парци-
альных потоков ϕi в такой ступени (элементе) имеют вид:
α	ik			= qik (1 +			qnk ),	(2.29)
					qik	+	qnk
β			ik	= qik		+	qnk ,	(2.30)
					1 + qnk
					m
					1+ ∑ε jk c j
θ =					j=1		,	(2.31)
					1+	q
							nk

181

	ϕi	=	αik		, i = 1, 2,..., m .	(2.32)
			+	qnk
		1

При «слабом» обогащении на ступени (элементе), когда коэффициенты разделения qik , αik и βik мало отличаются от

единицы, можно считать

ε

ik

≈ ln q

,

ε′

≈ lnα

ik

,

ε′′

≈ ln β

ik

,

(2.33)

ik

ik

ik

и, следовательно, в соответствии с (2.33) и (2.13)

ε

ij

= −ε

ji

,

ε

′

= −ε′ ,

ε′′ = −ε′′

,

(2.34)

ij

ji

ij

ji

ε

ij

= ε

ik

+ ε

kj

,

ε

′

= ε′

+ ε′

,

ε′′

= ε′′

+

ε

′′

,

(2.35)

ij

ik

kj

ij

ik

kj

ε

ik

= ε′

+ ε

′′

.

(2.36)

ik

ik

Из (2.34) – (2.36) следует, что в случае «слабого» обогащения относительные коэффициенты обогащения обладают свойствами антисимметричности и аддитивности. Кроме того, можно считать, что для однофазных методов разделения выполняется соотношение εik = ε0(M K − M i ) , где ε0 – коэф-

фициент обогащения при единичной разности массовых чисел, M k и M i массовые числа k-го и i-го компонентов соот-

ветственно [3, 4].

В этом случае согласно (2.26)

θ

=

gk

(2.37)

1 + gk

g

=

εik′′

θ

и, соответственно,

k

=

.

(2.38)

ε

′

1 −θ

ik

Тогда с учетом (2.36) и (2.38) коэффициенты εik′

и εik′′ мо-

гут быть записаны в виде

ε′

= (1 −θ)ε

ik

,

ε′′

=θε

ik

.

(2.39)

ik

ik

С учетом (2.1) и (2.35) соотношения (2.22) в рассматриваемом случае преобразуются следующим образом:

182

m

m

m

δi′ = ci εik′ −

∑ε

′jkc j

= ci

∑εik′ c j − ∑ε jk c j

=

j=1

j=1

j=1

= c

m

(ε′

c

−

ε′

c

= c

m

(ε

′

−

ε′

)c

=

(2.40)

∑

j

j

)

j

i

ik

jk

i

∑

ik

jk

j=1

j=1

= c

m

(ε′

+ε

′

= c

m

ε′c

.

∑

)

∑

j

i

ik

kj

i

ij

j=1

j=1

Аналогично получаем:

m

δi′′= ci ∑εij′′c j ,

(2.41)

j=1

m

δi

= ci ∑εijc j.

(2.42)

j=1

2.2.Основные уравнения противоточного симметричного разделительного каскада

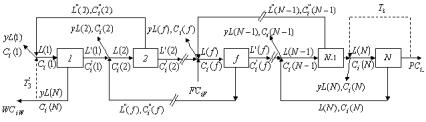
Рассмотрим противоточный симметричный каскад с одним входящим потоком питания F и двумя выходящими – отбора P, обогащенного самым легким компонентом и отвала W, обогащенного самым тяжелым компонентом (рис. 2.2). Пото-

ки F, P, W и их концентрации ciF , ciP, сiW (i =1, 2,..., m) являются внешними параметрами каскада.

Рис. 2.2. Схема противоточного разделительного каскада

183

Если потери вещества в ступенях каскада отсутствуют, то внешние параметры каскада должны удовлетворять уравне-

ниям материального баланса
F = P +W,
	(2.43)
Fci,F = Pci,P +Wci,W , i =1, 2,..., m.

Ступени каскада пронумерованы последовательно от s = 1

на отвальном конце каскада до s = N на отборном			конце
каскада; считаем, что поток питания F подают на вход ступе-
ни	с номером f. Внутренние параметры	каждой	ступени
Ls,	L′s, L′′s, Gi,s = Lsci,s, G′s = L′sc′i,s, G′′s = c′′i,s	в стационарном

состоянии каскада связаны уравнениями баланса вещества и каждого компонента

	Ls = L′s + L′′s,	s =1,..., N ;	(2.44)
	Gi,s = Gi′,s +Gi′′,s или
′ ′	′′ ′′	2,..., N i =1, 2,..., m,	(2.45)
Lsci,s = Lsci,s	+ Lsci,s, s =1,

где индекс i означает номер компонента, а индекс s – номер ступени.

Уравнения коммутации потоков при симметричном соединении ступеней имеют вид:

	Ls = L′s−1 + L′′s+1 или
	Ls =θs−1Ls−1 +(1−θs+1)Ls+1,	s =1, 2,..., f −1,	f +1,..., N,	(2.46)
	Gi,s = Gi′,s−1 +Gi′′,s+1 или
	Lsci,s =θs−1Ls−1c′i,s−1 +(1−θs+1)Ls+1c′′i,s+1,			(2.47)
	s =1, 2,..., f −1,	f +1,..., N, i =1,	2,..., m.
	Для ступени питания	s = f уравнения коммутации пото-
	ков можно записать как
	L f = L′f −1 + L′′f +1 + F или
	Lf =θ f −1Lf −1 + (1 −θ f +1)Lf +1 + F,			(2.48)

184

Gi, f	= Gi′, f −1 +Gi′′, f +1 + Fci,F					или
Li, f = θf −1Ls −1ci′, f −1			+ (1 −θf +1 )Lf +1ci′′, f +1,			i = 1, 2,..., m . (2.49)
Концентрации	c	,	c′	, c′′	на каждой ступени связаны
	i,s		i,s	i,s

соотношениями (2.14) – (2.15). Внешние и внутренние параметры каскада связаны граничными условиями

′	′′			′	′′	= 0,	(2.50)
L0 = L0 = L0 = LN +1 = LN +1 = LN +1
	L′N =θN LN = P ,						(2.51)
	L1′′= (1−θ1)L1 =W ,						(2.52)
c′N = ciP,		i =1,		2,..., m,			(2.53)
c1′′= ciW ,		i =1, 2,..., m,					(2.54)
Gi′,N	= PciP,		i =1,		2,..., m,		(2.55)
Gi′′,1	=WciW ,		i =1,		2,..., m .		(2.56)

Соотношения (2.43) – (2.56) представляют простейшую математическую модель противоточного симметричного каскада, предназначенного для разделения многокомпонентной смеси. При решении некоторых разделительных задач вместо уравнений (2.46) – (2.47) удобнее пользоваться разностными уравнениями, отражающими баланс потоков в сечениях между ступенями:

для отборной части каскада

			L′	− L′′			= P или
			s		s+1
		θs Ls − (1 −θs+1)Ls+1 = P,								(2.57)
	L c′	Gi′,s −Gi′′,s+1					= Pci,P или
θ		− (1 −θ	s+1	)L	c′′			= Pc	i =1, 2,..., m ,	(2.58)
	s s i,s			s+1		i,s+1		i,P
для отвальной части каскада
		L′ − L′′				= −W или
			s	s	+1
		θs Ls − (1 −θs+1)Ls+1 = −W ,								(2.59)

185

Gi′,s −Gi′′,s+1 = −WciW или

θsLsc′i,s −(1−θs+1)Ls+1c′′i,s+1 = −WciW i =1, 2,..., m , (2.60)

В свою очередь, система (2.57) – (2.58) может быть легко преобразована к виду

ci,s+1 −ci,s =

θsLs

δi′,s +δi′′,s+1 −

P(ciP −ci,s)

, (2.61)

(1−

θ

)L

(1−θ

s+1

)L

s+1

s+1

s+1

i =1,

2,..., m;

s = f ,..., N,

где δ′

= c′

− c

–

функция,

определяемая соотношением

i,s

i,s

i,s

(2.22) и представляющая изменение концентрации i-го компонента на s-й ступени, а δi′,s и δi′′,s связаны уравнением ба-

ланса δi′′,s = 1−θθ δi′,s .

Соответственно, система (2.59) – (2.60) может быть представлена в виде

ci,s+1 −ci,s =	θsLs				δi′,s +δi′′,s+1 −	W (ci,s −ciP)			, (2.62)
	(1−θ	s+1	)L	s+1		(1−θ	s+1	)L
								s+1
i = 1, 2,..., m;					s = 1, 2,..., f −1.

Нетрудно видеть, что системы (2.46) – (2.49), (2.57) – (2.60)

и (2.61) – (2.62) эквивалентны. Каждая из них представляет систему нелинейных разностных уравнений относительно функций ci,s . Более того, в эти уравнения (или в их гранич-

ные условия) входят значения концентраций, которые должны определяться из решения этих же уравнений. Аналитическое решение подобных систем возможно лишь в отдельных частных случаях. При произвольном распределении Ls воз-

можно лишь численное решение этих систем на ЭВМ. Вопрос о расчете каскада с использованием систем (2.46) –

(2.49), (2.57) – (2.60) и (2.61) – (2.62) включает две задачи:

–расчет каскада заданного профиля (поверочный расчет);

–проектировочный расчет каскада.

186

Под расчетом каскада заданного профиля, как правило, прямоугольного или прямоугольно-секционированного, подразумевают: при заданных числах ступеней и потоков в секциях, потоке питания F с концентрациями компонентов

ciF	(i =1, 2,..., m) , одного из выходящих из каскада пото-
ков – P или		W,	относительных		коэффициентов разделения
qik , αik , βik		определение концентраций компонентов в пото-
ках	отбора	ciP	(i =1,	2,..., m) ,	отвала	ciW	(i =1, 2,..., m) ,
распределение			среза	θs и	концентраций		компонентов
ci,s (i =1, 2,..., m)			по ступеням		каскада.	Такой поверочный

расчет необходим при исследовании оптимального управления процессом разделения, при изменении режимов работы и отдельных параметров разделительного каскада, а также при многоцелевом использовании каскада, например, для разделения изотопов различных элементов. Основные трудности поверочного расчета связаны с тем, что неизвестные концентрации ciP и ciW (i =1, 2,..., m) входят в основные уравне-

ния. Невозможность аналитического решения этих уравнений вызывает необходимость разработки численных методов, ма-

лочувствительных к заданию начальных приближений ciP и ciW (i =1, 2,..., m) . Под проектировочным расчетом обычно

понимают определение параметров прямоугольного или пря- моугольно-секционированного каскада по заданным значениям концентрации одного из компонентов (целевого или ключевого) в потоках отбора и отвала и величине потока отбора. При этом подразумевается, что искомые параметры каскада должны наилучшим образом удовлетворять условиям его оптимальности.

187

2.3. Каскад в случае слабого разделения

2.3.1. Основные уравнения [2–4]

Важное практическое значение имеют каскады, состоящие из разделительных ступеней (элементов) слабого обогащения, когда полные относительные коэффициенты обогащения

εik = (εik′ +εik′′ ) <<1. При тех же предположениях, что и в би-

нарном случае ( N >>1, θ ≈

1

и т.д.), переходя от разностных

2

уравнений (2.61), (2.62) с учетом (2.39) – (2.42), получаем

dci

m

2P

= ci ∑εijc j

−

(ciP −ci),

(2.63)

ds

L(s)

j=1

m

0 ≤ s ≤ S p (SP +1 = N − f ),

i =1,

2,..., m −1,

∑c j =1;

j=1

dci

m

2W

= ci ∑εijc j

−

(ciW −ci),

(2.64)

L(s)

ds

j=1

m

0 ≤ s ≤ SW (SW = f ),

i =1, 2,..., m −1, ∑c j =1,

j=1

где SP и SW – числа ступеней в отборной и отвальной частях

каскада, s – текущий номер ступени в отборной и отвальной частях каскада. Нумерация ступеней в обеднительной части ведется от концевой ступени к ступени, на вход которой подают поток питания, а в обогатительной части – от ступени ввода питания к отборному концу каскада.

Анализ (2.63), (2.64) позволяет сделать следующие замечания о свойствах уравнений каскада.

1. В случае безотборного режима ( P =W = F = 0 ) система (2.63), (2.64) легко интегрируется, и ее решение имеет вид:

188

ci (s) =	ci	(0)	,	(2.65)
	m
	∑c j (0) exp(−εijs)

j=1

где ci (0) – концентрация i-го компонента на входе в ступень,

номер которой s = 0 принят за начало отсчета. Из соотношения (2.65) видно, что распределения концентраций по ступеням каскада в безотборном режиме не зависят от распределения потока L(s) . Анализ (2.65) показывает также, что если

каскад достаточно длинный, то концентрации всех промежуточных компонентов имеют максимум внутри каскада и только концентрации крайних компонентов непрерывно возрастают к концам каскада. Явление локализации компонентов в разных местах каскада имеет простое физическое объяснение. Разделительный каскад можно описать при помощи силового поля постоянной напряженности. В результате конкуренции в этом поле наиболее активные компоненты вытесняют менее активные с концов каскада, а те, в свою очередь, аналогичным образом действуют на еще менее активные.

2. Из анализа системы (2.63) – (2.64) (а также систем

(2.46) – (2.49), (2.57) – (2.60), (2.61) – (2.62)) непосредственно следует, что невозможно построить многокомпонентный каскад, в котором выполнялись бы условия несмешения на входах в ступени одновременно по всем концентрациям. Это связано с тем, что перенос всех компонентов в каскаде описывается системой m-уравнений, а параметр, с помощью которого можно обеспечить условие несмешения, всего один – L(s).

3. В связи с тем, что при любом числе компонентов обогащение в ступени самого легкого компонента смеси

m

δ1 = c1∑ε1 jc j всегда строго положительно, а самого тяжело-

j=1

189

m

го δm = cm ∑εmjc j , наоборот, всегда меньше нуля, выделе-

j=1

ние их не представляет проблемы. В отличие от этого знаки обогащения промежуточных компонентов зависят от состава смеси. Поэтому на некотором удалении от точки питания их концентрации перестают возрастать, т.е. в каскаде удается добиться лишь ограниченного обогащения промежуточных компонентов в отборе.

Задача выделения промежуточного компонента сводится, очевидно, к выбору такого профиля L(s) , при котором кон-

центрация ключевого (целевого) компонента в потоке отбора (или отвала) имеет максимальное значение. В работе [5] показано, что в каскаде с одним потоком отбора и одним потоком отвала предельную концентрацию произвольного n-го компонента в потоке отбора можно оценить по формуле

cмакс =	cnF	.	(2.66)
nP	n
	∑c jF

j=1

На практике часто требуется получить концентрацию промежуточного компонента по величине большую, чем дает формула (2.66), для чего целесообразно либо включение дополнительного отбора в месте локализации ключевого (целевого) компонента, либо использование более сложных каскадных схем (двойной каскад и др.).

2.3.2.Исследование каскадов заданного профиля методом ортогональной коллокации (МОК) [6]

Как было указано выше, сложность расчета каскада заданного профиля обусловлена, во-первых, нелинейностью уравнений каскада (2.63), (2.64), во-вторых, трудностью определения начальных приближений для концентраций на концах каскада, которые, являясь граничными условиями уравнений каскада, сами явно входят в эти уравнения.

190