Борман Теория разделения изотопов 2007

Оценим теперь среднюю скорость накопления в начальный момент времени ∆J(0) = J(0, 0) − J(SP, 0) и в момент времени

t = tP , ∆J(tP) = J(0, tP) − J(SP, tP) .

При t = 0 ,

c(0, 0) = c

0

,

∂c

= 0;

∂s

s

=0

t =0

c(S

P

, 0)

= c

P

,

∂c

= 0 .

∂s

s=0

Следовательно,

1 εc

t =0

(0) =

(1−c

)

L(0)

− L(S

)

.

(1.351)

∆J

2

0

0

P

Для любого момента времени t′

t

′

′

> tP , c(0, t ) = c0

∂c

=

εc

(1−c

) −

2P

(c

P

−c

) ,

∂s

s=0

0

0

L(0)

0

∂c

c(sP , t′) = cP ,

= εcP(1−cP) ,

∂s

s=S

′

P

′

при этом J (0, t ) = PcP ,

и,

следовательно,

J(SP, t ) = PcP,

∆J (t′) = 0 .

При t = tP поток отбора скачком меняет свое значение от нуля до расчетного значения (рис. 1.31). Будем считать, что

при этом функции c(0,t) ,

c(S

P

, t) и

∂c

остаются непре-

∂s

s=S

P

рывными. В этом случае можно написать при t = tP :

P = 0 , c(0, t

P

) = c

∂c

= εc

(1−c

) −

2P

(c

P

−c

) ,

0

∂s

s=0

0

0

L(0)

0

141

c(SP, tP) = cP

∂c

= εcP(1−cP) ,

∂s

s=S

и, следовательно,

P

∆J(tP) = P(cP −c0) .

(1.352)

Предполагая, что функция ∆J (t) монотонная, аппрокси-

мируем среднее значение

∆J

формулой

(1.353)

∆J

= (1− K ) ∆J (0) + K ∆J (tP ) ,

где 0 ≤ K ≤1.

Оценим

теперь

tP

для

идеального

каскада. Поскольку

*

4P(cP −c0)

*

*

L (0) =

и

L (SP) = 0 ,

и, следовательно

∆J

(0) =

εc0(1−c0)

= 2P(c

P

−c

) ,

∆J

*(l

P

) = P(c

P

−c

) ,

то в соответствии с фор-

0

0

мулой (1.353)

= (2 − K) P(cP −c0) .

(1.354)

∆J *

Ограничиваясь случаем c <<1, определим полное накоп-

ление M *

SP

*

cP

*

−c0 )

%

∫

∫

L (c)(c

Mп =ω

L (s)(c −c0 )ds

=

ω

dc

*

dc =

0

cF

ds

cP 4P(c

−c)(c−c )

8ωP cP c c−c c

−c2

+c c

=ω ∫

P

0

dc =

2

∫

P

P

0

0

dc =

(1.355)

1

ε

c2

ε

c

2

cF

cF

2

=8εω2P (cP +c0 )ln cP −2(cP −c0 ) .

c0

Подставляя (1.354), (1.355) в (1.350), получим

142

t*

=

1

8 ω

E(c

, c

) ,

2

− K

ε 2

P

P

0

(c

P

+c

) ln

cP

где

E(c

, c

) =

0

c0

−2 .

P

0

cP −c0

Так как 0 ≤ K ≤1, то

8ω E(c

1 8ω E(c

, c

) ≤ t*

≤

, c

) .

2 ε 2

P

0

P

ε 2

P

0

Если

ε = 3×10−3, ω = 30c, c

P

= 3,5%, c

F

= 0, 7%

8ω

E(c

, c

)

≈127 дней.

P

F

ε 2

(1.356)

(1.357)

(1.358) [4], то

Вслучае, если каскад прямоугольный, то L(0) = L(SP) ≡ L,

∆J(0) = 0, ∆J(tP) = P(cP −c0) и, следовательно,

∆J

= K P(cP −c0) .

(1.359)

Оценим накопление в ПК следующим образом. Пусть c – средняя по длине каскада концентрация ценного изотопа в

ПК, работающем в стационарном режиме.
Если положить
′	′	′	0 ≤ K	′	≤1,	(1.360)
c = K cP +(1− K )c0		= c0 + K (cP −c0),
то полное накопление с учетом (1.360) можно оценить как
SP
M% п =ω ∫	L(cP −c)ds =ωLK '(cP −c0)SP ,					(1.361)
0

подставляя (1.361) и (1.3360) в (1.350), получим

tP = εω2 KK′ εPL εSP . (1.362)

В работе [4] по выбору величины K′ даны следующие ре-

комендации:				0 ≤ K′ ≤ 0,5;
для	c	P	< 50%,
				0,5 ≤ K′ ≤1;
для	c0		≥ 50%,		(1.363)
для	c0 < 50% < сP, K′ ≈ 0,5 .

143

	−3	′		εL
	При ε = 3×10 , ω = 30 c, K		= 0, 25, K =1,
				P =10, 70 и

εSP = 2, 48, tP = 275 дней, что менее, чем на 10%, отличается

от соответствующей величины, полученной из решения задачи численным методом.

1.12. Несимметричные каскады [3, 40–46]

В разделе 1.7 на примере симметричного идеального каскада показано, что соединение несимметричных ступеней (α ≠ β) в такой каскад не может обеспечить для каждой из

них режим работы, близкий к оптимальному. В результате суммарный поток в каскаде оказывается больше минимально возможного. Для таких способов разделения смесей, как сопло Беккера [38] или разделение на полупроницаемых мембранах [39], применение несимметричных ступеней с существенным отличием величины θ от 0,5 является принципиальным. Так, согласно [38], при разделении изотопов урана в виде UF6 оптимальный режим работы сопла Беккера осуществляется при θ = 0,2.

Как известно, изменить значение коэффициента деления потока на ступенях каскада можно за счет изменения схемы их соединения, применяя, например, несимметричные схемы противоточных каскадов, в которых обогащенный поток θsLs

с s-й ступени подается на вход (s + k)-й ступени, а обедненный поток (1 – θsLs ) возвращается на вход (s – p + 1)-й сту-

пени, причем k ≥1, p ≥ 2 . В частном случае k =1,	p = 2
каскад будет работать в симметричном режиме.
Как будет показано ниже, изменением величин k	и p

можно достичь как меньших, так и больших по сравнению с симметричным каскадом значений θs .

Ниже приводятся основные сведения из теории несимметричных каскадов, разработанной авторами работ [3, 40–46].

144

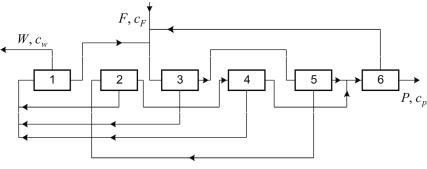
1.12.1.Основные уравнения несимметричного каскада. Идеальный несимметричный каскад с произвольным обогащением на ступени

Несимметричный каскад имеет, вообще говоря, k отборов и p −1 отвалов. При малом обогащении на одной ступени

можно считать концентрации всех отборов и соответственно всех отвалов приближенно одинаковыми. Это предположение значительно упрощает условия на концах каскада.

Для каскадов с большими обогащениями на ступенях такое предположение неправомочно и необходимо уточнить условия соединения ступеней на концах каскада. Можно принять, что на отборном конце каскада все обогащенные потоки со ступеней N −k ≤ s ≤ N подаются на вход последней N-й ступени, а на отвальном конце все обедненные потоки со ступеней 1 < s ≤ p подаются на вход первой ступени. Схема тако-

го каскада в частном случае k = 2, p = 4, N = 6 показана на рис. 1.32.

Рис.1.32. Несимметричный каскад из шести ступеней

Баланс полных потоков и потоков обогащенного компонента на входе в некоторую ступень, где 1+ k ≤ s ≤ N −( p −1) дает

Ls−kθs−k + Ls+( p−1) (1 −θs+( p−1) ) = Ls ,

(1.364)

145

	L	θ	s−k	(c	s−k	+δ′	−k	)	+
	s−k					s				(1.365)
	+ Ls+( p−1) (1−θs+( p−1) )(cs+( p−1) +δs′′+( p−1) = Lscs .

Если на одну из ступеней с номером s = f подается поток питания F с концентрацией cF , то для этой ступени можно

написать
F + Lf −kθ f −k + Lf +( p −1) (1 −θ f +( p −1) ) = Lf ,	(1.366)

	FcF	+ Lf −kθf −k (c f −k	+δ′f	−k ) +	(1.367)
	+ Lf +( p−1) (1−θ f +( p−1) )(c f +( p−1) +δ′′f +( p−1) = Lf c f .

На отборном конце каскада те же уравнения принимают

более простой вид:

Ls−kθs−k

= Ls ,

N −( p −1) < s < N ;

(1.368)

′

−( p −1) < s < N,

(1.369)

Ls−kθs−k (cs−k +δs−k ) = Lscs, N

k

∑LN −iθN −i = LN ,

(1.370)

i=1

k

∑LN −iθN −i(cN −i +δ′N −i) = LNcN ,

(1.371)

i=1

LNθN = P,

(1.372)

LNθN (cN +δ′N ) = Pcp ;

(1.373)

и, соответственно, для отвального конца

Ls+( p−1) (1−θs+( p−1) ) = Ls ,

1 < s <1 + k ;

(1.374)

L

(1−θ

s+( p−1)

)(c

s+( p−1)

−δ′′

)

= L c

,

;

(1.375)

s+( p−1)

s+( p−1)

s s

1 < s < 1+ k

p−1

∑Li+1(1−θi+1) = L1 ;

(1.376)

i=1

p−1

∑Li+1(1−θi+1)(ci+1 −δi′′+1) = L1c1 ;

(1.377)

i=1

146

	L1(1−θ1) = W ;			(1.378)
L (1−θ )(c −δ′′) = Wc		w	.	(1.379)
1	1 1 1

Если приращение концентрации (функцию обогащения) на

произвольной s-й ступени задать в виде
c′	− c	s	= δ′ = f (c				,θ	s	) ,	(1.380)
s				s		s
причем, согласно балансу потоков
	δs′ =			1−θs	δs′′,					(1.381)
				θs

то система уравнений (1.364) – (1.379) представляет полную систему для любого каскада с заданным профилем. При этом подразумевается, что отбор P, концентрации в потоках отбора cp и отвала cw заданы, а значения Ls должны оставаться в

известных пределах, чтобы не получилось отрицательных обогащений. Кроме того, следует учитывать, что обогащение на одной ступени конечно и при строгом выполнении условий баланса число ступеней может оказаться «дробным». При необходимости точной корректировки считают, что одна из величин Ls не является произвольной.

Для построения идеального несимметричного каскада необходимо использовать условие отсутствия смешивания кон-

центраций на входах в разделительную ступень
cs′−k = cs = cs′′+( p−1) .	(1.382)

Условие (1.382) дает возможность из уравнений (1.365), (1.369), (1.370), (1.374), (1.376) после алгебраических преоб-

разований и с использованием условия (1.380) и граничных условий (1.373) и (1.379) получить соотношения для приращения концентраций на разделительной ступени несимметричного идеального каскада

cs −cs−k = f (cs−k ,θs−k ), 1+ k ≤ s < N ,	(1.383)
cN −cs−k = f (cs−k ,θs−k ), N ≤ s < N + k ,	(1.384)

147

cp −cN = f (cN ,θN ) .

(1.385)

и формулы для определения коэффициентов деления потоков

θs =	cs −cs−( p−1)	, 1+( p −1) < s < N −k ,	(1.386)
	cs+k −cs−( p−1)

θs = cs −cs−( p−1) , N −k ≤ s < N ;

cn −cs−( p−1)

θs = cs −−c1 , 1 < s ≤ 1+ ( p −1) ; cs+k c1

	θ		=		c1 − cw		,
	1				c1+k − cw
	θN	=		cN		−cN −( p−1)		.
				cp		−cN −( p−1)

(1.387)

(1.388)

(1.389)

(1.390)

Для получения полной системы уравнений несимметричного идеального каскада достаточно к уравнениям (1.383) – (1.390) добавить уравнения баланса по полным потокам или по потоку ценного (целевого) компонента на выбор. Рассматривая первый случай, можно утверждать, что системы уравнений (1.383)–(1.385), (1.386)–(1.390) и уравнения (1.364), (1.366), (1.368), (1.370), (1.372), (1.374), (1.376), (1.378) образуют полную систему уравнений идеального несимметричного каскада при произвольных обогащениях на отдельной ступени.

Для случая, когда полный коэффициент разделения не зависит от θ , для идеального несимметричного каскада может быть получено аналитическое решение.

В качестве примера рассмотрим такой тип каскада, в котором ступени соединены так, что обогащенная фракция со ступени s направляется на питание ступени s + 2, а обедненная фракция подается на вход (s-1)-й ступени, т.е. k = 2, p = 2.

148

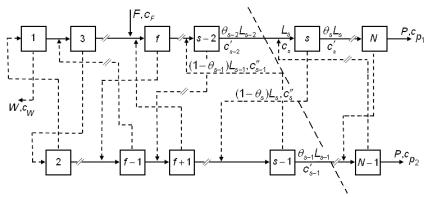
Такой каскад дает два потока отбора P1 и P2 с концентрациями cP1 и cP2 и один поток отвала с концентрацией cW

(рис. 1.33).

Рис. 1.33. Схема несимметричного каскада с обогащенным потоком, выходящим из произвольной ступени, подаваемым через одну ступень «вперед» в прямом направлении и обедненным потоком, подаваемым на вход предыдущей ступени

Уравнения материального баланса для обеднительной части каскада, находящейся между точкой отвала и произвольной ступенью s, имеют вид

θsLs +θs−1Ls−1 +W = (1−θs+1)Ls+1 ,	(1.391)
θsLsc′s +θs−1Ls−1c′s−1 +W = (1−θs+1)Ls+1c′′s+1 .	(1.392)

Аналогичные соотношения для обогатительной части каскада можно записать следующим образом

θsLs +θs−1Ls−1 = P1 + P2 +(1−θs+1)Ls+1 ,

(1.393)

θ

′

+θ

′

= Pc

+ P c

+(1−

θ

)L

′′

. (1.394)

L c

s

L c

P 2

s

c

s s

s−1 s−1 s−1

1 P1

2

+1

s+1 s+1

Условие идеальности в рассматриваемом случае запишется в виде

c′s′+2 = cs+1 = c′s−1 .

(1.395)

149

Для случая малых концентраций (с << 1) коэффициент разделения ступени соответственно для обогащенной и обедненной фракций с учетом (1.395) можно записать в виде

α =

c′s+1

=

c′s+1

c′s

,

(1.396)

c′s−1

c′s

c′s−1

β

=

c′s−1

=

c′s

=

c′s+1

.

(1.397)

c′s−1

c′′s+1

c′s

По исходному предположению величины α и β не меня-

ются по длине каскада. Комбинируя в этом случае (1.396) и (1.397), получаем, что для любой ступени рассматриваемого каскада выполняются соотношения

α = β 2 ,	(1.398)
q =α β = β3 .	(1.399)

Решая уравнения (1.396) и (1.397) с граничным условием c1′ = β3cW и с учетом соотношений (1.398) и (1.399), получим

	c′s = cW β s+2,			1 ≤ s ≤ N,		(1.400)
	c′′s = cW β s−1,			1 ≤ s ≤ N.		(1.401)
Из уравнения баланса для произвольной s-й ступени
	cs =θscs′ +(1−θs )cs′′,					(1.402)
имея в виду, что	α =	cs′	, β =	cs	и учитывая соотношение
				cs′′
		cs

(1.399), получим выражение для коэффициента деления потока

	θ		=	β −1	=	β −1		, s =1, 2, ... , N .	(1.403)
		s		q −1		β3 −1

Комбинируя уравнения (1.391) и (1.392) с учетом (1.400) и (1.401), приходим к следующему уравнению, описывающему отвальную часть каскада

150