Борман Теория разделения изотопов 2007

проксимации полученного модельного каскада прямоуголь- но-секционированным или прямоугольным и его оптимизации.

Общий метод расчета модельных каскадов, основан на использовании соотношений, полученных В.Бирюковым [3], Р. Кучеровым и В. Миненко [2] путем замены переменных в уравнениях (2.63), (2.64). Суть перехода на примере отборной части каскада непрерывного профиля состоит в следующем. Из уравнения для компонента i последовательно вычтем уравнения для остальных компонентов, в результате чего получим (m −1) – уравнение типа

d ln ci (s)	−	d ln ck (s)	= ε	ik	−	2PciP		+	2PckP	. (2.85)
ds		ds				L(s)ci	(s)		L(s)ck (s)

Уравнение (2.85) вместе с тождеством (2.1) образует полную систему для определения концентраций компонентов. Легко показать, что системы дифференциальных уравнений (2.63) и (2.85) при условии (2.1) эквивалентны. Если воспользоваться соотношениями (2.5), (2.8) и произвести замену s = SP −l , где l – новая переменная, то уравнения (2.85) мож-

но переписать в виде

d ln Gi

−

d ln Gk

= −ε

ik

+

2PciP

−

2Pcik

.

dl

dl

Gi

Gk

Заменяя

d ln Gi

2PciP

−

=

d ln G

i

,

dl

G

dl

i

приводим уравнения (2.86) к виду

d ln Gi = −εik . dl Gk

В результате получаем

G			i(l)	=		G		k (l)	exp(−ε	ik	s) .
Gi(0)					Gk (0)

(2.86)

(2.87)

(2.88)

(2.89)

201

Решение линейного дифференциального уравнения (2.87) при граничном условии Gi (0) = Gi0 имеет вид

l

G (l)

G (0)

∫

Gi(l) =

i

Gi0

+ 2PciP

i

dt .

(2.90)

G (0)

G (t)

i

0

i

Введем обозначение

ϕ

(l) =

G

i (0)

,

(2.91)

i

Gi(l)

с помощью которого запишем уравнения (2.90) и (2.89) соответственно

						l
Gi(l) ϕi(l) = Gi0 + 2PciP ∫ϕi(t)dt ,								(2.92)
						0
ϕi(l) =ϕk (l) exp(εikl) .								(2.93)
Суммируя в (2.92) по i с учетом (2.8) и (2.93), находим
	m		2Pc	l
Gi (l)ϕi (l) = Gi0 + ∑			iP					;
			L(l)	∫ϕi (t)exp εij			(t −l)
	j=1			0				(2.94)
m	c (0)L(0)
dt = ∑	i					exp(−εijl),
		L(l)
j=1
где L(0) и ci(0) = ciP −	поток и концентрации на отборном

конце каскада при l = 0.

Таким образом, суть перехода состоит в том, что концентрации ci (l) заменяются функциями ϕi (l) , а система уравне-

ний (2.63) при непрерывной функции L(l) приводится к интегральному уравнению Вольтерра с вырожденным ядром [16] и (m −1) алгебраическому соотношению для функций ϕi (l) .

В соответствии с (2.92) функции ϕi(l) связаны с концентрациями и потоком в каскаде соотношением

202

l

L(0)ciP + 2PciP ∫ϕi (t)dt

Gi(l) = L(l)ci	(l) =			0	.	(2.95)
		ϕi	(l)

Следует отметить, что соотношение (2.94) несложно обобщить на случай каскада кусочно-непрерывного профиля, а также наличия нескольких потоков отбора и питания.

При заданном распределении L(l) уравнение (2.94) имеет

единственное решение, которое может быть построено, например, по методу последовательных приближений. Затем по формуле (2.95) можно найти распределение Gi (l) , далее, ис-

пользуя соотношение ci(l) =	Gi	(l)	– распределение кон-
	m
	∑G j (l)

j=1

центраций компонентов смеси.

С практической точки зрения интерес представляет возможность использования (2.95) для нахождения такого распределения L(l) , которое позволяет решить задачу заданного

обогащения целевого компонента. Распределения L(l) и ci (l) по длине каскада однозначно определяются заданием одной из характеристических функций ϕn(l) (остальные ( m −1 )

функций определяются по соотношению (2.93)). Если вид характеристической функции позволяет вычислить интеграл в (2.95), то распределение потока L(l) и концентрации ci(L)

можно получить в аналитическом виде.

Простую и удобную математическую модель, с помощью которой может быть решен широкий круг разделительных задач, можно получить, если задать характеристические функции в виде экспонент

ϕi(l) = exp(Qil) ,

(2.96)

203

где Qi – некоторые постоянные, которые согласно (2.93), должны быть связаны условием

Qi −Q j = εij .

(2.97)

Соответственно, только одна из величин Qi может быть

выбрана произвольно.

Модельные каскады, удовлетворяющие условию (2.96), называют Q -каскадами. В стремлении минимизировать сум-

марный поток каскада естественно принять
L(0) = 0 .	(2.98)

Подставляя (2.96) в соотношения (2.95), учитывая (2.98), а

m

также, что L(l) = ∑G j (l),

j=1

ci (l) = mGi(l) , получаем

∑G j (l)

j=1

2PciP

Gi(l) =

1−exp(−Qil)

,

Q

i

m

c

jP

L(l) = 2P∑

1

−exp(−Q jl)

,

j=1

Q

j

ciP

1−exp(−Qil)

Q

ci(l) =

i

.

m

c

jP

∑

1−exp(−Q jl)

Q

j=1

j

(2.99)

(2.100)

(2.101)

Уравнения (2.99) – (2.101) дают распределение концентраций и потока в отборной части Q -каскада.

Аналогичные уравнения можно записать и для отвальной части каскада:

	2WciW
Gi(l) =		exp(Qil) −1		,	(2.102)
	Q
	i

204

m

c

jW

L(l) = 2W ∑

exp(Q jl) −1

,

j=1

Q

j

ciW

exp(Qil) −

1

Q

ci(l) =

i

.

m

c

jP

∑

exp(Q jl)

−1

Q

j=1

j

(2.103)

(2.104)

l = SW − s .
С помощью полученных	соотношений		(2.99)-(2.100),
(2.102) – (2.103) и выражения	ci (l) =	Gi(l)	можно выра-
		m
		∑G j (l)

j=1

зить концентрации в отборе ciP и в отвале ciW через концентрации в точке подачи питанияciF :

Qici, f

m

Q jc j, f

ciP

=

∑

(2.105)

1

−exp(−Q S

)

1−exp(−Q

S

)

P

j=1

P

Qici, f

i

j

m

Q jc j, f

ciW

=

∑

.

(2.106)

exp(Q S

) −1

exp(Q S

) −1

W

j=1

i

j

W

Следует подчеркнуть, что концентрации в точке подачи питания каскада ci, f в общем случае не равны концентрациям

в потоке питания ciF . Используя уравнения материальных

балансов (2.43), можно из уравнений (2.105) и (2.106) исключить ci, f и выразитьciP и ciW через концентрации в потоке

питания

ciP =

1−exp(QiSW )

ciF ×

exp(−Q S

P

) −exp(Q S

)

i

i

W

(2.107)

m

1−exp(−Q jSW )

−1

×

∑

c jF

;

exp(−Q

S

)

−exp(Q

S

)

P

W

j=1

j

j

205

ciW

=

exp(−QiSP) −1

ciF ×

exp(−Q S

P

) −exp(Q S

)

i

i

W

(2.108)

m

exp(−Q jSP) −1

−1

×

∑

c jF

.

exp(−Q

S

) −exp(Q

S

)

P

W

j=1

j

j

В свою очередь, используя формулы (2.100), (2.103), а также уравнения баланса (2.43) и очевидное соотношение

m

∑c j =1, легко получить следующее выражение:

j=1

W

m

1−exp(Q jSP)

= ∑

c jF .

(2.109)

P

exp(Q S

) −exp(−Q

S

)

j=1

P

j W

j

F

m

exp(Q jSW ) −1

= ∑

c jF .

(2.110)

P

exp(Q S

) −exp(−Q

S

)

j=1

P

j W

j

Полученные формулы (2.107) и (2.108) показывают, что Q -каскады позволяют проанализировать процесс концентрирования изотопов в определенной части изотопного спектра при соответствующем выборе величины Qi . Это вытекает из следующих рассуждений. Предположим для определенности, что для i -го изотопа параметр Qi > 0 . Кроме того, естествен-

но принять, что мы имеем дело с длинными каскадами, у которых SP и SW велики. При оценке эффекта разделения на-

блюдается различие в поведении компонентов, для которых Qn больше или меньше нуля.

Для случая Qi > 0 из выражения (2.107) в предположении, что знаменатели в этих формулах одинаковы, нетрудно полу-

чить оценочные соотношения:
	ciP	≈	ciF	,	(2.111)
	c jP
			c jF

206

аналогично, если Qi < 0 , то на основании выражения (2.107) запишем

ciP	>>	ciF	.	(2.112)
c jP
		c jF

Для отвальной части каскада аналогичные оценки получаются при Qi < 0 . В соответствии с условием (2.97) и учиты-

вая, что выражение для коэффициента εik можно представить в виде εik = ε0(M k − M i ) , постоянную Qi для любого компонента i =1, m можно записать как

Qi = ε0(M − M i ) ,

(2.113)

где M – параметр, задание которого позволяет определить одновременно постоянную Q для всех компонентов смеси, ε0 – коэффициент обогащения, приходящийся на единичную разность массовых чисел, Mi – массовое число i -го компонента

смеси. Тогда согласно выражению (2.113) все концентрации компонентов с массовыми числами Mi < M будут возрас-

тать, концентрации компонентов с массовыми числами Mi < M – падать на отборном конце каскада. Следовательно,

Q -каскады позволяют разделять все изотопы данного эле-

мента на две группы, причем в первой группе концентрации всех компонентов одновременно растут, а во второй группе падают.

Из полученных результатов непосредственно следует, что в одном Q -каскаде нельзя неограниченно увеличивать кон-

центрацию промежуточного компонента в отборе, поскольку сумма концентрации обогащаемых изотопов не должна превышать единицу.

С использованием (2.107) можно записать формулу для отношения концентраций любых i - и n -го компонентов в отборе Q -каскада:

207

ciP

=

exp(QiSW ) −1

exp(QnSW ) −exp(−QnSP)

ciF

. (2.114)

c

nP

exp(Q S

W

) −1

exp(Q S

) −exp(−Q S

P

)

c

nF

n

i W

i

Если n – номер целевого компонента и компоненты пронумерованы в порядке возрастания массовых чисел, Qi выби-

рается так, чтобы все значения при i ≥ n были меньше 0. Тогда для каскадов с достаточно длинной обогатительной сек-

цией, т.е. при любом i , exp Qi SP >>1 (см. формулу (2.114)),

получим предельное значение целевого изотопа при выбранном числе ступеней в обеднительной части каскада SW :

cnP ≈

cnF

,

(2.115)

n

∑γiciF

i=1

где

γ

i

=

1−exp(−QiSW )

.

(2.116)

1−exp(−QnSP)

При этом число ступеней

SW

и концентрация целевого

компонента cnW в потоке отвала связаны соотношением

cnW ≈

cnF exp(−QnSW )

.

(2.117)

n

m

∑ciF exp(−QnSW ) + ∑ ciF

j=1

i=n+1

В предельном случае при SW →∞ формула (2.117) получа-

ет вид (2.66), а при SW →0

cnF

cпP ≈

,

(2.118)

n

Q

∑

i

ciF

Q

i=1

n

причем Qi Qn ≥1

(i =1, 2,K, n) . Таким образом, максималь-

но допустимое значение концентрации cпP при наличии обеднительной части определяется соотношением

208

	cnF				< c		<	cnF	.	(2.119)
n						nP
	Q							n
∑		i		ciF				∑ciF
	Q
i=1		n						i=1

В случае если целевой компонент обогащается в противоположенной части каскада с компонентами, номера которых i = n +1,K, m (т.е. в потоке W ), то соотношение (2.119) пере-

пишется в виде		cnF					cnF
				< c		<		.	(2.120)
	n				nW
		Q					n
	∑	i	ciF				∑ciF
	i=1	Qn					i=1

Предельные значения промежуточных компонентов на концах Q -каскада существенно зависят от исходного состава.

Так, для изотопной смеси изотопов вольфрама природного состава (табл. 2.2) предельные значения концентрации изото-

па W −183 ( i = 3) составляют c3P ≈ 35,11%, c3W =19, 43% , а

предельные значения	концентраций			изотопа		W −185
( i = 4) : c4P ≈ 42, 95%, c4W = 51, 75% .					Таблица 2.2
Природная распространенность изотопов вольфрама
Номер компонента, i		1	2	3	4		5
Массовое число изотопа		180	182	183	185		186
Концентрация, ciF , %		0,13	26,30	14,30	30,67		28,60

Для получения значений концентраций целевых промежуточных изотопов больших, чем предельные значения этих концентраций на концах каскада, имеются две возможности.

1. Подключение дополнительного отбора на том участке каскада, где целевой компонент локализуется. Анализ показывает, что в данном случае концентрация целевого компонента ненамного превосходит величину, определяемую соотношением (2.119).

209

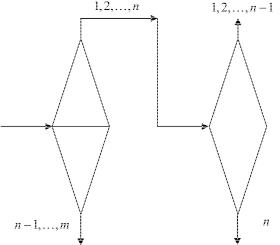
Рис. 2.6. Схема выделения в двух последовательно соединенных каскадах промежуточного компонента

Задача о получении любого практически чистого промежуточного компонента решается с помощью двух последовательно соединенных Q -каскадов (рис.2.6).

Важной интегральной характеристикой разделительного каскада является суммарный поток. Умножив (2.101) и (2.103) на dl и проинтегрировав (2.101) и (2.103) соответственно по длине отборной и отвальной части, получим формулу для суммарного потока:

m

+Wc

Pc exp(−Q S

P

) −1

exp(Q S

) −1

∑L = 2∑

iP

i

iW

i W

+

2

i

i=1

Q

(2.121)

Pc S

−Wc

S

p

w

+

iP

iW

.

Q

i

Для расчета Q -каскада на заданные величины cnP,

cnW и

P (n – номер целевого компонента; все величины εij

и ciF

210