Борман Теория разделения изотопов 2007

RS′ = qS RS′′,	(1.89)
и степень разделения в каскаде Q = RN′ / R1′′	достигает макси-
мальной величины
N
Q = ∏qS ,	(1.90)

S =1

где RN′ и R1′′ – относительные концентрации ценного (целе-

вого) изотопа на концах каскада. Если все ступени в каскаде имеют одинаковые полные коэффициенты разделения, т.е. qS ≡ q , то соотношение (1.90) может быть преобразовано к

виду

N = ln Q / ln q ,

(1.91)

известному как формула Фенске [12]. Она определяет минимально возможное число ступеней, необходимое для достижения заданного значения степени разделения каскада. Характерно, что число ступеней в каскаде N не зависит от формы каскада, т.е. конкретного распределения LS .

В случае слабых одинаковых обогащений на ступенях из (1.85) и (1.86) для безотборного режима каскада имеем

dc	= εc(1 − c) ,	(1.92)
ds

откуда после интегрирования получаем экспоненциальный закон изменения концентраций по ступеням

R2 = R1 exp(εs12) ,

(1.93)

здесь R1, R2 – относительные концентрации ступеней, рабо-

тающих на участке каскада, определяемом концентрациями c1 и c2; s12 – соответствующее количество ступеней. В режимах работы каскада с непрерывным отбором и отвалом (P ≠ 0, W ≠ 0) изменения концентраций на ступенях, а, сле-

довательно, и степень разделения каскада будут меньше.

51

1.5.Критерии эффективности работы каскада

Взадачах проектирования каскадов целесообразно определять их параметры, исходя из принятого критерия эффективности. Возможны два принципиальных подхода к выбору критериев.

Первый подход предполагает, что параметры ступеней могут быть выбраны из физических соображений, не связанных непосредственно с поставленной целью разделения. Физический критерий эффективности выражается требованием, чтобы энтропия при соединении потоков на входе каждой ступени не возрастала, т.е. чтобы термодинамическая работа, связанная с изменением концентрации при разделении смеси, не терялась. Для этого необходимо, чтобы концентрации различных потоков на входе в каждую ступень были одинаковыми. Для каскада с тремя внешними потоками, представленного на рис. 1.5, это соответствует выполнению условий

c′S −1 = cS	= c′S′+1,		(1.94)
c f	= cF ,
или
RS′−1 = RS	= RS′′+1	,	(1.95)
R f	= RF .

Соотношения (1.94), (1.95) называются условиями несмешения, а каскад, удовлетворяющий этим требованиям, – иде-

альным.

В другом подходе определяют практические потребности изотопного производства. Создание крупного разделительного предприятия (завода) связано с минимизацией удельных материальных затрат на производство обогащенного продукта. Эта задача весьма сложная в силу того, что необходимо определить большое число параметров, влияющих на затраты производства. Задачу оптимизации каскада можно упростить,

52

учитывая специфику метода разделения. В общем случае задача оптимизации может быть записана в виде

		ψ = ψ (u1, u2 ,..., uk ) → min(max),	(1.96)
где	Ψ –	целевая функция (показатель эффективности);
u1,	u2, ...,	uk – независимые параметры каскада;	min(max) –

значение целевой функции (минимум или максимум) при оптимальных значениях независимых параметров. При использовании молекулярно-кинетических методов разделения удельные затраты на производство обогащённого продукта, как правило, пропорциональны суммарному количеству элементов в каскаде. В соответствии с этим при заданных внешних параметрах в качестве критерия оптимизации можно принять минимум суммарного количества разделительных элементов:

N
Ψ = ∑ZS → min,	(1.97)

s=1

где ZS – число разделительных элементов в s-й ступени кас-

	N
	када. Величина ∑ZS при работе элементов с заданными
	s=1
	одинаковыми потоками LЭ может быть представлена в виде
		N
	n	∑LS
	∑ZS =	s=1	(1.98)
		LЭ
	s=1

и, следовательно, в этом случае целью оптимизации является минимизация суммарного потока питания ступеней

N
ψ = ∑LS → min .	(1.99)

s=1

Данный критерий предусматривает, что все внешние параметры каскада варьируются в допустимой области их изменения до получения минимального суммарного потока. Каскад, отвечающий требованию (1.99), будем называть опти-

мальным.

53

1.6.Идеальный каскад для разделения бинарной изотопной смеси [1–5, 13–15, 19]

1.6.1.Основные уравнения симметричного идеального каскада. Классификация идеальных каскадов

Условие (1.94) позволяет однозначно определить распределение потоков в идеальном каскаде. Перепишем условие (1.94) в виде двух равенств:

δS′−1 = ∆S −1, ∆S =δS′′+1

(1.100)

или, в первом из них, смещая индексы и используя в виде единого соотношения, получим

δ′	= ∆	S	= δ′′	+1	.	(1.101)
S			S

Подставляя (1.101) в (1.80) и обозначая поток в идеальном каскаде через L*S , получим

L*	=	P(cP −cS )					,
S		θSδS′							(1.102)
s = f , f +1,							...,		N −1,
		L*	=				P	.	(1.103)
		N		θ
							N

Аналогично распределение потоков в обеднительной части идеального каскада можно представить в виде

L* =	W (cS − cW )						,	(1.104)
S			θ δ′
					S S
L*		=			W	.		(1.105)
1			1		−θ1

Величина обогащения на ступени δS определяется соот-

ношением (1.9), а коэффициент деления потоков формулой (1.48). Таким образом, систему уравнений, позволяющую рассчитывать распределения концентраций, коэффициентов деления потоков и расходов в идеальном каскаде, можно представить в виде:

54

(α

S

−1)c

S

(1 − c

S

)

ε

′ c

S

(1 − c

S

)

∆ = c

S +1

− c

S

=

=

S

,

S

1

+ (αS

−1)cS

1 + εS′ cS

]

(β

S

−1)[1

+ (α

S

−1)c

S

ε′′(1+ε′c

S

)

θS =

=

S

S

,

qS −1

(1 −εS′′)εS

	*		P(cP − cS )
	L	=
			θ δ′
	S
			S S

L* =W (cS − cW )

S θSδS′

–для обогатительной части каскада,

–для обеднительной части каскада,

(1.106)

(1.107)

(1.108)

(1.109)

с граничными условиями
θN L*N = P,	c′n = cP ,	(1.110)
(1−θ1)L1* =W,	c1′′ = cW ,	(1.111)

образуют полную систему. Кроме того, к условиям (1.110), (1.111) необходимо добавить условие несмешения концентраций на входе в ступень питания cF = cf .

Обратим внимание на тот факт, что система (1.106) – (1.109) записана в конечных разностях и её следует решать "шаг за шагом".

Наиболее изученными и имеющими практическое значение являются свойства идеального каскада при малых обогащениях на отдельных ступенях (случай слабого обогащения).

1.6.2.Идеальный каскад с малым обогащением на ступени (случай слабого обогащения) [1–5, 78]

В случае «слабых обогащений» на ступенях формулы

(1.106) – (1.109) упрощаются. Тогда с учетом (1.82), (1.10) – (1.12) и факта, что параметры каскада от ступени к ступени изменяются непрерывно, система (1.106) – (1.109) приводится к виду:

dc	= 1	εc(1− c),	(1.112)
ds	2

55

		θ ≈ 1 ,		(1.113)
		2
*			4P(cP − c)
L	=			(1.114)
			εc(1 − c)

для обогатительной части каскада

*		4W (c − cW )
L	=		(1.115)
		εc(1− c)

обеднительной части каскада.

Из уравнения (1.112) следует, что градиент концентрации в идеальном каскаде вдвое меньше, чем при безотборном режиме работы каскада.

Уравнение (1.112) легко интегрируется и дает распределение c(s) , а уравнения (1.114) и (1.115) дают распределения

L* (s) , выраженные через параметр c(s) . Уравнения (1.112) – (1.115), называют уравнениями идеального симметричного

каскада. Как видно из (1.112) и (1.115), потоки L* обратно пропорциональны ε . Этот факт существенен для практики.

	Так, для газодиффузионного метода разделения							ε ~ 10−3
	[3, 7] и, следовательно,	потоки (производительности) ступе-
	ней должны в тысячи раз превышать потоки отбора P и отва-
	ла W. Интегрирование уравнения (1.112) для любого интерва-
	ла концентраций c1 ≤ c ≤ c2			дает соответствующее число сту-
	пеней		2		c2 /1−c2
	s	=		ln			.	(1.116)
	12		ε		c /1	−c
	Полагая c1 равным cW			1		1
				или cF		и c2 равным cF		или cP ,

можно получить формулы для расчета числа ступеней в обеднительной и обогатительной части каскада соответственно.

56

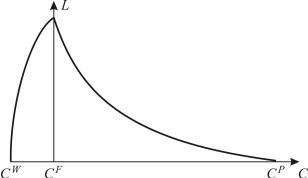
Рис. 1.9. Зависимость потока L* от концентрации

На рис. 1.9 показана зависимость потока питания ступеней от концентрации. Выбранный случай характерен для разделения изотопов урана и других элементов с низким содержанием ценного компонента cF <<1. В секции обогащения изме-

нение потоков (формула 1.114) имеет гиперболический характер. Потоки уменьшаются от ступени питания в сторону отбора с постоянно снижающейся скоростью. В отличие от этого в секции обеднения небольшое уменьшение вблизи ступени питания сменяется резким спадом у отвала каскада.

Закономерен вопрос: соответствует ли идеальному каскаду наименьший суммарный поток? Для ответа на него вычислим

сумму ∑L в обогатительной части каскада (в обеднитель-

ной части каскада, как нетрудно убедиться, результат будут аналогичен).

CP	Ldc		CP		L(c)dc
∑L = ∫			= ∫						=
	dc / ds			εc(1−c) −		2P(cP −c)
CF			CF				L(c)		(1.117)
	CP
				2	(c)dc
= ∫			2L					.
					*		(c)
	CF	εc(1−c) 2L(c) − L
									57

В этой формуле внешние параметры каскада P, cP , cF (в обеднительной части также cW ) следует считать заданными.

Интеграл (1.117) будет иметь минимальное значение, если при любом возможном значении концентрации c подынтегральная функция минимальна. Отсюда следует, что для нахождения оптимального потока в отборной части каскада следует воспользоваться следующим уравнением

	d				L2
							= 0 .	(1.118)
					*
	dL			2L − L
Из (1.118) следует, что
			L		= L* .			(1.119)
				опт

Таким образом, в соответствии с равенством (1.119) в случае слабого обогащения идеальный каскад обладает свойством оптимальности. Его суммарный поток и распределение потоков по ступеням соответствует каскаду, оптимальному по критерию минимума суммарного потока. Полученные ре-

зультаты позволяют без особых трудностей выразить ∑L* в идеальном каскаде через внешние параметры каскада. Для нахождения суммарного потока ∑L* следует вычислить ин-

теграл, подобный (1.117), для всего идеального каскада, включая обеднительную часть:

CP

*

CP

8P(cP −c)

IP = ∫

L

dc = ∫

dc =

dc

ε

2

c

2

(1−c)

2

CF

CF

(1.120)

ds

ид

8P

c

P

(1

−c

F

)

(1

−2c

F

)(c

P

−c

F

)

=

2

(2c

p

−1) ln

+

.

ε

c (1−c )

c (1−c )

F

P

F

F

58

CP

*

CP

8W (c −c )

IW = ∫

L

dc = ∫

W

dc =

dc

2 2

2

CF

CF

ε c

(1−c)

(1.121)

ds ид

8W

cW

(1−cF )

(1−2cF )(cW −cF )

=

(2c

−1) ln

+

.

ε 2

(1−c )

W

c

c (1−c )

F

W

F

F

Складывая (1.120) и (1.121) и учитывая общие соотношения (1.77) и (1.78), получим после алгебраических упрощений

∑L* =

8

c

P

P(2c

p

−1) ln

+W (2c

−1)×

ε 2

1−c

P

W

. (1.122)

c

c

F

×l n

W

− F(2cF −1) ln

1−c

1

−c

W

F

Используя формулу (1.28) для разделительного потенциала, (1.122) можно переписать в виде

∑	L*ε2	= PV (cP ) + WV (cF ) − FV (cW ) . (1.123)
8

Соотношение (1.123) имеет фундаментальное значение в теории каскадов. Его левая часть представляет собой сумму разделительных способностей ступеней, образующих идеальный каскад, и определяется их разделительными характери-

стиками. Правая часть ∆U = P(2c

p

−1) ln

cP

+W(2c −1) ×

1

W

cW

cF

− cP

×ln

− F(2c −1) ln

определяется

внешними пара-

1 − cW

F

1

− cF

метрами. Разделительные характеристики в это выражение не входят. Поэтому правая часть может рассматриваться как внешняя нагрузка, на которую работает каскад. Согласно (1.123), сумма разделительных способностей ступеней идеального каскада должна равняться внешней нагрузке, которую можно интерпретировать как полезную разделительную

59

работу в единицу времени (разделительную способность), которую совершает каскад. Выражение (1.123) легко получить исходя непосредственно из понятия разделительной способности ступени и связанного с ним соотношения (1.17). Это соотношение для произвольной s-й ступени каскада можно переписать в виде

δU S =θS LSV (cS +δS′ ) +(1−θS )LSV (cS −δS′′) − LSV (cS ) . (1.124)

Просуммируем (1.124) по всем ступеням каскада. Поскольку в каскаде отсутствуют потери на смешение, то левая часть соотношения (1.124) будет представлять собой суммарную разделительную способность всех ступеней каскада, т.е.

∑δUS . При суммировании выражения в правой части следу-

ет учитывать, что при соединении потоков в идеальном каскаде концентрации в них должны быть одинаковыми и что, следовательно, каждому потоку, исходящему из одной ступени, будет соответствовать поток, входящий в другую ступень (но с обратным знаком). При суммировании все внутренние потоки пропадут и останутся три внешних – W, F и P, каждый со своей концентрацией. Таким образом, снова получается соотношение, аналогичное (1.123):

∑δUS = PV (cP ) +WV (cW ) − FV (cF ) .

(1.125)

Такой подход к выводу (1.125) имеет целью подчеркнуть обстоятельство, непосредственно не вытекающее из предыдущего вывода: в рассматриваемом соотношении коэффициенты разделения отдельных ступеней могут быть различными. Кроме того, из проведенного рассуждения следует, что формально в качестве потенциала разделения V (c) может

быть выбрана произвольная непрерывная функция переменной c. Однако для расчета суммарного числа элементов в каскаде соотношение (1.125) может быть использовано только в том случае, когда элементы, составляющие каскад, идентичны и разделительная способность δUЭЛ от концентрации не

60