считаем известными) можно рекомендовать следующую последовательность расчета:
1.Для целевого компонента задаем величину Qn (точнее,
всоответствии с (2.113) величину M .
2.По соотношению (2.113) определяем все остальные Qi .
3. Решая совместно (2.107) – (2.108) для i = n , находим
SP и SW . |
|
4. Далее по |
(2.107)-(2.108) находим все остальные |
ciP (i ≠ n) и ciW |
(i ≠ n) , а по (2.109) и (110) потоки отвала и |
питания. |
|
5.По формулам (2.100) и (2.103) определяем распределения потоков в отборной и отвальной частях каскада, а соотношение (2.121) позволяет вычислить суммарный поток каскада.
6.Оптимальную величину М следует определять из усло-
вия ∑L = min .
На рис.2.7 представлена зависимость относительного суммарного потока ε0∑L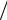 2P Q-каскада, разделяющего природ-
2P Q-каскада, разделяющего природ-
ную смесь изотопов криптона (см. табл. 2.3), от величины параметра М при фиксированном значении концентрации ключевого компонента 78Kr в потоке отвала c1W =0,12 для трех
значений концентрации этого компонента в потоке отбора: c1P =20% (кривая 1), c1P =30% (кривая 2) и c1P =50% (кри-
вая 3).
Таблица 2.3
Природный состав изотопов криптона.
|
|
|
|
|
|
|
Номер компонента |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
|
|
Изотоп |
78Kr |
80Kr |
82Kr |
83Kr |
84Kr |
86Kr |
|
|
|
|
|
|
|
Концентрация, ciF , % |
0,35 |
2,27 |
11,56 |
11,52 |
56,90 |
17,40 |
|
|
|
|
|
|
|
Все кривые имеют минимум. Отметим, что в каждом случае оптимальная величина параметра М, соответствующая минимуму суммарного потока, равна полусумме величин массовых чисел ключевого компонента и одного из соседних
компонентов. Для кривой 1 Мопт = 81 = (М1 + М5)/2 = (78 + + 84)/2, для кривой 2 Мопт = 80,51 = (М1 + М4)/2 = (78 + 834)/2, а для кривой 3 Мопт = 80 = (М1 + М3)/2 = (78 + 82)/2.
Из информации, приведенной в разделе 2.3.4.2, станет ясно, что в рассмотренных примерах оптимальные условия разделения соответствуют Q-каскадам, на входах в ступени которых имеет место несмешение по относительным концентрациям Rnk = cn 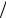 ck , где n – номер ключевого (целевого)
ck , где n – номер ключевого (целевого)
компонента, k – номер опорного компонента, выбор которого для каждого примера обеспечивает условие ∑L = min .
Рис. 2.7. Зависимость относительного суммарного потока в Q-каскаде при обогащении 78 Kr от величины параметра M. Кривая 1 для C1P = 20% , 2 для C1P = 30% и 3 для C1P = 50%
Отметим, что для получения по формулам (2.101), (2.102), может быть использован подход, предложенный Б.В. Жигаловским [3]. В нем автор постулирует, что срезы парциальных потоков в каскаде могут быть представлены в виде
ϕ |
i |
= |
1 (1 |
+ε |
), 1 =1, 2, ..., m , |
(2.122) |
|
|
2 |
i |
|
|
|
|
|
|
|
|
где εi – константы, не меняющиеся по величине при перехо-
де от ступени к ступени.
Нумеруя, как и раньше, ступени отборной части каскада от отборного конца к точке подачи питания, обозначим поток i-го компонента, проходящий через сечение между (l +1) -й и
l-й ступенями через Ji = PciP . Тогда в отсутствие потерь на ступенях балансовые уравнения можно записать в виде
|
|
′ |
|
|
|
′′ |
|
|
|
|
|
|
|
|
i =1, 2, ..., m |
(2.123) |
|
|
Gi(l +1) −Gi |
(l) = Ji, |
|
|
или |
|
|
|
ϕiGi(l +1) −(1−ϕi )Gi(l) = Ji. |
(2.124) |
С учетом (2.122) уравнения (2.124) преобразуются к виду |
G (l +1) −G (l) = 2 |
|
εi |
|
|
|
G |
(l) + |
|
|
2Ji |
|
, i =1, 2, ..., m . (2.125) |
1+ε |
|
|
1+ε |
|
i |
|
i |
i |
|
i |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для случая, когда εi |
|
<<1, уравнение (2.125) можно пере- |
писать в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dGi |
== −2ε |
|
G |
+ 2J |
|
, |
|
|
i =1, 2, ..., m . |
(2.126) |
|
|
|
|
|
|
|
|
|
|
dl |
|
|
i |
|
|
|
i |
|
|
|
i |
|
|
|
|
|
|
|
Решение |
|
этого |
уравнения, |
|
|
|
удовлетворяющее |
условию |
Gi(0) = PciP , есть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
(l) = |
PciP |
|
1−exp(−2ε |
i |
l) , |
i =1, 2, ..., m. |
(2.127) |
|
|
i |
|
|
|
εi |
( |
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
Полный поток через ступень определяется выражением |
|
|
|
|
|
|
m |
|
|
c |
jP |
|
|
|
|
|
|
|
|
|
|
|
L(l) = P∑ |
|
|
1 |
−exp(−2ε jl) . |
(2.128) |
|
|
|
ε |
|
|
|
|
|
|
|
j=1 |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для концентрации i-го компонента получаем выражение:
ci(l) = mGi (l)
∑G j (l)
j=1
|
|
ciP |
|
|
|
|
|
|
|
|
1−exp(−2εil) |
|
= |
|
ε |
i |
|
|
|
|
|
|
|
|
|
. |
(129) |
m |
c |
|
|
|
|
|
∑ |
|
|
jP |
1 |
−exp(−2ε jl) |
|
|
|
|
|
|
j=1 |
|
ε |
|
|
|
|
|
|
|
|
i |
|
|
|
Каскад, производительность ступени которого определяется формулой (2.128), в работе [3] назван «свободным» каска-
дом. Сравнение (2.99) и (2.127), (2.100) и (2.128), (2.101) и (2.129) показывает, что при условии Qi ≡ 2εi введенные выше
понятия Q − каскада и «свободного» каскада идентичны.
На примере диффузионной ступени в работе [3] выявлен
физический смысл констант εi (или Qi ). |
|
εi −εk = ε′ik = εik / 2 , |
(2.130) |
то есть 2εi ≡ Qi, 2εk ≡ Qk .
Определение «свободный» каскад согласно [3] означает, что суммарный (по всем компонентам смеси) поток L(l) от
ступени к ступени изменяется в соответствии с изменением величины потока каждого из компонентов при прохождении через разделительную ступень. При этом перенос каждого компонента не зависит от переноса других компонентов.
2.3.4.2. R-каскады и их свойства
В случае многокомпонентной смеси создать каскад, в котором не происходит смешения потоков с разными концентрациями всех компонентов или нескольких (больше 2) компонентов невозможно, строго говоря, вследствие различия в величинах Qi (или εi ), определяющих изменения количества
i-ого компонента при движении по каскаду. Однако, как показывает анализ соотношений (2.100) – (2.108) и (2.113), можно, оставаясь в рамках Q − каскадов («свободных» каскадов)
построить такие каскады, в которых не происходит смешения по парам концентраций cn и ck (точнее по относительным
концентрациям Rnk = cn /ck ). Очевидно, должно существовать
m (m −1) каскадов для m – компонентов смеси, каждый из
2
которых для пары произвольных компонентов ( cn , ck ) явля-
ется «идеальным». Покажем, что случай
M ≡ M * = M n + M k
2
соответствует каскаду, на входах в ступени которого смешиваются потоки с одинаковым отношением концентраций n-го и k-го компонентов Rnk = cn / ck . Такой каскад, детально изу-
ченный для 3-компонентной изотопной смеси в классической работе [13] был назван R-каскадом. Если параметр М задан в виде (2.131), то выражение (113) может быть переписано в виде
Q = ε |
( |
M n + M k |
− M |
) |
(2.132) |
|
i |
0 |
2 |
|
i |
|
|
|
|
|
|
|
и в частности, |
|
Qk = −Qn . |
|
|
(2.133) |
При задании Qi в виде (2.132) из (2.107) и (2.108) с учетом уравнений баланса (2.43) можно непосредственно получить
RP |
≡ |
cnP |
|
|
cnF |
|
= exp(Q |
S |
p |
) ; |
(2.134) |
|
|
|
|
|
nk |
|
|
ck P |
|
|
ck F |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
RW |
≡ |
cnW |
|
|
cnF |
|
= exp(−Q S |
W |
) , |
(2.135) |
|
|
nk |
|
ckW |
|
ck F |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
где индексы P и W показывают, что значения относительных концентраций Rnk взяты для потоков отбора и отвала соот-
ветственно.
Уравнения (2.134) и (2.135) означают, что в выбранном
|
каскаде относительные концентрации R |
nk |
= |
cn |
на входах в |
|
ck |
|
|
|
|
|
|
|
|
|
разделительную ступень одинаковы, т.е. выполняется условие несмешивания относительных концентраций Rnk .
Из соотношений (2.134) и (2.135) следует, что задание относительных концентраций Rnk в потоках отбора и отвала
позволяет однозначно определить количество ступеней SP и SW , и следовательно, в соответствии с формулами (2.99) –
(2.104), (2.107) – (2.110) полностью рассчитать каскад. Одновременно при задании Qi в виде (2.132) выражение
для суммарного потока (2.121) существенно упрощается. Действительно, из (2.107) и (2.108) с учетом условия (2.133) имеем
Pc |
|
(exp(−Q S |
|
) −1) = −Pc |
|
ci, f |
|
Qi |
(exp(Q S |
|
−1)) (2.136) |
iP |
P |
k P c |
|
Q |
P |
|
i |
|
k, f |
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
Pc |
|
(exp(Q S |
|
) −1) |
= −Wc |
|
ci, f |
|
Qi |
(exp(Q S |
|
−1)) . (2.137) |
iW |
W |
k W c |
|
Q |
W |
|
i |
|
|
k, f |
|
n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
Суммируя (2.136) и (2.137) с учетом (2.43), (2.134) и (2.135), можно получить равенство
PciP(exp(−QiSP −1)) +WciW (exp(QiSW −1)) = 0 , |
(2.138) |
справедливое для любого i. Кроме того, непосредственно из |
соотношений (2.134), (2.135) с учетом уравнений |
баланса |
(2.43) следует:
|
Pc S |
P |
−Wc S |
Pc ln RP |
+Wc |
ln RW |
−Fc |
ln RF |
|
iP |
|
iW |
W |
= |
|
iP |
nk |
|
|
iW |
|
nk |
iF |
nk |
,(2.139) |
|
|
|
Qi |
|
|
|
|
|
|
|
QiQn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где RP |
= |
cnP |
, |
RW |
= |
cnW |
, |
RF |
= |
cnF |
. |
|
|
|
|
|
|
|
|
|
|
nk |
|
ckP |
|
nk |
|
ckW |
|
nF |
|
ckF |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставив соотношения (2.138) и (2.139) в выражение для суммарного потока (2.121) и заменив Qn и Qi по формулам
(2.131), (2.132), получим
|
2 |
m |
Pc |
jP |
ln RP |
+Wc |
jW |
ln RW |
− F ln RF |
∑L = |
∑ |
|
nk |
|
|
nk |
iF nk |
. (2.140) |
2 |
|
|
|
M − M |
|
|
|
ε |
|
|
|
|
|
|
|
|
|
0 j=1 |
|
(M k − M n) |
|
k |
|
n |
− M j |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение (2.130) с учетом (2.134), (2.135) и (2.43) легко преобразуется к виду
PciP (RnkP )−di +WciW (RnkW )−di − FciF (RnkF )−di = 0 ,
|
|
|
|
Qi |
(2.141) |
|
d |
i |
= |
, i =1.K, m, i ≠ n, k. |
|
Qn |
|
|
|
|
|
|
|
|
|
Уравнения (2.141), связывающие внешние потоки R- каскада и концентрации компонентов в этих потоках, носят названия Н-баланса [13]. Следует иметь в виду, что уравнения (2.141) содержат m − 2 независимых соотношений, так как при i = n и i = k они трансформируются в уравнения покомпонентного баланса для n-го и k-го компонента. Уравнения (2.141), совместно с уравнениями покомпонентного баланса (2.43) (m уравнений) и очевидными соотношениями
m |
m |
∑c jP =1 и |
∑c jW =1 образуют систему m − 2 + m + 2 = 2m |
j=1 |
j=1 |
независимых алгебраических уравнений, содержащую 2m + 3 неизвестных параметра ( 2m выходных концентраций: ciP и
ciW , потоки P, W и F). Таким образом, проектировочный расчет R-каскада предполагает задание (2m + 3) − 2m = 3 параметров (например, ciP , ciW и P), остальные параметры опре-
деляются из решения указанной алгебраической системы.
В разделительной практике могут встречаться варианты расчета каскада из заданного числа разделительных элемен-
тов, т.е. каскадов с известным суммарным потоком. В этом случае система алгебраических уравнений должна быть дополнена уравнением (2.140), после чего для её решения достаточно задать лишь два параметра (например, cnP и P).
Заметим, что при k = n +1 получается R-каскад, позволяющий выделять в потоке отбора целевой (n-й) компонент вместе с 1-м, 2-м, …, (n-1)-м компонентами и препятствовать появлению в этом потоке компонентов с номерами n + 1, n + 2, … , m.
Рассмотренный частный случай Q-каскада (R-каскад) при переходе к двухкомпонентной смеси позволяет получить формулы для идеального каскада без смешения концентраций на входах в ступень. Это непосредственно следует из формул (2.134), (2.135). Легко показать, что в этом случае формула для суммарного потока (2.140) также превращается в известную формулу для идеального каскада.
2.3.4.3.Решение системы уравнений каскада с несмешением по относительной концентрации для выбранной пары компонентов методом Б.В. Жигаловского [3]
Рассмотрим некоторую пару компонентов с номерами n и k как опорную. Отсчет ступеней будем вести от отборного конца каскада. Для k-го компонента уравнение обогащения может быть записано в виде
|
|
dck |
|
|
m |
2P (ckP −ck ) |
|
|
|
|
|
= −ck ∑εijc j + |
, |
(2.142) |
|
|
|
|
|
|
|
|
|
|
dl |
|
j=1 |
|
L |
|
|
|
|
где l = SP − s, |
|
SP |
– число ступеней в отборной секции кас- |
када. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение (2.142) перепишем в виде |
|
|
|
|
1 |
|
|
dc |
m |
|
2Pc |
|
2P |
|
|
|
= −∑εijc j + |
|
|
|
|
|
|
|
|
k |
|
kP |
|
− |
L . |
(2.143) |
|
c |
k |
dl |
Lc |
|
|
|
|
|
|
|
j=1 |
|
k |
|
|
|
|
Аналогично для n-го компонента имеем
1 |
|
|
dc |
m |
|
2Pc |
2P |
|
|
= −∑εijc j |
|
|
|
|
|
|
n |
+ |
nP |
− |
L . |
|
c |
n |
|
dl |
Lc |
|
|
|
|
|
j=1 |
|
n |
|
Вычитая (2.142) из (2.143) и учитывая, что |
m |
|
|
|
|
|
m |
(εnj −ε jk )c j = |
−∑ |
(εnj −εkj )c j = −∑ |
j=1 |
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
m |
|
m |
|
|
|
|
|
= ∑εnkc j = −εnk ∑c j = −εnk , |
|
|
|
|
|
j=1 |
|
j=1 |
|
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
dcn |
|
1 |
|
dck |
|
|
|
2P |
|
|
ckP |
|
|
|
|
− |
|
= −ε |
nk |
+ |
|
cnP |
− |
. |
(2.146) |
|
|
|
|
|
|
|
|
|
cn dl |
ck dl |
|
L |
|
|
|
|
|
|
|
|
cn |
|
ck |
|
Примем, что величина потока L равна |
|
|
|
|
|
|
|
4P |
|
|
|
|
ckP |
|
|
L = |
|
|
cnP |
− |
. |
(2.147) |
|
|
|
|
|
|
|
|
|
|
|
cn |
|
ck |
|
|
|
|
εnk |
|
|
|
Подставляя выражение (2.147)в (2.146), получаем |
|
|
d |
|
ln |
cn |
= − |
εnk , |
|
(2.148) |
|
dl |
c |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
откуда, учитывая, что cn(0) = cnP |
и ck (0) = ckP , следует соот- |
ношение |
|
|
|
|
|
|
|
|
|
|
|
c |
n |
= |
c |
nP |
|
− |
ε |
nk |
|
(2.149) |
|
|
exp |
|
|
ck |
ckP |
|
|
|
|
|
|
2 |
|
или |
|
|
|
R |
= |
RP |
exp |
|
εnk |
l |
|
, |
(2.150) |
|
|
|
|
|
|
|
|
|
|
nk |
|
|
nk |
|
|
2 |
|
|
|
|
cn |
|
|
|
cnP |
|
|
|
|
|
|
|
|
где R = |
, |
RP |
= |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nk |
ck |
nk |
|
ckP |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решения (2.149) и (2.150) соответствуют аналогичному решению для двухкомпонентной смеси, разделяемой идеальным каскадом:
|
c |
|
c |
|
ε |
12 |
|
|
|
|
1 |
= |
1P |
exp |
|
l |
, |
(2.151) |
|
c2 |
c2P |
2 |
|
|
|
|
|
|
а соотношение (2.147) является обобщением соотношения для распределения потока в идеальном каскаде:
|
4P |
|
c |
−c |
|
|
|
4P |
c |
|
|
c |
|
|
|
|
L = |
|
|
|
|
1P |
1 |
или |
L = |
|
|
|
1P |
|
− |
|
2P |
|
, |
|
ε |
12 |
|
c (1 |
−c ) |
|
|
|
ε |
12 |
|
c |
|
|
c |
2 |
|
|
|
|
1 |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
где c2 =1−c1, c2P =1−c1P . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдем решение уравнения |
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
dci = −ci ∑εijc j + 2P (ciP −ci ) |
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dl |
|
|
j=1 |
|
|
L(cn, сk ) |
|
|
|
|
|
|
|
где L(cn, сk ) определяется соотношением (2.146) для прочих
компонентов в каскаде с несмешением по Rnk = cn (i ≠ n, k) . ck
Умножая (2.153) на cn , а уравнение для n-го компонента
|
dcn |
m |
2P (cnP −cn) |
|
|
= −cn∑εnjc j + |
(2.154) |
|
dl |
L(cn, ck ) |
|
j=1 |
|
на ci и вычитая (2.153) из (2.154) с учетом того, что поток L(cn, сk ) определяется соотношением (2.147) , получаем
|
d |
|
ci |
|
= ε |
|
ci |
|
− |
εnk |
|
ck |
|
ciP |
/ cnP −ci / cn |
. |
(2.155) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ni |
|
|
|
2 |
|
|
|
|
/ cnP −ck / cn |
|
|
dl cn |
|
cn |
|
cn ckP |
|
Из соотношения (2.149), логарифмируя и дифференцируя,
|
находим |
|
|
|
|
|
|
|
|
|
2 |
1 |
|
ck |
|
|
|
dl = |
d |
. |
(2.156) |
|
|
|
|
|
|
|
εnk ck / cn |
|
|
|
|
|
|
cn |
|
Используя выражение (2.156), преобразуем уравнение
(2.155) к виду

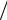 2P Q-каскада, разделяющего природ-
2P Q-каскада, разделяющего природ-
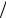 ck , где n – номер ключевого (целевого)
ck , где n – номер ключевого (целевого)


