Борман Теория разделения изотопов 2007

зависит. Тогда разделительную способность s-й ступени можно записать в виде

δU S = ZSδUЭЛ ,

(1.126)

где ZS – число элементов, соединенных в s-й ступени в па-

раллель, а суммарное число элементов в идеальном каскаде составит

	Zид = ∑ZS =	∆U	,	(1.127)
		δUЭЛ
где	∆U = PV (cP ) + WV (cW ) − FV (cF ) .			(1.128)

В случае идеального каскада с малыми одинаковыми коэффициентами обогащения на ступенях, как было установлено ранее, эта величина минимальна, т.е. Zид ≡ Z мин .

Если в соотношении (1.123) W и F выразить через P с помощью уравнений баланса (1.77) и (1.78) и P вынести за скобку, то его можно переписать в виде

∑

L*ε 2

= PΦ(cP, cF , cW ) ,

(1.129)

где

s

8

cP

cP −cF

Φ(c

P

, c

F

,

c

) = (2c

p

−1) ln

+

×

W

1−cP

cF −cW

×(2c

−1) ln

cW

−

cP −cW

(2c

F

−1) ln

cF

.

(1.130)

W

1−cW

cF −cW

1−cF

Функция Φ(cP , cF , cW ) зависит от трех внешних концен-

траций и может быть протабулирована. Соотношение (1.129) представляет разделительную работу, которую совершает идеальный каскад в единицу времени. Тогда для наработки изотопного продукта в количестве P* величина разделительной работы составит

A = P*Φ(c	P	, c	F	, c ) .	(1.131)
				W

61

Из (1.131) следует, что функцию Φ можно рассматривать как выраженную в условных единицах удельную работу разделения, т.е. разделительную работу, необходимую для получения единицы продукта (1 кмоля, 1 кг и т.д.). Функцию Φ называют функцией ценности.

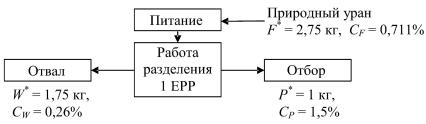
Работа разделения ∆U% , произведенная разделительным каскадом за фиксированное время, может быть найдена как произведение ∆U , рассчитываемого по формуле (1.128), на рассматриваемый период времени. В практических расчетах и на рынке обогащенного урана пользуются условными единицами работы разделения (ЕРР), связанными с количеством произведенного обогащенного металлического урана. За 1 ЕРР принят 1 кг работы разделения (1 ЕРР = 1 кгРР). Эта величина количественно соответствует работе разделения, необходимой для получения 1 кг обогащенного урана с концентрацией 1,5% из 2,75 кг природного сырья при заданной отвальной концентрации 0,26% (рис. 1.10).

Рис. 1.10. Величины параметров разделения, соответствующие 1ЕРР

Разделительная способность каскада обычно измеряется в ЕРР/год. При пересчете в размерность массового потока обычно используют соотношение 1 ЕРР/год = 4,69 г/с, получающееся с учетом различий в массах металлического урана и газообразного гексафторида урана.

Таким образом, в случае «слабого обогащения» на ступенях каскада могут быть сделаны общие выводы:

62

–понятия «идеальный каскад» и «оптимальный каскад» идентичны;

–результаты, следующие из теории идеального каскада и подхода Дирака и Пайерлса, приводят к полезным для практики понятиям «разделительная способность (мощность) ступени», «разделительный потенциал», «функция ценности».

1.6.3.Идеальный каскад с одинаковыми немалыми коэффициентами разделения на ступенях [13–15]

Если принять, что полные коэффициенты разделения ступеней qs каскада одинаковы и не зависят от Ls и θs , то из

общего условия идеальности каскада αs = βs+1 , получающе-

гося из (1.94), (1.95) и (1.6), следует, что идеальный каскад в этом случае характеризуется двумя значениями коэффициентов разделения αs , βs , повторяющимися через ступень:

α1 = β2	=α3 = β4	= ... ,	(1.132)
β1 =α2	= β3 =α4	= ....	(1.133)
Из условия идеальности αs = βs+1 также следует, что

R

s

=α

s−1

R

s−1

=

Rs+1

,

(1.134)

β

s+1

cs

где

Rs =

.

1 − cs

Если расчет ведется, начиная от первой ступени каскада,

то, учитывая условие (1.134), можно записать
R1 = R1′′β1 ,	(1.135)

где R1′′= Rw – относительная концентрация ценного изотопа в потоке отвала. Далее

	R	= R′	= α		R	= α β			R	=	R q ,		(1.136)
	2	1		1	1		1	1	w		w
	R = R′		= α	R		= α	2	qR		= R qβ ,			(1.137)
	3	2		2	2				w		w	1
R	= R′	= α	R = α β R q = R q2									и т.д.	(1.138)
4	3		3 3			1 1	w			w

63

Обобщение выражений (1.135) – (1.138) приводит к следующим формулам для относительных концентраций на входах в ступени идеального каскада:

нечетные ступени:	R = R q		s−1			β	,	(1.139)
			2
	s	w				1
четные ступени:	R	= R q		s		.		(1.140)
				2
	s	w

Анализ соотношений (1.139), (1.140) показывает, что существуют четыре типа идеального каскада, отличающиеся друг от друга числом разделительных ступеней в обогатительной и обеднительной частях и, соответственно, формулами для расчета относительных концентраций Rp и Rw :

тип I: при четном

f -1 и четном N − f +1

N − f +1

q−

f −1

R

= R

q

,

R

= R

β −1;

(1.141)

p

F

2

w

F

2

1

тип II: при четном f -1 и нечетном N − f +1

R

= R

q

N − f +2

−1,

R

= R

q

− f −1

−1;

(1.142)

p

F

2

β

w

F

2

β

1

1

тип III: при нечетном

f

-1 и четном N − f +1

R

= R

q

N − f +1

R

= R

q

− f

(1.143)

p

F

2

,

w

F

2

;

тип IV: при нечетном

f

-1 и нечетном N − f +1

R

= R

q

N − f

R

= R

q

−

f

β ,

(1.144)

p

F

2

w

F

2 .

1

где RF , Rp , Rw – относительные концентрации ценного изо-

топа соответственно в потоке питания, отбора и отвала. Отметим, что при симметричном режиме работы первой

ступени каскада, т.е. при одинаковых коэффициентах разделения по обогащённой и обеднённой фракциям (α1 = β1 ), все ступени каскада будут работать в симметричном режиме. Другими словами, α и β будут одинаковы для всех ступеней каскада и равны

64

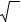
α = β = q .

(1.145)

Идеальный каскад со ступенями, работающими в симметричном режиме, впервые был рассмотрен К.Коэном [1]. В этом случае относительные концентрации не зависят от соотношения числа ступеней в отборной и отвальной частях каскада и формулы (1.139) – (1.144) приводятся к одинаковому виду

R =

R q

s

,

(1.146)

2

s

w

R

N − f +1

−

f

p

= R

F

q 2

, R

w

= R

F

q

2 .

(1.147)

Отметим, что в соответствии с соотношением (1.96) величина параметра β1 и коэффициента деления потока на первой ступени θ1 однозначно связаны. Наиболее простой вид эта связь имеет место при c << 1.

	θ1 =	β1 −1	,	(1.148)
		q −1
	и соответственно
	β1 = 1 +θ1(q −1) .			(1.149)

Как следует из (1.132) и (1.148), величина θs в этом случае

принимает два значения, повторяющиеся через ступень.

В общем случае анализ полученных соотношений (1.141) – (1.144), (1.147) позволяет сделать следующий вывод. При за-

данных величинах q, N, f			и cF (III тип идеального каскада)
или q,	N, f , cF	и β1 (θ1 ) (I, II и IV типы идеального каска-
да)	расчет	каскада	(нахождение	распределений
L(s), θ(s) и c(s) ,		включая концентрации cP		и cW ), труда не

представляет. Причем для III-го типа величины cP и cW не зависят от β1 , т.е. в отношении выбора коэффициента деления потока θ1 существует произвол. При этом при варьировании β1 (или θ1 ) будут меняться распределения β(s) и θ(s) , а

65

вместе с ними и эффективность работы каждой разделительной ступени. Поэтому логично выбирать значение β1 (θ1 ) из

условия оптимальности работы ступеней идеального каскада, которое выполняется при условии минимальности относи-

тельного суммарного потока в каскаде ∑L* / P = min .

Как видно из приведенной зависимости на рис. 1.11, для случая с<<1 минимальный суммарный поток в идеальном каскаде III-го типа, рассчитанном для следующих значений параметров: N = 9, f = 2, cF = 0,711%, cP = 4,4%, cW = 0,45%,

q =1,6 , соответствует случаю, когда он построен из симметричных ступеней, т.е. θ1 =1/ ( q +1).

При расчете каскадов I, II и VI типов с изменением коэффициента деления потока на первой ступени θ1 будет меняться не только величина суммарного потока в каскаде, но и величины концевых концентраций ( cW – в каскаде I-го, cP и cW – в каскаде II-го и cP – в каскаде IV-го типа). Для этих типов идеального каскада каждому значению β1 (θ1 ) соответст-

вует свой идеальный каскад. Расчеты показывают, что и в этом случае из семейства всех возможных идеальных каскадов наименьший суммарный поток будет в каскаде, в котором

выполняется условие β1 = q , т.е. в каскаде из симметрич-

ных элементов.

Задача расчета идеального каскада заметно усложняется в том случае, когда заданы величины q, cP, cW и cF , а требу-

ется найти кроме распределений L(s), θ(s) и c(s) по ступе-

ням каскада также общее количество ступеней N и номер ступени f, в которую подают поток питания. В этом случае решение задачи следует начать с поиска типа идеального каскада, способного обеспечить в выходных потоках значения заданных концентраций cP и cW . Решая систему (1.136) из

66

2-х алгебраических уравнений при заданных значениях концентраций и величине коэффициента разделения q, находим величины N и f. При целочисленных значениях N и f дальнейший расчет идеального каскада из симметричных ступеней труда не представляет. При дробных значениях N и f необходимо подобрать тот тип идеального каскада, который при соответствующем подборе целочисленных величин N и f, а также коэффициента деления потока θ1 обеспечит величи-

ны концентраций в выходных потоках, которые будут ближе всего к заданным.

Например, для идеального каскада типа IV при q = 1,59 и cF = 0,71%, cP = 4,4% , а также N = 96, f = 3 получены сле-

дующие значения параметров (табл. 1.2) [19]. Величина концентрации ценного компонента в отвале при этом получается равной 0,44%.

Таблица 1.2

Параметры ступеней идеального каскада

								Номер	Ls*/P	θ	s	c	s	c′,%	c′′,%	δU	s	/ P	δU	s	/ L 102
								ступени						s	s						s
1									1,40	0,120		0,45		0,706	0,44	0,0207			0,148
	2								75,51	0,981		0,71		0,71	0,45	1,2935				1,71
		3*							76,39	0,118		0,71		1,12	0,71	1,1329				1,48
			4						43,22	0,982		1,12		1,13	0,71	0,7390				1,71
				5					42,82	0,118		1,13		1,78	1,12	0,6364				1,48
					6				21,97	0,982		1,78		1,79	1,13	0,3748				1,70
						7			21,72	0,118		1,79		2,80	1,78	0,2341				1,49
							8		8,56	0,982		2,80		2,82	1,79	0,1451				1,70
								9	8,40	0,119		2,82		4,40	2,80	0,1261				1,50

*Точка подачи внешнего питания.

67

В рассмотренном примере в идеальном каскаде из несимметричных разделительных элементов коэффициент деления потока и удельная разделительная способность пилообразно меняются от ступени к ступени. Нечетные ступени в каскаде имеют значения θs = 0,118 и δU s /L*s =1, 48 10–2, а четные –

θs = 0,981−0,982 и δU s /L*s =1, 71 10–2. Относительный сум-

марный поток в таком каскаде равен ∑L*s /P = 299,99, а сум-

s

ма относительных разделительных способностей (мощностей) всех ступеней каскада, то есть разделительная способ-

ность каскада в целом равна ∑δU s /P = 4,793. Среднее зна-

s

чение разделительной способности δU s /L*s ступени состав-

ляет 1,58 10–2.

В идеальном каскаде из симметричных ступеней суммарный поток может быть рассчитан с помощью простого анали-

тического выражения. С учетом равенства α = β = q , а так-

же формул (1.7), (1.9) соотношения (1.107) – (1.109) могут быть переписаны в виде:

θ	s	=	1+(α −1)cs	,
			α +1

*		α +1		(cP −cs)
Ls	=	α −1	P
				c	(1	−c	)
				s		s

– для обогатительной части каскада;

*		α +1	(cs −cw)
Ls	=	α −1W
			c	(1	−c	)
			s		s

(1.150)

(1.151)

(1.152)

– для обеднительной части каскада.

Формулы (1.151) и (1.152) описывают дискретные распределения потоков по ступеням идеального каскада из симметричных ступеней. Величина потока на ступени с номером

68

(s = f ) имеет максимальное значение. В обогатительной час-

ти поток питания ступеней уменьшается в направлении отбора каскада, а в обеднительной части – в сторону отвала.

В соответствии с формулами (1.141) – (1.142), относительные концентрации ценного изотопа в отборе и в отвале связаны с числом ступеней в обогатительной и обеднительной частях каскада соотношениями (1.147). Следовательно, степень разделения каскада при заданных величинах N и f равна:

	Rp	=α N +1 = q	N +1
			2	.	(1.153)
	Rw

В соответствии с (1.153), число ступеней в идеальном каскаде при выполнении условия α = β будет равно

	N	ид	=	2	ln	Rp		−1.	(1.154)
				ln q		R	w

Очевидно, что для достижения такой же степени разделения, как в безотборном режиме, в данном случае потребуется примерно вдвое больше ступеней.

Для нахождения суммарного потока все концентрации, входящие в (1.151) и (1.152), выразим через RF , N и f , имея

в

виду

(1.146)

и (1.147), а также очевидное соотношение

R

s

=

cs

. В результате формулы (1.151) и (1.152) приобре-

1

−cs

тут вид:

для обогатительной части каскада

*

α +1 1

f −s

f −N −1

s−N −1

L

=

Pc

p

α

−α

+ R

F

(1−α

) ;

(1.155)

s

α −1 RF

для обеднительной части каскада

*

α

+1 1

f

f −s

s

Ls

=

Wcw α

−α

+ RF (α

−1) .

(1.156)

α

−1 RF

69

При суммировании L*	по ступеням каскада учтем, что для
s
m			N − f +1 и f
любого m ≥ 0 ∑α s = α m+1 −1		, а параметры
s=0	α −1

связаны с относительными концентрациями Rp , RF , и Rw

соотношениями (1.147). Принимая это во внимание, получим: для обогатительной части каскада

N

α

+1

1

R

p

*

∑Ls

= P

(2cp

−1) ln

+

α

−1 ln α

R

s= f

F

(1.157)

(c

−c

) α

(1−c

) −c

p

F

F

+

F

,

(α

−1)cF (1−CF )

для обеднительной части каскада

f −1

+1

1

R

*

α

w

∑Ls

=W

(2cw

−1) ln

+

−1 ln α

R

s=1

α

F

(1.158)

(c

−c

) α(1−c

) −c

w

F

F

+

F

.

(α

−1)cF (1−CF )

Суммируя (1.157) и (1.158) с учетом (1.77) и (1.78), полу-

чим

N

*

α +1

cp

∑Ls

=

P(2cp

−1)ln

+

(α −1)lnα

1

−cp

s=1

(1.159)

+W (2cw

−1)ln

cw

−F(2cF

−1)ln

cF

.

1

−cw

1−cF

Если разделить левую и правую части (1.159) на первый множитель в правой части, то получим

70