Загребаев Методы обработки статистической информации в задачах контроля 2008

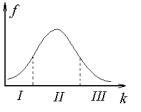
H1 : альтернативное предположение

2. Формируется некоторая функция k = fn (X1, ..., Xn ) от результатов наблюдения. Эта функция называется критерием. Так как величины X1 , …, Xn – случайные, то k является случайной величиной. Обязательным является, чтобы закон распределения f (k) был хорошо изучен и затабулирован в предположении справедли-

вости H0 .

Принцип построения критерия k: величиной критерия опре-

деляется мера расхождения имеющихся в распоряжении выборочных данных с высказанной гипотезой H0 .

3. Задается величина уровня значимости α. Величина априорного значения α зависит от тех потерь, которые мы понесем, отвергнув правильную гипотезу. Чем больше потери, тем меньше величина α. Обычно значения α выбираются из следующего ряда:

0,1	0,05	0,025	0,005	0,001.
4. Из таблиц, где затабулирована			f (k)	– плотность распределе-

ния k, при заданном уровне значимости находим точки, разделяющие всю область мыслимых значений k в зависимости от выбранной альтернативной гипотезы на три или две части (рис. 1.23).

Рис. 1.23. Плотность распределения критерия при справедливости нулевой гипотезы

(I – область неправдоподобно малых значений k; II – область правдоподобных значений k;

III– область неправдоподобно больших значений k)

5.В функцию k = fn (x1, ..., xn ) подставляем выборочные значения x1, ..., xn . Если окажется, что число k = fn (x1, ..., xn ) попадает во вторую область, то считают, что гипотеза H0 не противоречит

экспериментальным данным. Если же в первую или третью область, то, скорее всего, случайная величина k не подчиняется из-

81

вестному закону f (k) и это несоответствие объясняется неверностью гипотезы H0 , и мы от нее отказываемся.

Критические области. Мощность критерия

Критическая область – совокупность значений критерия, при котором отвергается гипотеза H0 .

Мощность критерия – вероятность принятия альтернативной гипотезы H1 , если она верна, или вероятность попадания критерия

в критическую область при условии правильности гипотезы H1 , т.е. мощность критерия – вероятность того, что H0 отвергнута, если H1 верна. Если β – вероятность совершить ошибку второго ро-

да, т.е. события «принята нулевая гипотеза, причем справедлива конкурирующая», то мощность критерия 1 −β .

Таким образом, чем больше мощность критерия, тем меньше вероятность совершить ошибку второго рода.

Проверка гипотезы о равенстве центров распределения двух нормальных генеральных совокупностей при известном σ

Пусть две случайные величины X и Y подчинены нормальному закону. Имеется две независимые выборки n и m. Необходимо проверить нулевую гипотезу о том, что статистическое ожидание этих двух генеральных совокупностей совпадают относительно альтернативной гипотезы – математические ожидания не равны.

В соответствии с общей логической схемой статистической проверки статистических гипотез, реализуем следующие шаги.

1. Выдвигаем гипотезу H0 и альтернативную ей гипотезу H1 .

H0 : M [X ] = M [Y ] .

H1 : M[X ] − M[Y ] > 0 .

2. Задаемся критерием проверки выдвинутой гипотезы H0 :

n

X

−Y

1

1

m

Z =

, где

X =

∑Xi , Y =

∑Yi .

n

m

σ X −Y

i=1

i=1

82

Ясно, что M X = M [X ],

иY распределены нормально. Понятно, что

M Y			= M [Y ], причем величины X

D[X ] D[Y ]

σ X

−Y

=

D X −Y

=

D X

+ D Y

=

+

.

n

m

Если справедлива H

, т.е. если

= M

,

то величина Z

0

M Y

Y

распределена по нормальному закону с параметрами: M [Z ]= 0 и

	σ[Z ]=1, т.е. f (Z) =	1	l−	Z 2
				2	.
		2π

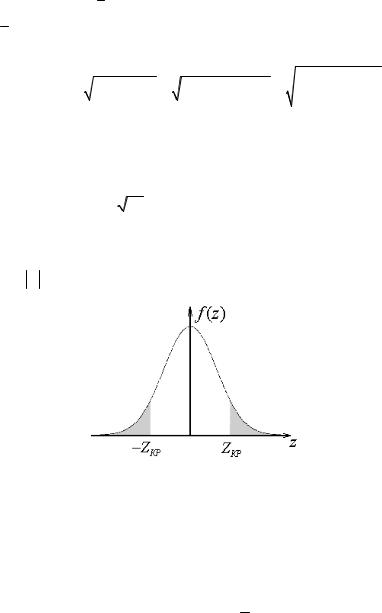
3. Задаемся величиной уровня значимости α, т.е. вероятностью отвергнуть истинную гипотезу, если она верна, что в геометрическом плане означает попасть в критическую область

α = P( Z > Zk ) (рис. 1.24).

Рис. 1.24. Иллюстрация к проверке гипотезы о равенстве центров распределения двух генеральных совокупностей

4. Из таблиц, где затабулирована f (z) – плотность распределе-

ния z, находим точки, разделяющие всю область мыслимых значений критерия на три части.

В силу симметрии нормального закона распределения имеем

P(0 < Z < Zk ) = 12 .

83

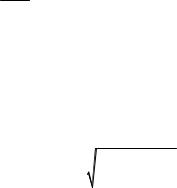
Эта вероятность есть сумма вероятности того, что случайная величина Z попадет в области 0 < Z < Zk и Zk < Z < ∞ , т.е.

12 = P(0 < Z < Zk ) + P(Zk < Z < ∞) .

С другой стороны, это соотношение можно записать, используя функцию Лапласа, определяющую вероятность попадания нормированной случайной величины Z в интервал (0 < Z < Zk ) :

12 = P(0 < Z < Zk ) + P(Zk < Z < ∞) = Φ(Zk ) + α2 ,

откуда Φ(Zk ) = 1−2α . Обратным интерполированием по таблицам функции Лапласа определяем величину Zk , т.е. критическую об-

ласть		−1		1− α
	Zk = Φ				.
				2

5. По экспериментальным данным вычислим:

1			n		1 m
		∑xi −					∑yi
Zэксп =	n i=1				m i=1				.
			D[x]	+		D[y]
			n
							m

Если Zнабл попадает в критическую область, то гипотезу о равенстве центров распределения следует отвергнуть. В противном случае можем сказать, что H0 не противоречит имеющимся экспе-

риментальным данным.

Рассмотрим случай, когда выдвигается другая альтернативная гипотеза.

1.H0 : M [X ]= M [Y ], H1 : M [X ]> M [Y ].

2. Критерий выберем тот же самый: Z =	X			−Y						.
	σ X				−Y

84

3.

Выбор альтернативной гипотезы определяет форму матема-

тической записи P(Z − Zk ) = α .

4.

Выбор критической области при этом находится из условия

P(0 < Z < Z

k

) + P(Z

k

< Z < ∞) =

1

2

или

1 = P(0 < Z < Zk ) + P(Zk < Z < ∞) = Φ(Zk ) + α ,

2

Φ(Zk ) =

1− 2α

, тогда Zk = Φ

−1

1− 2α

откуда получим

.

2

2

5.

Если Zэксп

=

X

−Y

> Zk , то H0 отвергаем.

σ X

−Y

Проверка гипотезы о равенстве центров распределения двух нормальных генеральных совокупностей

при неизвестном, но одинаковым σ

Пусть X и Y подчинены нормальному закону. Будем считать, что дисперсии этих случайных величин неизвестны, но одинаковы

σ2x = σ2y = σ2 . Пусть n и m – объемы выборок из генеральных сово-

купностей X и Y соответственно. Необходимо проверить нулевую гипотезу о равенстве математических ожиданий:

H0 : M [X ] = M [Y ]

относительно альтернативной

H1 : M [X ] ≠ M [Y ] ,

			1	n			1	m
X =				∑Xi , Y =				∑Yi .
			n i=1				m i=1

В качестве оценки для дисперсии выберем несмещенную оцен-

ку:

		1	n			1	m
	Sx2 =		∑(Xi − X		)2 , Sy2 =		∑(Yi −Y		)2 .
		n −1i=1				m −1i=1

85

Так как по условию σ2x = σ2y = σ2 , то для оценки σ2 целесооб-

разно использовать эту информацию и в качестве оценки дисперсии взять взвешенное значение от обеих выборок:

S2 =

Sx2 (n −1) + Sy2 (m −1)

.

n + m − 2

Если гипотеза

H0 справедлива, то случайная величина

X

−Y

подчинена нормальному

закону

с параметрами

] = 0 ,

M[X

−Y

2

1

1

D[X −Y ] = σ

+

.

n

m

Действительно,

M[X

−Y ] = M[X ] − M[Y ] = 0 ,

D[X]

D[Y]

1

1

2

1

1

D[X −Y ] = D[X ]+ D[Y ] =

+

= D

+

=σ

+

,

n

m

n

m

n

m

величина σ2 неизвестна. Понятно, что в этом случае оценка дисперсии разности средних значений может быть выражена формулой:

2

1

1

2

1

1

Sx2 (n −1) + Sy2 (m −1)

SX

=

+

S

=

+

.

−Y

n + m − 2

n

m

n

m

При этом легко показать, что

2

2

1

1

M[SX

]

= σ

+

= D[X −Y ].

−Y

m

n

Известно, что, если величина

подчинена нормальному

X

−Y

закону, то статистика

=

t =

X

−Y

X

−Y

SX

1

1 Sx2 (n −1) + Sy2 (m −1)

−Y

+

n + m − 2

n

m

подчиняется распределению Стьюдента с числом степеней свободы k = n + m − 2 .

86

При заданном α по таблицам функции Стьюдента находим tкр , такое, что P( t > tкр) = α . Далее вычисляем по экспериментальным

данным T =	x − y		nm(n + m − 2)	, и если его мо-
эксп	(n −1)sx2 + (m −1)s2y		n + m

дуль больше tкр , то гипотеза H0 отвергается, в противном случае она принимается.

Сравнение двух дисперсий нормальных генеральных совокупностей

Пусть генеральные совокупности X и Y распределены нормально и по независимым выборкам из этих совокупностей, соответственно, объемом n и m получены исправленные выборочные дис-

персии sx и sY . Понятно, что в силу ограниченности выборок зна-

чения этих величин могут не совпадать, даже если дисперсии генеральных совокупностей одинаковы. Возникает вопрос: случайно это расхождение, значимо ли оно? Иначе говоря, требуется при заданном уровне значимости α проверить нулевую гипотезу о том, что дисперсии генеральных совокупностей совпадают.

		1	n			1	m
	Так как Sx2 =		∑( Xi − X		)2 и Sy2 =		∑(Yi −Y		)2 являются,
		n −1 i=1				m −1 i=1

соответственно, несмещенными оценками дисперсий генеральных совокупностей X и Y, то выполняются соотношения:

M[S2	] = D	X	и M[S2	] = D .
X			Y	Y

Тогда нулевую гипотезу о равенстве дисперсий генеральных совокупностей X и Y можно записать следующим образом:

H0 : M[SX2 ] = M[SY2 ] ,

или

H0 : DX = DY .

Вкачестве критерия в данном случае выбирают отношение

большей дисперсии к меньшей F = Sб2 . Показано, что при спра-

Sм2

87

ведливости нулевой гипотезы величина F подчиняется распределе-
нию Фишера		–	Снедекора			со степенями				свободы k1 = n1 −1 и
k2 = n2 −1. При этом n1				– объем выборки, по которой вычислена
большая исправленная дисперсия, а n2 – меньшая. Оказывается,
что распределение Фишера – Снедекора зависит только от числа
степеней свободы k1 и k2				и не зависит от других параметров.
Распределение Фишера – Снедекора. Если U и V – независи-
мые случайные величины,					распределенные по закону χ2						со степе-
нями свободы k1 и k2 , то величина
						U / k1					(1.3.1)
						F = V / k2
имеет распределение, называемое F-распределением, или распре-
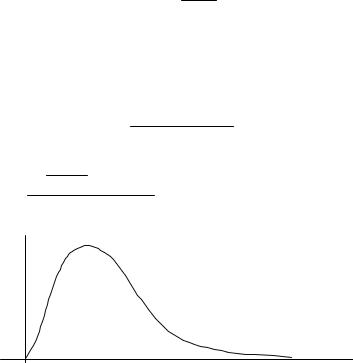
делением Фишера – Снедекора (рис. 1.25). Плотность распределе-
ния Фишера – Снедекора определяется выражением:
			0							при x ≤ 0;
						x(k1−2)/2					(1.3.2)
		f (x) =
			C0	(k		+ k x)	(k +k	2	)/2	при x > 0,
					2		1
						1
Г	k1	+ k2 kk1/2kk2 /2
		2	1	2
где C =						; Γ – гамма функция.
0	Г(k1 /2)Г(k2 /2)
f ( x)
										x
Рис. 1.25. Плотность распределения Фишера – Снедекора

88

Критическая область строится, исходя из вида конкурирующей гипотезы.

Рассмотрим пример. Пусть

H1 : D[ X ] > D[Y ] .

Необходимо вычислить отношение большей исправленной дисперсии к меньшей, т.е.

Fэксп = sб2 .

sм2

Затем по таблице критических точек распределения Фишера – Снедекора по заданному уровню значимости α и числам степеней свободы k1 и k2 ( k1 – число степеней свободы большей исправ-

ленной дисперсии) найти критическую точку Fкр , исходя из усло-

вия:

P(F > Fкр) = α .

Если Fэксп > Fкр , то гипотезу H0 отвергаем.

При данной конкурирующей гипотезе критическая область – односторонняя.

Проверка гипотезы о законе распределения. Критерий Пирсона

Ранее рассматривались способы проверки гипотез о различных параметрах закона распределения, причем сам закон распределения считался известным. Однако во многих задачах именно сам закон распределения неизвестен, и предположение о его виде является гипотезой, требующей проверки. Пусть высказывается предположение, что ряд наблюдений X1, ..., Xn образует случайную выбор-

ку, извлеченную из генеральной совокупности, имеющей плотность распределения вида f (x; θ1, ..., θs ) , где параметры θ1, ..., θs неизвестны. В этом случае для проверки гипотезы о том, что плотность распределения случайной величины X есть f (x; θ1, ..., θs ) ,

применяется критерий Пирсона.

Критерий Пирсона. Суть состоит в том, что сравниваются эмпирические и теоретические (в предположении справедливости ги-

89

потезы H0 : f = f (x; θ1, ..., θs ) ) частоты. Например, получены следующие данные:

	Эмпирические	6	13	38	74	106	85	30	10	4
	частоты
	Теоретические	3	14	42	82	99	76	37	11	2
	частоты

Возникает вопрос: случайно ли расхождение частот? С одной стороны, расхождение частот может быть случайным и объясняется малым числом измерений и ошибками при измерении. С другой стороны, возможно, что закон распределения, который мы выбрали для описания случайной величины и на основании которого рассчитаны теоретические частоты, не соответствует действительности. На эти вопросы и отвечает критерий распределения Пирсона. Для применения критерия Пирсона сделаем следующие шаги.

1. Разобьем область изменения случайной величины X на l интервалов 1, ..., l и подсчитаем по экспериментальным данным количество попаданий случайной величины в каждый из этих интервалов mi . При этом обычно разбиение на интервалы подчиняет

следующим условиям:

общее количество интервалов l должно быть не менее восьми (предполагается, что число неизвестных параметров распределения s не превосходит семи (на практике s ≤ 3 ));

в каждый интервал группировки должно попасть не менее 7 – 10 выборочных значений xi .

2. На основании выборочных данных x1, ..., xn строятся оценки

неизвестных параметров θ1*, ..., θ*s .

3. Вычислим вероятности событий, что значение случайной ве-

личины X попадет в		i	интервал:
P = F		(x ; θ*, ..., θ* ) − F				(x	; θ*, ..., θ* ) ,
i	M	i	1	s	M	i−1	1	s
где xi и xi−1 – правый и левый концы интервала								i .

90