Загребаев Методы обработки статистической информации в задачах контроля 2008

			1	n			1		D
D[Xв] =				D ∑M[Xi ]		=		nD[X ] =	x	. (1.2.19)
			n2				n2
				i=1					n

Сформируем случайную величину, равную отношению

Xв − mx . Если σx – известная величина, то сформированная ве- (σx / n)

личина также подчиняется нормальному закону распределения с параметрами

− m

1

X

в

x

] = 0 ,

M

=

M [X

в

− m

x

(σ

/

(σ

x

/ n)

x

n)

− m

1

n

X

в

x

1 .

D

=

D[X

в

] =

D

x

=

/

(σ2

/

n)

σ2n

(σ

x

n)

x

x

Однако дисперсия генеральной совокупности σ2x почти никогда

не известна. Поэтому практический интерес представляет собой распределение статистики:

в − mx

t =

X

n ,

(1.2.20)

S

n

)2

S2

n (X

− X

в

где

=

i∑=1

i

– исправленная выборочная дисперсия

n −1

n

в гипотетическом варианте.

Можно показать, что функция плотности распределения статистики t зависит только от объема выборки n и при n → ∞ стремится к функции плотности распределения нормального закона

(рис. 1.19).

Рис. 1.19. Распределение Стъюдента при различном объеме выборки

71

Распределение Пирсона. Рассмотрим n одинаково распределенных величин X1, ..., Xn c нулевым математическим ожиданием и единичной дисперсией

( M[X1] =... = M[Xn ] = 0; D[X1] =... = D[Xn ] =1)
и функцию от них:
χ2 = X12 +... + Xn2 .	(1.2.21)

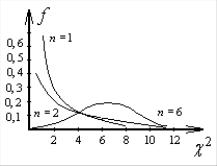
Плотность распределения случайной величины χ2 носит назва-

ние «распределение Пирсона» или « χ2 распределение». На

рис. 1.20 показано распределение Пирсона для различного объема выборки n. Можно показать, что при n → ∞ распределение асим-

птотически нормальное с центром в точке χ2 = n и дисперсией 2n.

Рис. 1.20. Распределение Пирсона

При n → ∞ распределение асимптотически нормальное с цен-

тром в точке χ2 = n и дисперсией 2n.

Легко

показать,

что исправленная выборочная

дисперсия

n

)2

S2

n (X

− X

связана с величиной χ2 соотношением

=

i∑=1

i в

n −1

n

χ2 =

S2 (n −1)

.

(1.2.22)

σ2

x

72

Доверительный интервал для математического ожидания и дисперсии

Существует два подхода к построению доверительных интервалов при нахождении оценок параметров. Первый из них приводит к построению «точных» доверительных интервалов и основан на переходе от закона распределения оценки θ* , которая зависит от самого неизвестного параметра θ, к какой-нибудь другой функции от наблюдаемых величин X1, ..., Xn , которая уже не зависит от неиз-

вестных параметров. Второй способ – приближенный. Продемонстрируем применение этих подходов на следующих примерах.

Пусть получена выборка x1, ..., xn из нормальной генеральной

совокупности с неизвестными параметрами mx						и	Dx .			По этим
										n
									∑xi2
данным		получены		оценки	параметров	x		=	i=1		и
						в				n
	n
s2 =	∑(xi − xв)2
	i=1		. Требуется построить доверительный							интервал
		n −1

для оценок этих параметров.

Доверительный интервал для математического ожидания. В

соответствии с постановкой задачи необходимо найти такое , чтобы выполнялось соотношение P( xв − mx < ) = β , т.е. найти такой

доверительный интервал около среднего выборочного, который с заданной вероятностью β «накрывал» бы истинное значение мате-

матического ожидания. Умножим неравенство

xв − mx

<

на по-

ложительную величину

n

, тогда получим

n

x

− m

x

<

.

s2

s2

в

s2

n

Обозначив t =

n(xв − mx )

, получим

t

<

.

s

s

2

n

73

Таким образом, исходная постановка	задачи трансформирова-
лась в следующую: найти такое , чтобы	с заданной вероятностью

β выполнялось неравенство

t

< tβ , где tβ =

, т.е. выполнялось

s2

n

равенство P(

t

< tβ) =β.

В этом соотношении t – статистика, подчиненная закону Стьюдента, т.е. случайная величина с известной плотностью распределения f (t) . С учетом четности функции плотности распределения

f (t) , условие P( t < tβ) =β равносильно следующему:

tβ

β = 2 ∫ f (t)dt .

0

По таблице Стьюдента (см. пример 1.5) зависимости tβ от числа степеней свободы k = n −1 и заданной вероятности β находим tβ , а затем :

= t	s2	.
β	n

Пример 1.5. Пусть произведено пять независимых опытов со случайной величиной X, распределенной нормально с неизвестными параметрами mx и σx . Результаты опытов приведены в табли-

це:

х1	х2	х3	х4	х5
–2,5	3,4	-2,0	1,0	2,1

Найти оценку математического ожидания и построить вокруг него 90 % доверительный интервал, т.е. доверительный интервал, соответствующий вероятности β = 0,9:

	n
m* =	∑xi			1	n
	i=1	= 0, 4 ;	s2 =		∑(xi − m* )2 = 6, 445 .
	n
				n −1i=1

74

Число степеней свободы k = n −1 = 4 . По таблице Стьюдента

tβ			β
1	0,1	0,2	0,3	…	0,9
2
3
4					2,13
5

для данного числа степеней свободы и доверительной вероятности

определяем	t = 2,13	и величину	= t	s2	= 2,42 , следовательно,
	β		β	n

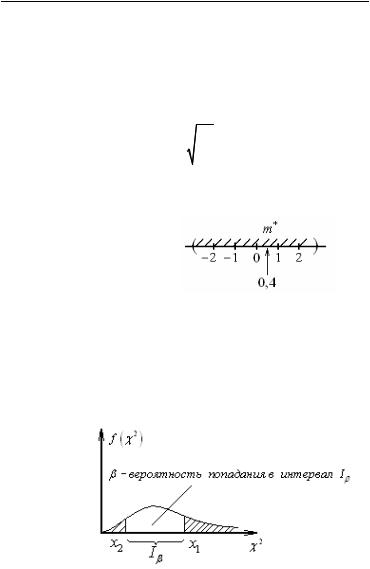
истинное значение математического ожидания с вероятностью

90 % находится в интервале (–2,02; 2,82) (рис. 1.21).

Рис. 1.21. Интервальное оценивание математического ожидания

Доверительный интервал для дисперсии. Несмещенной оцен-

				1	n
	кой дисперсии является величина s2 =				∑(xi − xв)2 . Известно,
				n −1i=1
	что величина	1	(n −1)s2 = χ2 подчинена закону χ2 .
		σ2
		x

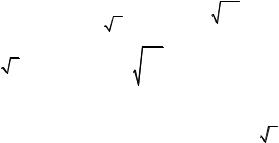
Рис. 1.22. Расположение доверительного интервала

75

На рис. 1.22 показана функция плотности распределения с указанием расположения интервала Iβ . Интервал Iβ можно выбрать

так, чтобы вероятность уклонения случайной величины χ2 влево и вправо за интервал была одинаковой и равна величине α2 = 1−2β ,

где β – доверительная вероятность. Действительно, так как функция плотности распределения f (χ2 ) при заданном числе степеней

свободы k = n −1 известна,	то вероятность того, что случайная ве-
личина χ2 выйдет за правую границу интервала χ2		есть площадь
под кривой	1
+∞	f (χ2 )dχ2 = α .	(1.2.23)
∫
χ2	2
1

Вероятность того, что случайная величина χ2 будет правее точ-

ки χ12 , есть площадь под кривой правее точки χ12 . Эту площадь

можно определить следующим образом. Из всей площади под кривой (которая равна единице) вычесть площадь под кривой между

точками 0 и χ22 , которая равна α2 , т.е. 1− α2 . Таким образом, левая граница интервала Iβ находится из решения уравнения

+∞	f (χ2 )dχ2 =1−	α .
∫			(1.2.24)
χ22		2

Решение уравнений (1.2.23) и (1.2.24) возможно либо численно,

	либо уже затабулировано в соответствующих таблицах.
	Теперь считая χ2			и χ2 известными, найдем по I			β	искомый ин-
	1			2
	тервал для оценки дисперсии,				который накрывает точку				σ2x (ис-
	тинное значение) с вероятностью β. Из условия P(χ2							< χ2	< χ2 ) = β
		1			1	2			1
	следует, что		(n −1)s2 < χ2 и			(n −1)s2 > χ2 . Это означает, что
		σ2		1	σ2	2
		x			x

76

	1	(n −1)s2 < σ2	<	1	(n −1)s2 .
	χ2			χ2
		x
	1			2

Таким образом, получен доверительный интервал для оценки дисперсии, внутри которого лежит истинное значение дисперсии с заданной доверительной вероятностью, т.е.

		1	(n −1)s2 < D			1	(n −1)s2
	P			x	<				=β.	(1.2.25)
		χ2				χ2
		1				2

Приближенное определение доверительных интервалов. В

основе подхода к приближенному определению доверительных интервалов лежит возможность применения предельных теорем теории вероятности при достаточно больших объемах выборки. Например, как установлено практикой, при объеме выборки n > 20 закон распределения суммы случайных величин можно считать нормальным. Рассмотрим несколько примеров приближенного определения доверительных интервалов.

Пример построения доверительного интервала для математического ожидания и дисперсии

Пусть имеется выборка x1, ..., xn , причем математическое ожидание и дисперсия неизвестны. Для них получены оценки:

	1	n			1	n
m* =		∑xi ,	s2	=		∑(xi − m* )2 .
	n i=1				n −1i=1
Построим доверительный			интервал Iβ для математического

ожидания при заданной вероятности β. Воспользуемся тем, что

m* – сумма независимых случайных величин с одним и тем же законом распределения. Тогда, согласно предельной теореме, закон распределения суммы можно считать нормальным при n → ∞ . Предположим, что и при данном, конкретном, конечном n сумма

n

∑xi будет подчинена нормальному закону распределения. Следо-

i=1

77

вательно, оценка m* =	1 n	также будет подчинена нормальному
	∑xi
	n i=1
закону с математическим ожиданием m			x	и дисперсией					D =	Dx	.
									x	n
Предположим, что Dx
	известна и найдем такую величину , для
которой будет выполняться		неравенство		P(		m* − m		<	) = β. Так

как закон распределения оценки m* – нормальный, то эту вероятность можно выразить через функцию Лапласа, т.е.

P(

m* − m

D .

<

) = Φ

,

где

σ

x

=

σx

2

x

Тогда = Φ−1(β) 2σx ,

Dx

причем

σx =

определяется тоже по

n

данным выборки.

Таким образом, доверительный интервал для математического ожидания есть Iβ = (m* − , m* + ) , где величина Φ−1(β) 2 зата-

булирована в таблицах или находится численно.

Пример построения приближенного доверительного интервала для дисперсии

		1			n
Оценка дисперсии	s2 =				∑(xi − m* )2 представляет собой
		n −
			1i=1
	(x − m* )2
сумму величин вида:	i			. Эти величины не являются неза-
	n −1

висимыми, так как в любую из них входит оценка математического

ожидания m* . Однако при достаточно большом n закон распределения суммы приближается к нормальному. Предположим, что это так, и найдем характеристики этого закона. Так как оценка дисперсии является несмещенной, то выполняется соотношение

M [S 2 ] = Dx .

78

	Можно показать, что
	D[S 2 ] =	1	μ4 −	n − 3	Dx2 ,	(1.2.26)
		n		n(n −1)
	+∞
	где μ4 = ∫ (x − mx )4 f (x)dx – четвертый момент случайной вели-
	−∞
	чины X.

Заменим в выражении (1.2.26) истинные значения Dx и μ4 их оценками, полученными по конечной выборке объема n:

s2 =

1

n

− m* )2 ,

∑(xi

n −1i=1

n

μ*4

∑(xi − m* )4

=

i=1

.

n

Можно показать, что D[s2 ] =

2

s2 , откуда σD = s

2

.

n −1

n −1

Затем доверительный интервал Iβ = (s2 −

, s2 + )

строится так

же, как для математического ожидания, где

= Φ−1(β)

2σD .

1.3. Статистическая проверка статистических гипотез

Статистическая гипотеза – предположение относительно вида закона распределения или величины неизвестных параметров известного закона распределения [1, 3].

Выдвинутая гипотеза называется нулевой и обозначается H0 . Наряду с этой гипотезой рассматривают конкурирующую или альтернативную ей гипотезу H1 .

Если исследуются параметры известного распределения, то в этом случае постановка задачи может выглядеть, например, так:

H0 : M[X ] =1 (математическое ожидание случайной величины X равно 1);

79

H1 : M[X ] ≠1 (математическое ожидание случайной величины

X не равно 1).

Цель статистической проверки статистических гипотез – установления факта: не противоречит ли выдвинутая гипотеза имеющимся выборочным данным x1, ..., xn .

Статистическая проверка гипотез – процедура обоснованного сопоставления (с помощью того или иного критерия) высказанной гипотезы H0 и экспериментальных выборочных данных.

При проверке выдвинутой гипотезы возможны ошибки двух видов – ошибки первого и второго рода.

Ошибка первого рода – непринятие верной статистической гипотезы.

Ошибка второго рода – принятие неверной статистической гипотезы.

Для наглядности в табл. 1.2 показаны введенные выше определения ошибок при проверке гипотез.

		Таблица 1.2
Виды ошибок при проверке статистических гипотез
		Неверна
Гипотеза H0	Верна
Отвергается	Ошибка 1-го рода	Правильное решение
Принимается	Правильное решение	Ошибка 2-го рода

Из табл. 1.2 видно, что ошибка первого рода – когда отвергается истина, а ошибка второго рода – когда принимается ложь.

Неотрицательный результат статистической проверки статистических гипотез не означает, что высказанное предположение абсолютно верно, просто оно не противоречит выборочным данным – так и необходимо рассматривать результат проверки гипотезы H0 .

Вероятность совершить ошибку первого рода обозначают α и называют уровнем значимости, а вероятность совершить ошибку второго рода обозначают β.

Общая логическая схема проверки статистических гипотез.

1. Формулируется нулевая и альтернативная гипотезы. H0 : предположение.

80