
Лабораторный практикум по физике для вечернего фак 2007
.pdfФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
МОСКОВСКИЙ ИНЖЕНЕРНО-ФИЗИЧЕСКИЙ ИНСТИТУТ (ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ)
ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО ФИЗИКЕ
ДЛЯ СТУДЕНТОВ ВЕЧЕРНЕГО ФАКУЛЬТЕТА МИФИ
Рекомендовано УМО «Ядерные физика и технологии» в качестве учебного пособия
для студентов высших учебных заведений
Москва 2007

УДК 53(076.5) ББК 22.3Я7 Л12
Лабораторный практикум по физике для студентов вечернего факультета МИФИ. / В.В. Грушин, С.О. Елютин, Н.А. Добродеев, С.Л. Тимошенко, А.А. Богданов. – М.: МИФИ, 2007. – 212 с.
Лабораторный практикум содержит введение и описание 22 работ по разделам: «Электромагнитные колебания и волны», «Геометрическая и волновая оптика», «Излучение и спектры», «Элементы физической электроники».
Во введении описываются правила выполнения лабораторных работ и правила представления полученных результатов. В частности, правила построения экспериментальных графиков, правила математической обработки результатов, расчетов ошибок. Описания лабораторных работ состоят из теоретического введения, указаний по методике выполнения работы, образцов таблиц для записи полученных результатов измерений, формул для расчета определяемых величин и их погрешностей. В конце каждого описания сформулированы контрольные вопросы, а в конце каждого раздела указана учебная литература для самостоятельного изучения вопросов теории.
Лабораторный практикум предназначен для студентов вечернего факультета, выполняющих лабораторные работы по физике в лабораториях кафедры физики. Лабораторные работы, как правило, выполняются после изучения соответствующего раздела в теоретическом курсе.
Пособие подготовлено в рамках Инновационной образовательной программы.
Рецензент дɪфиз -мат. наук, проф А.И. Маймистов
ISBN 978-5-7262-0835-0
© Московский-инженерно физический институт (государственный университет), 2007
Работа напечатана по авторскому макету
Подписано в печать 16.11.2007. Формат 60×84 1/16. Объем 13,25 п.л. Уч.-изд.л. 11,5. Тираж 150 экз.
Изд. № 3/56 Заказ № 0-604 Московский инженерно-физический институт (государственный университет).
Типография издательства «Тровант», г. Троицк Московской обл.
СОДЕРЖАНИЕ
Введение ……………………………………………………………….5
Электромагнитные колебания и волны
Работа 1. Исследование гармонических колебаний с помощью электронного осциллографа………………………………………….20
Работа 2. Исследование колебаний в простом колебательном кон-
туре…………………………………………………………………….25
Работа 3. Изучение резонанса в электрическом колебательном кон-
туре………………………………………………….……………….…31
Работа 4. Измерение фаз и амплитуд в - цепи переменного тока ………………………………………………………………........36
Работа 5. Измерение коэффициента трансформации………...……42
Работа 6. Определение длины волны и скорости звука в возду-
хе…………………………………………………………………..….. 47 Литература………….………………………………………………..52
Элементы Физической электроники
Работа 7. Компаратор…………………………..……………………53
Работа 8. Усилитель на биполярном транзисторе………….……..63 Работа 9. Фурье-анализ периодических сигналов…………….….71
Литература…………………………………….……………………..89
Геометрическая и волновая оптика»
Работа 10. Определение показателя преломления света для жидко-
стей…………………………………………………………………….90
Работа 11. Определение фокусного расстояния собирающей и рассеивающий линз…….………….................................……….…96
Работа 12. Интерференция света в оптической схеме с бипризмой Френеля………………………………………….……104
Работа 13. Кольца Ньютона………………………………………..111 Работа 14. Дифракция света…………………………………….….118
Работа 15. Поляризация света………………………………….…..126
Работа 16. Рассеяние света в мутной среде……………………….136
Работа 17. Основы голографической интерферометрии диффузно-
отражающих объектов…………………………………..……….....147 Литература………………………………………………................162
3
Излучение и спектры
Работа 18. Внешний фотоэффект………………………………….164
Работа 19. Линейчатые спектры испускания……..……………….171 Работа20. Излучение газового лазера…………..………………….180
Работа21.Модуляция света…………………………...…………….189
Работа 22. Прохождение света сквозь халькогенидные пленки…197
Литература………………………………………………………... 212
4
ВВЕДЕНИЕ
Погрешности в физических измерениях
В экспериментальной науке нет точных измерений, все они обладают определенной погрешностью. Обычно результат измерения записывается в виде l ±σ , где l − измеренная величина, а σ ее стандартное отклонение или погрешность. Часто определить погрешность столь же важно, как и саму величину.
Измеренная величина может отличаться от истинного значения вследствие двух типов погрешностей: систематических и случайных погрешностей.
Систематические погрешности.
Они возникают из-за сбоев или дефектов аппаратуры, просчетов в выборе методики эксперимента; все повторяющиеся измерения содержат ту же погрешность. Например, калибровка вольтметра или секундомера может быть неправильной. Систематические ошибки могут быть выявлены только тщательной проверкой используемых приборов и методики проведения эксперимента. Важно оценить верхний предел всех оставшихся возможных систематических погрешностей, так они дают вклад в погрешность в конечном результате.
Случайные погрешности.
Эти погрешности являются следствием случайных отклонений в условиях работы измерительной аппаратуры, они могут возникать при снятии отсчетов или из-за статистической природы измеряемых величин. Типичное значение случайных погрешностей можно получить повторением измерения много раз.
Примеры случайных погрешностей:
•конечная точность, с которой масштаб или шкала может быть считана (можно считать эту точность в лучшем случае до 1/10 деления шкалы);
5
•трудности в считывании показаний прибора из-за движения или дрожания стрелки.
Косвенные погрешности.
Часто необходимо определить погрешность σ f величины f ,
где f = f (x, y...), а x, y... были измерены с погрешностями σx,σy .... Погрешность σ f вычисляется по формуле:
2 |
|
∂f 2 |
2 |
|
∂f |
2 |
2 |
+... |
(В.1) |
|
σ f |
= |
|
σx |
+ |
|
|
σy |
|||
|
|
∂x |
|
|
∂y |
|
|
|
|
|
Заметим, что для того чтобы уравнение (В.1) было справедливо, погрешности σx,σy ... должны быть независимы. К примеру, если
мы измерим l1 и l2 , а затем вычислим p = l1 +l2 и q = l1 −l2 , тогда p и q не являются независимыми. Уравнение (В.1) лучше всего
иллюстрируется некоторыми простыми примерами: предположим
f = ax2 (a = const ), тогда из уравнения (В.1): |
|
|
|||||||||
|
|
|
|
σ f |
= |
2σ |
x |
, |
|
|
|
|
|
|
|
|
f |
x |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
т.е. относительная |
погрешность |
Ex |
= σx удваивается. Предполо- |
||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
жим, что f |
= x + y |
или |
f = x − y , |
тогда σ 2f |
=σx2 +σy2 . |
Заметим, |
|||||
что погрешности складываются как квадраты |
и что σ f |
меньше, |
|||||||||
чем σx |
+σy . Например, |
если σx =σy |
=1 мм, |
тогда σ f =1, 4 мм. |
|||||||
Если |
σx |
значительно |
меньше |
чем |
σy , тогда σ f =σy . Если |
||||||
σx =1 мм, |
σy =10 мм, тогда σ f |
=10 мм. |
|
|
|||||||
Предположим, что |
f = xy или f |
= x |
y , тогда |
|
|
||||||
6

σ f |
2 |
|
σ |
|
2 |
|
σy 2 |
||
|
|
|
= |
|
x |
+ |
|
. |
|
f |
|
y |
|||||||
|
|
|
x |
|
|
|
|||
В этом случае уже относительные погрешности складываются как
квадраты величины: например, если |
σx =1% , |
σy |
=1% , тогда |
|
|||
|
x |
y |
|
σff =1, 4% . И вновь из-за того, что складываются квадраты вели-
чин, основной вклад в σ f дает величина с наибольшей погрешностью.
Многократные измерения.
Предположим, измеряем величину х n- раз и получаем результаты измерений x1, x2 ,...xn и предположим, что каждое измерение имеет
одну и ту же приборную погрешность σ1 (значение σ1 получено из
оценки надежности каждого измерения: класса точности прибора, цены деления, количества разрядов цифрового индикатора и т.п.). Естественно сформировать среднее значение
|
|
1 |
|
|
1 |
n |
|
x |
= |
|
(x1 + x2 +...) = |
∑xi . |
(В.2) |
||
n |
|
||||||
|
|
|
n i=1 |
|
|||
Так как величины x1, x2 ,... |
независимы, можно использовать урав- |
||||||
нение (В.1), положив |
x |
≡ f , x1 ≡ x, x2 |
≡ y и т.д., |
и получить |
|||
|
σ x |
=σ1 n , |
|
|
(В.3) |
||
что представляет собой погрешность в определении среднего значения.
Значения непосредственно измеренных величин разбросаны около среднего значения. Ясно, что величина разброса должна быть близка к погрешности одного измерения. Чтобы быть более точными, определим:
7
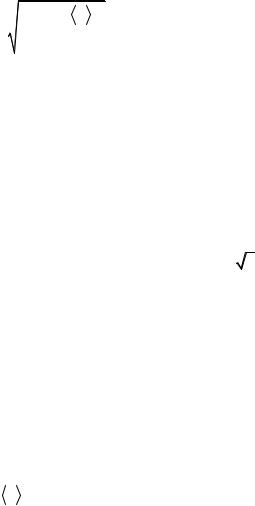
σ j = |
∑(xi |
− x )2 |
|
||
i |
|
|
(В.4) |
||
n − |
1 |
||||
|
|
||||
где σ j − величина разброса при снятии измерений; предполагаем σ j и σ1 приблизительно равными.
Если они не равны, тогда величина разброса результатов отличается от погрешностей σ1 в каждом акте считывания и, следовательно, неправильно интерпретируется величина случайной погрешности. Если σ j и σ1 приблизительно одинаковы, тогда можно использо-
вать либо σ j , либо σ1 .Таким образом, при многократном воспроизведении результатов измерений есть два преимущества:
• погрешность в определении среднего уменьшается как 1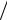 n ;
n ;
• можно сравнивать экспериментальную погрешность σ1 с разбросом измерений σ j и, таким образом, проверить наше понимание источника случайных ошибок.
Заметим, что:
• если n =1 , тогда σ j не определена, как и должно быть;
•если n ≤ 5 , оценка для σ j может быть не очень надежной.
Вэтом случае оценку измеренного значения и погрешности измерений следует проводить по приближенным формулам:
x = |
xmax + xmin |
; |
|
(В.5) |
||
|
|
|||||
|
2 |
|
|
|
||
σ j |
= |
xmax − xmin |
. |
(В.6) |
||
|
||||||
|
2 |
|
|
|
||
С одной стороны, случайные процессы влияют на отсчеты независимо. С другой стороны, систематические погрешности влияют
на погрешность отсчетов одинаковым образом. Так, разброс (σ j в
8
уравнении (В.4)) нескольких повторяющихся измерений определяется случайными эффектами, а не систематическими. К примеру, если истинное значение величины есть 8.424 и на точность измерений влияют случайные факторы, а не систематические , тогда серия измерений могла бы быть 8.6, 8.2, 8.3, 8.4, 8.4, давая среднее значе-
ние  x
x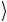 = 8, 40, σ j = 0, 20. Но если присутствуют только систематические эффекты, набор результатов мог бы быть 8.7, 8.7, 8.7, 8.7, 8.7, с
= 8, 40, σ j = 0, 20. Но если присутствуют только систематические эффекты, набор результатов мог бы быть 8.7, 8.7, 8.7, 8.7, 8.7, с 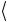 x
x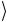 = 8.7 и без разброса. Следовательно, σ j должна оцени-
= 8.7 и без разброса. Следовательно, σ j должна оцени-
ваться с погрешностями, возникающими из только случайных эффектов.
После того как средняя величина вместе с погрешностями из-за случайных процессов подсчитана, нужно рассмотреть влияние систематических погрешностей. Например, несколько измерений с одним и тем же секундомером дают 224,3 ± 0,2 с. для среднего значения и ее погрешности. Но секундомер был сконструирован так, что он дает точность 1/1000 (т.е. 0,22 с. за 224 с). Таким образом, все измерения из-за систематических эффектов имеют погрешности порядка этой величины. Следовательно, 0.2 сек случайной погрешности должны быть объединены с 0,22 с. систематической погрешности (суммированы их квадраты), и тогда они дают результаты
224,3 ± 0,4 с.
Случайные искажения могут быть учтены при многократном повторении измерения при тех же условиях, но систематические искажения требуют анализа причин несовершенства приборов и методик измерения.
В заключение приведем формулы для вычисления относительных погрешностей Ef и абсолютных погрешностей σ f некото-
рых функций (табл. В.1 в конце введения).
9
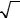
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица В.1 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Функция |
|
|
|
|
|
Абсолютная |
|
|
|
|
|
|
|
|
|
Относительная |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
погрешность |
|
|
|
|
|
|
|
|
|
погрешность |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
f = x + y |
|
|
|
= |
|
|
|
|
2 |
+ |
|
|
2 1/ 2 |
|
|
|
|
|
|
|
|
|
|
σ f |
|
|
|
|
|
σx +σy |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
σ f |
|
(σx |
σy ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
x |
|
+ y |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
f = x − y |
|
|
|
= |
|
|
|
|
2 |
+ |
|
|
2 1/ 2 |
|
|
|
|
|
|
|
|
|
|
σ f |
|
|
|
|
|
|
σx +σy |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
σ f |
|
(σx |
σy ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
x − y |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
f = xy |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 1/ 2 |
|
|
σf |
|
|
|
|
σ |
|
|
|
2 |
|
|
σy 2 1/2 |
|
||||||||||||||||||||||||||||
|
|
|
|
σ f |
|
= ((xσy ) |
|
|
+( yσx ) ) |
|
|
|
|
|
|
|
= |
|
|
x |
+ |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
x |
|
|
|
y |
|
|
|
|
|||||||||||||||||||||
f |
= xyz |
σ f |
|
= ((xyσz )2 +( yzσx )2 + |
σ f |
|
|
|
|
|
σ |
|
|
2 |
|
|
|
σy |
|
2 |
σ |
2 1/ 2 |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
1/ 2 |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
x |
|
|
+ |
|
|
|
|
|
+ |
|
z |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
+(xzσy ) |
) |
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
x |
|
|
|
|
|
y |
|
|
z |
|
|
||||||||||||||||||||||||||||||
|
f = |
x |
|
|
|
|
|
(( yσ |
|
)2 |
+(xσ |
|
)2 )1/ 2 |
|
|
|
σ f |
|
|
|
|
σ |
|
|
|
2 |
|
|
σy |
2 1/ 2 |
|
|
|||||||||||||||||||||||||||||||
|
y |
σ |
f |
|
= |
|
|
|
|
|
|
x |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
x |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
x |
|
|
|
|
y |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
f = xn |
|
|
|
|
|
|
|
|
|
|
= nx |
n−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ f |
|
|
|
|
|
|
|
|
|
σ x |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
σ f |
|
σx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
f = n x |
|
|
|
|
|
1 |
|
|
1 |
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ f |
|
= |
|
|
1 σx |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
σ f |
= |
|
|
|
|
xn |
|
σx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
n |
|
|
|
|
x |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
f |
= sin x |
σ f |
= cos x σx |
|
|
|
|
|
|
|
|
|
|
σ f |
= ctgx σx |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
f |
= cos x |
σ f |
= sin x σx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ f |
|
|
|
= tgx σx |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
f |
= tan x |
σ f |
= |
|
σx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ f |
|
|
|
= |
|
|
2σx |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
cos2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
sin 2x |
|
|
|
|
||||||||||||||||||||||||||||||
f |
= ctgx |
σ f |
= |
|
σx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ f |
|
|
= |
|
2σx |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
sin2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
sin 2x |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
f |
= ln x |
σ |
|
f |
= |
|
σ |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ f |
= |
|
|
σ |
x |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
x ln x |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
f = ex |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
σ f |
= e σx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=σx |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
10
