Ответы к государственному экзамену по физике (2006 г).
Материал предназначен исключительно для подготовки к государственному экзамену по физике 2006. Предполагается, что читатель уже имеет представление о соответствующих разделах физики. DEMO-версия: в некоторых вопросах приведены только указания к выводу формул и/или результат, также местами под знаком «+» даны рекомендации к построению более полного ответа.
Содержание. |
|
Механика....................................................................................................................................... |
3 |
1. Обобщенные координаты. Функция Лагранжа. Принцип наименьшего действия. ................ |
3 |
2.Законы сохранения импульса, момента импульса и энергии. Их связь с однородностью и
изотропностью пространства и однородностью времени................................................................... |
4 |
3. Движение в центральном поле. Интегралы движения. Уравнение траектории....................... |
5 |
4.Рассеяние частиц неподвижным силовым центром. Дифференциальное сечение рассеяния.
Формула Резерфорда. ............................................................................................................................. |
6 |
5.Малые колебания системы материальных точек. Свободные колебания. Затухающие
колебания................................................................................................................................................. |
8 |
6. Вынужденные колебания. Явление резонанса. ........................................................................... |
8 |
7.Кинематика и динамика твердого тела. Тензор инерции. Момент инерции. Уравнения
Эйлера. ..................................................................................................................................................... |
9 |
8. Функция Гамильтона. Уравнения Гамильтона. Канонические преобразования. .................. |
10 |
9.Преобразования Лоренца и их геометрическая интерпретация. Пространство Минковского. 11
Термодинамика. Молекулярная физика. Статистическая физика................................. |
13 |
||
10. |
Тепловая машина Карно. Коэффициент полезного действия.................................................. |
13 |
|
11. |
Термодинамическое и статистическое определение энтропии. Неравенство Клаузиуса. |
|
|
Второе начало термодинамики............................................................................................................ |
|
13 |
|
12. |
Равновесие фаз. Уравнение Клапейрона–Клаузиуса. |
............................................................... |
13 |
13. |
Явление переноса: диффузия и теплопроводность................................................................... |
|
14 |
14. |
Распределение молекул по скоростям........................................................................................ |
|
14 |
15. |
Канонический ансамбль. Статистическое определение свободной энергии. ........................ |
15 |
|
16. |
Свободная энергия идеального газа. Уравнение состояния и химический потенциал |
|
|
идеального газа. .................................................................................................................................... |
|
15 |
|
17. |
Флуктуации термодинамических величин. ............................................................................... |
|
16 |
18. |
Распределения Ферми–Дирака и Бозе–Эйнштейна. ................................................................. |
|
16 |
19. |
Уравнение Ланжевена. Формула Эйнштейна для среднего квадрата смещения броуновской |
||
частицы. ................................................................................................................................................. |
|
17 |
|
20. |
Уравнение Фоккера–Планка для распределения броуновских частиц по скоростям. .......... |
17 |
|
Электричество. Электродинамика. ....................................................................................... |
|
18 |
|
21. |
Теорема Гаусса и ее применение к вычислению электрических полей простейших |
|
|
распределений плотности заряда. ....................................................................................................... |
|
18 |
|
22. |
Теорема Стокса и ее применение к вычислению магнитных полей простейших |
|
|
распределений плотности тока............................................................................................................ |
|
18 |
|
23. |
Проводники и диэлектрики в электростатическом поле.......................................................... |
19 |
|
24. |
Система уравнений Максвелла для напряженности электрического и индукции магнитного |
||
полей в вакууме..................................................................................................................................... |
|
19 |
|
25. |
Уравнение непрерывности (закон сохранения заряда) в дифференциальной и интегральной |
||
формах.................................................................................................................................................... |
|
19 |
|
26. |
Выражения для напряженности электрического и индукции магнитного полей через |
|
|
скалярный и векторный потенциалы. Калибровочная инвариантность. ......................................... |
20 |
||
27. |
Ковариантная формулировка уравнений Максвелла и динамические уравнения для |
|
|
потенциалов........................................................................................................................................... |
|
21 |
|
GosPhys8 v7.02 Copyright © 2006 Davyd Tsurikov |
e-mail: DavydTsurikov@mail.ru |
1 |
|
28. |
Объемная плотность и поток энергии электромагнитного поля. |
...........................................21 |
29. |
Условия на границе раздела двух сред. ..................................................................................... |
21 |
Оптика. ........................................................................................................................................ |
23 |
|
30. |
Волновое уравнение для электромагнитного поля в вакууме. Плоские монохроматические |
|
волны и их свойства. Поляризация электромагнитных волн. .......................................................... |
23 |
|
31.Оптические спектральные приборы (призменные, дифракционные, интерференционные). 23
32.Распространение света в веществе: дисперсия, фазовая и групповая скорости, комплексный
показатель преломления....................................................................................................................... |
24 |
|
33. |
Дифракция электромагнитных волн (приближения Гюйгенса–Френеля и Фраунгофера)... |
25 |
34. |
Распространение света в анизотропных средах. ....................................................................... |
25 |
Атомная физика. Квантовая механика................................................................................. |
27 |
|
35. |
Дифракция электронов, атомов, молекул и нейтронов. ........................................................... |
27 |
36. |
Принципы усиления и генерации оптического излучения. Среды с инверсной |
|
заселенностью. ...................................................................................................................................... |
27 |
|
37. |
Эффект Зеемана и эффект Штарка. ............................................................................................ |
28 |
38. |
Физические величины и операторы. .......................................................................................... |
28 |
39. |
Состояние квантовой системы, чистое и смешанное. Волновая функция и статистический |
|
оператор................................................................................................................................................. |
29 |
|
40. |
Соотношение неопределенностей, мысленные эксперименты и вывод по Гейзенбергу...... |
30 |
41.Развитие системы во времени. Уравнение Шредингера и квантовое уравнение Лиувилля. 30
42.Стационарные состояния свободной частицы и частицы в потенциальной яме. Туннельный
эффект, надбарьерное отражение........................................................................................................ |
31 |
|
43. |
Оператор момента количества движения. Орбитальный, спиновый и полный моменты. |
|
Магнитный момент электрона. Мультиплетность спектров. ........................................................... |
32 |
|
44. |
Частица в центральном поле. Особенности энергетического спектра частицы в |
|
кулоновском поле. Спектры атома водорода и щелочных металлов............................................... |
33 |
|
45. |
Оптические спектры атомов и молекул. .................................................................................... |
33 |
46. |
Квазиклассические условия квантования. ................................................................................. |
33 |
47. |
Тождественные квантовые частицы. Принцип Паули, его точная и приближенная |
|
формулировки. ...................................................................................................................................... |
34 |
|
Ядерная физика. ........................................................................................................................ |
36 |
|
48. |
Энергия связи. Синтез и деление ядер....................................................................................... |
36 |
49. |
Виды ядерных превращений....................................................................................................... |
37 |
50. |
Модели атомных ядер.................................................................................................................. |
38 |
51. |
Основы систематики элементарных частиц и законы сохранения в микромире................... |
39 |
52. |
Взаимодействия элементарных частиц. Фундаментальные взаимодействия. ....................... |
39 |
Физика твердого тела. .............................................................................................................. |
40 |
|
53. |
Типы сил связи в кристаллах: ионные, ковалентные, ван-дер-Ваальсовы, металлические. |
|
Кристаллические структуры................................................................................................................ |
40 |
|
54. |
Теорема Блоха и ее основные следствия. Обратная решетка. Зоны Бриллюэна. .................. |
41 |
55. |
Зонная модель твердого тела. Формирование энергетических зон и их заполнение |
|
электронами. Роль граничных условий. Энергия Ферми. Приближение сильно и слабо |
|
|
связанных электронов. ......................................................................................................................... |
42 |
|
56. |
Электронные свойства полупроводников. Собственная и примесная проводимость. |
|
Акцепторные и донорные полупроводники....................................................................................... |
42 |
|
57. |
Электронный газ в металлах в приближении свободных электронов. Энергия Ферми и |
|
поверхность Ферми............................................................................................................................... |
44 |
|
58. |
Адиабатическое и одноэлектронное приближение................................................................... |
45 |
59. |
Тепловые колебания кристаллических решеток Температура Дебая. .................................... |
46 |
60. |
Квазичастицы в твердом теле (электроны, дырки, фононы, экситоны, поляроны и др.). |
|
Дисперсионные зависимости, эффективная масса электронов и дырок. ........................................ |
47 |
|
Литература.................................................................................................................................. |
48 |
|
GosPhys8 v7.02 Copyright © 2006 Davyd Tsurikov |
e-mail: DavydTsurikov@mail.ru 2 |
Механика.
Сокращения. |
|
|
|
система:=механическая система |
скорости:=обобщённые скорости |
||
координаты:=обобщённые координаты |
ускорения:=обобщённые ускорения |
||
Обозначения. |
|
|
|
q :={qi }N |
– совокупность координат системы |
N – число степеней свободы системы |
|
i=1 |
|
RN {q (t )}t2 |
|
q :={qi }N |
– совокупность скоростей системы |
– траектория системы |
|
i=1 |
|
t=t |
|
|
|
1 |
|
x :={xi }i – совокупность радиус-векторов материальных точек |
|||
xi := (xi1, xi2 , xi3 ) – радиус-вектор i -ой частицы |
|
||
dt – полная производная по времени |
∂t – частная производная по времени |
||
Соглашения.
По повторяющимся значкам – суммирование. Скалярные произведения векторов записываются в форме бра-кет. Местами для сокращения опущены пределы интегрирования и немые символы у подынтегральных функций.
1. Обобщенные координаты. Функция Лагранжа. Принцип наименьшего действия.
Обобщённые координаты – совокупность величин, полностью характеризующих положение механической системы в пространстве. ([1] с. 9)
Число степеней свободы – полное число обобщённых координат.
Утв. Одновременное задание координат и скоростей системы однозначно определяет её состояние. ( опыт)
Замечание. Знание состояния системы в данный момент времени позволяет предсказать её состояние в произвольный момент времени.
Уравнения движения – уравнения, связывающие ускорения с координатами и скоростями системы; позволяют найти q . ([1] с. 10)
Принцип наименьшего действия (принцип Гамильтона). Функция L , отвечающая
t2
минимуму функционала S (q):= ∫dtL (q (t ), q (t ),t ), однозначно характеризует систему.
t1
L : R2 N +1 → R – функция Лагранжа
t2
S (q):= ∫dtL(q (t ), q (t ),t ) – функционал действия
t1
Получение уравнения Лагранжа, исходя из принципа наименьшего действия.
0 =δS (q)= S (q +δq)− S (q)= ∫dtL(q +δq, dt [q +δq],t )− ∫dtL (q, dt q,t )=
= ∫dtL (q +δq, q +δq,t )− ∫dtL(q, dt q,t ) |
|
|
|
|
|
|
|
L (q +δq, q +δq,t )≈ L (q, q,t )+ ∂q L(q, q,t ) δq + ∂q L(q, q,t ) δq |
|
||
|
|
||
|
|
|
|
GosPhys8 v7.02 Copyright © 2006 Davyd Tsurikov |
e-mail: DavydTsurikov@mail.ru 3 |
||
|
|
|
δdt q=dtδq |
|
|
|
|
|
|
|
|
|
0 = ∫dt |
∂q L δq + ∂q L δq |
= |
|
∫dt ∂q L δq + ∂q L dtδq |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dt ∂q L δq = dt ∂q L δq + ∂q L dtδq = dt∂q L δq + ∂q L dtδq |
|
|
||||||||||
|
|
|||||||||||
|
|
∂q L δq + dt ∂q L δq − |
dt ∂q L δq |
|
= |
|
|
|||||
0 = ∫dt |
|
|
|
|||||||||
= dt ∂q L −dt ∂q L δq + ∂q L δq |
t2 |
( 1 ) |
( |
t |
2 ) |
=0 |
|
|
||||
∫ |
|
|
|
|
δq t |
=δq |
|
|
|
|
||
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
▲∂q L −dt ∂q L = 0 уравнение Лагранжа
Замечание. L =T −U – функция Лагранжа для консервативных систем. T – кинетическая энергия, U – потенциальная энергия.
Свойства функции Лагранжа.
1. La+b = La + Lb – функция Лагранжа системы a +b , состоящей из двух независимых подсистем a и b
2.Очевидно, что из принципа наименьшего действия функция Лагранжа определяется с точностью до аддитивной функции dt F (q,t ), т.к. уравнения Лагранжа для функций L1
и L2 (q, q,t ):= L1 (q, q,t )+ dt F (q,t ) совпадают.
2. Законы сохранения импульса, момента импульса и энергии. Их связь с однородностью и изотропностью пространства и однородностью времени.
Интеграл движения – функция координат и скоростей, остающаяся постоянной при движении системы и зависящая только от начальных условий. ([1] с. 24)
Число интегралов движения для системы с N степенями свободы – 2N −1 Аддитивный интеграл движения – интеграл движения, значение которого для системы
равно сумме его значений для невзаимодействующих (?) подсистем, составляющих данную систему.
Однородность времени. L ≠ L (t ) (требование для замкнутой системы)
|
|
dt L(q, q)= ∂q L q + ∂q L dt q = ∂q L q + dt ∂q L q − dt∂q L q |
||||||||||||||
d |
∂ |
|
L −∂ |
|
L q |
= d |
∂ |
|
L q − L |
|
dt ∂q L−∂q L=0 |
|
L q − L = const |
|
|
|
|
|
|
|
∂ |
|
|
|
|||||||||
t |
|
q |
|
q |
|
|
t |
q |
|
|
|
|
q |
|
|
|
p := ∂q L − обобщённыйимульс |
|
E := |
p q − L − энергия |
|
|
|||||||||||
|
|
|
||||||||||||||
▲E = const закон сохранения энергии
Однородность пространства. Механические свойства системы не изменяются при любом параллельном переносе системы как целого в пространстве (ДПСК): δL(x)= 0
0 =δL (x)= L (x +δ x)− L (x)= L (x +δ x)− L (x, x)≈ L (x)+ ∂x L δ x − L (x)
∂x L = 0 |
dt ∂x L−∂x L=0 |
p=∂x L |
|
dt ∂x L = 0 ∂x L = const |
▲p = const закон сохранения импульса
GosPhys8 v7.02 Copyright © 2006 Davyd Tsurikov |
e-mail: DavydTsurikov@mail.ru 4 |
Замечание. Импульс системы равен сумме импульсов частиц её составляющих (вне зависимости от наличия взаимодействия между ними). Проекция импульса сохраняется в том случае, когда потенциальная энергия не зависит от соответствующей декартовой координаты. ([1] с. 27)
Изотропия пространства. Механические свойства системы не изменяются при
|
|
|
|
|
|
|
|
|
|
|
||||||||
повороте системы как целого |
δL(x, x)= 0, |
δ xi |
=δϕ× xi |
|
|
|
|
|
|
|
||||||||
|
|
... |
|
|
|
dt ∂x L−∂x L=0 |
|
|
|
|
|
p:=∂x L |
|
|
||||
0 =δL(x, x)≈ ∂x L δ x + ∂x L δ x |
|
= |
|
dt∂x L δ x + ∂x L δ x |
= |
p δ x |
+ p δ x = |
|||||||||||
|
|
δ x =δϕ×x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= pi δ xi |
+ |
pi δ xi |
i = |
i |
pi δϕ× xi |
+ pi |
δϕ× xi |
= |
|
|
|
|
|
|
|
|||
= δϕ x × p |
+ δϕ x |
× p |
|
|
x × p |
+ x |
× p |
= 0 |
|
d |
x |
× p |
|
= 0 |
|
|
||
i |
i |
i |
i |
|
|
i |
i |
i |
i |
|
|
|
t [ i |
i ] |
|
|
|
|
M := x × p − моментимпульса системы |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
▲M = const закон сохранения момента импульса
Замечание. Момент импульса – аддитивный интеграл движения (вне зависимости от наличия взаимодействия между частицами).
Утв. Любая замкнутая система всегда имеет семь аддитивных интегралов движения:
E , p , M . ([1] с. 32)
3. Движение в центральном поле. Интегралы движения. Уравнение траектории.
Локальные обозначения: r – радиус-вектор, x, y, z – координаты частицы в ДПСК,
модули векторов – курсив, вектора – жирный курсив, Утв. При движении в центральном поле выполняется закон сохранения момента
импульса: |
|
|
|
|
|
|
|
|
M = const |
|
|
|
движение происходит в плоскости, уравнение которой |
M r = 0 |
|||
M = r × p |
|
|
||||||
|
|
|
|
|
|
|
|
|
Введём ПСК в плоскости движения M r = 0 |
|
|
||||||
x = r cosϕ, |
y = r sinϕ x = r cosϕ −rϕ sinϕ, y = r sinϕ + rϕ cosϕ |
|
|
|||||
|
|
|
|
|
|
|
... |
|
L =T −U = |
m |
(x |
2 |
+ y |
2 |
)−U |
|
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
L (r, r,ϕ)= m2 (r2 + r2ϕ2 )−U (r )
В данном случае ϕ – циклическая координата, т.к. функция Лагранжа не зависит от
неё явным образом. |
|
|
|
|
|
|
|
|
|
|||
Утв. qi – циклическая |
|
|
pi |
– интеграл движения |
||||||||
очевидно из уравнения Лагранжа и определения обобщённого импульса▲ |
||||||||||||
Уравнение Лагранжа для ϕ примет вид: |
|
|||||||||||
dt ∂ϕ L = 0 |
▲ |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
pϕ = mr |
ϕ = const |
|
|
|
||||||
M = rp = m |
(x |
|
+ y |
|
)(x |
|
+ y |
|
... |
|
M = const , т.е. M – интеграл движения |
|
|
|
|
|
)=mr ϕ |
|
|
||||||
|
|
2 |
|
2 |
|
2 |
|
2 |
|
2 |
|
|
Т.к. функция Лагранжа явно не зависит от времени, то E – интеграл движения. |
||||||||||||
GosPhys8 v7.02 Copyright © 2006 Davyd Tsurikov |
e-mail: DavydTsurikov@mail.ru 5 |
|||||||||||
Нахождение r и уравнения траектории с помощью интегралов движения E и M ([1]
с. 47)
|
|
m |
r |
2 |
2 2 |
+U |
(r ) |
ϕ=M /(mr2 ) m |
|
2 |
|
|
|
M 2 |
|
+U (r )=: |
mr2 |
|
|
|
|
|
(r) |
|
||||||||||||||||||||||||||
|
E = |
|
|
|
+ r |
ϕ |
|
|
|
|
= |
|
|
|
r |
|
+ |
|
|
|
|
|
|
|
+V |
|
||||||||||||||||||||||||
2 |
|
|
|
|
|
2 |
|
|
|
|
2 |
r |
2 |
2 |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
r2 = |
2 |
E −V |
( |
r |
|
d |
r = ± |
2 |
E −V |
( |
r |
|
|
|
|
|
dr = ± |
|
2 |
E −V |
( |
r |
dt |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
m |
|
|
|
|
) |
|
|
|
|
|
|
t |
|
|
m |
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
m |
|
|
|
|
) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
t (r)= t0 ± |
|
m ∫r |
d ρ |
|
|
|
|
|
1 |
|
|
, |
|
V (r)= |
μ22 |
|
+U (r), |
μ := |
|
|
|
M |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
E −V (ρ) |
|
|
|
2m |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 rmin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
M = mr2ϕ dϕ = |
|
|
M dt |
|
|
|
dϕ = ± M |
|
|
2 E −V (r ) |
−1/ 2 |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
dr |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt=▲ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
mr |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
mr |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
▲ |
ϕ (r )=ϕ0 ± μ ∫ d ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнение траектории |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
ρ |
2 |
|
|
|
E −V (ρ) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
rmin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Замечание. В уравнении траектории знак ± означает, что имеются две ветви траектории, расположенные симметрично относительно прямой, проходящей через начало координат под углом ϕ0 , что имеет место в случае инфинитного движения (и только?).
В зависимости от вида потенциала U возможны два типа движения:
t r (t ) [rmin ,∞) – инфинитное движение t r (t ) [rmin , rmax ] – финитное движение Область значений r является решением неравенства: E −V (r )≥ 0
Точки поворота – корни уравнения E −V (r )= 0 . Очевидно, что точках поворота r = 0 .
Таким образом, движение в центральном поле полностью определяется видом потенциала U и значениями параметров E и M .
4. Рассеяние частиц неподвижным силовым центром. Дифференциальное сечение рассеяния. Формула Резерфорда.
Рассмотрим случай инфинитного движения, т.е. имеется единственная точка поворота rmin . Частица с энергией E налетает на рассеивающий центр из бесконечно удалённой
точки.
Уравнение траектории:
ϕ(r )=ϕ0 ± μ ∫r |
d ρ |
|
|
|
1 |
, E −V (rmin )= 0, |
V (r )= |
μ22 |
+U (r ), μ := |
M |
||||
ρ |
2 |
E −V (ρ) |
2m |
|||||||||||
rmin |
|
|
+∞ |
|
|
|
|
|
r |
|
||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t → −∞ ϕ → 0 |
|
|
▲ |
= μ ∫ d ρ |
|
|
1 |
|
▲ |
|
ϕ(rmin )=ϕ0 |
|
||
|
|
|
|
|
ϕ0 |
|
|
|
|
|
|
|||
2 |
|
|
|
ρ |
2 |
E −V (ρ) |
|
|||||||
t → −∞ r → +∞ |
|
|
rmin |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Пояснения.
1.Выбор СК.
2.Частица налетает из бесконечно удалённой точки
θ:=π −2ϕ0 – угол рассеяния
От параметров E и M перейдём к новым параметрам задачи.
GosPhys8 v7.02 Copyright © 2006 Davyd Tsurikov |
e-mail: DavydTsurikov@mail.ru 6 |
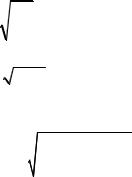
E =: |
mυ∞2 |
|
υ∞ = |
2E |
– скорость частицы на бесконечности |
||||||||||||
|
m |
||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
▲ |
M |
|
– прицельное расстояние |
|
||||||||||
M =: bmυ∞ |
b = |
|
|
|
|||||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
2mE |
|
|
|
|
|
|
|
|
|
|||
Выражение для угла рассеяния примет вид: |
|
|
U (rmin ) |
|
|||||||||||||
|
|
|
+∞ |
|
1 |
|
|
|
|
b2 |
|
||||||
θ (b, E):=π −2b ∫ d ρ |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
, 1− |
|
+ |
|
= 0 |
|||||
|
|
|
b |
2 |
|
U (ρ) |
|
2 |
E |
||||||||
|
|
|
rmin |
ρ2 |
1− |
|
+ |
|
|
rmin |
|
||||||
|
|
|
|
|
ρ2 |
E |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Сопоставление с экспериментом.
поток невзаимодействующий между собой частиц, налетающих на рассеивающий силовой центр. Исходя из симметрии задачи, перейдём в ЦСК.
dσ = 2πbdb = 2πb∂θbdθ |
|
dσ = 2πb∂θb |
dΩ |
|
|||
dΩ = 2π sinθdθ |
|
|
|
||||
|
2π sinθ |
||||||
|
|
|
|
||||
σΩ := dΩσ = |
b |
∂θb |
дифференциальное сечение рассеяния |
||||
sinθ |
|||||||
|
|
|
|
|
|
||
Дифференциальное |
сечение определяет приращение телесного угла рассеяния, |
соответствующего приращению площади кольца. |
|
dN = n2πbdb =: ndσ |
dN = nσΩdΩ – физический смысл дифференциального |
сечения рассеяния.
dN – число налетающих частиц, проходящих через кольцо 2πbdb , а также число рассеянных частицы в соответствующий телесный угол dΩ, в единицу времени
n – плотность потока налетающих частиц
σ := ∫dσ = ∫dΩσΩ = 2ππ∫dθσΩ |
интегральное сечение рассеяния |
0 |
|
Замечания.
1.В эксперименте регистрируется число частиц dN , рассеянных в телесный угол dΩ, что позволяет, зная n , найти σΩ . Зная потенциал U и параметры E и b , можно найти теоретическое значение σΩ . Также можно поставить задачу на изучение неизвестного потенциала U , экспериментально исследуя зависимость σΩ от E и b .
2.σ < ∞ только для финитных потенциалов.
|
Вывод формулы Резерфорда. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
U (r )= − λ |
|
|
|
|
|
|
|
|
|
|
|
|
tan π −θ = 2Eb |
|
b = |
|
λ cot θ |
||||||||||
|
tanϕ0 = |
2Eb |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
...▲ |
|
|
|
|
|
|
|
|
|
|
θ=π −2ϕ0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
λ |
|
|
|
|
λ |
|
|
|
|
|
2E |
|||||||
|
|
|
b |
▲ |
|
|
|
λ2 |
|
|
|
θ |
θ |
|
|
λ2 |
|
|
cos θ2 |
1 |
|
1 |
|
|
|||||
|
σΩ = |
|
|
∂θb |
|
σΩ = |
|
|
|
cot |
|
∂θ cot 2 |
= |
|
|
|
|
2 |
|
|
|
||||||||
|
sinθ |
4E2 sinθ |
2 |
|
4E2 2cos θ2 sin θ2 |
|
sin θ2 |
sin2 θ2 |
|
||||||||||||||||||||
▲ |
|
σΩ = |
|
λ2 |
|
, |
E = |
mυ2 |
|
|
формула Резерфорда |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
(4E)2 sin4 θ2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Замечание. Т.к. в формуле фигурирует λ2 , то сечение будет одинаковым для притягивающего и для отталкивающего центров.
GosPhys8 v7.02 Copyright © 2006 Davyd Tsurikov |
e-mail: DavydTsurikov@mail.ru 7 |