Электричество. Электродинамика.

Используем гауссову систему единиц.

	величины		операторы
название	определение	название	определение

радиус-вектор

x

0

=

x

i =

дифференцирование

∂

0

:=

1

∂

,

∂

i

:=

i

: ct,

: xi

c

t

потенциал

A0 :=ϕ,

Ai := A

Даламбера

:= ∂

α

∂α

i

ток

J 0 := cρ,

J i := j

–

Kαβ :=

gαβ −∂α∂β

i

Fαβ := ∂α Aβ −∂β Aα

...

1

0

0

0

−1

тензор поля

F0i = −F

0i

= Ei ,

метрический тензор

g = 0

0

0

0 0 −1 0

Fij

= Fij

= −εijk Hk

0

0

0

−1

21. Теорема Гаусса и ее применение к вычислению электрических полей простейших распределений плотности заряда.

∫dx div a = ∫∫ dsan		теорема Гаусса
V	S

Словами: интеграл по объёму V от дивергенции вектора a равен потоку вектора a через поверхность S , ограничивающую объём V (нормаль наружу).

Простейшие распределения: заряженный шар, заряженный цилиндр.

Алгоритм. Использовать в качестве вектора напряжённость электрического поля E , воспользоваться уравнениями Максвелла. При необходимости рассмотреть пределы.

+произвести расчёт напряжённостей электрических полей для простейших распределений плотности заряда

22. Теорема Стокса и ее применение к вычислению магнитных полей простейших распределений плотности тока.

	∫∫ds (rot a)n = ∫dxiai		теорема Стокса
	S	L
Словами:		поток ротора вектора a через поверхность, ограниченную контуром		L ,
равен циркуляции вектора a по контуру L .
Простейшие распределения: проводник с током, бесконечно длинный соленоид.				H ,
Алгоритм. Использовать в качестве вектора напряжённость магнитного поля
воспользоваться уравнениями Максвелла. При необходимости рассмотреть пределы.

+произвести расчёт напряжённостей электрических полей для простейших

распределений плотности тока
GosPhys8 v7.02 Copyright © 2006 Davyd Tsurikov	e-mail: [e-mail] 18

23. Проводники и диэлектрики в электростатическом поле.

Токи, возникающие в среде при наличии поля: j =σ E

Идеальный металл σ = ∞ .

В ИМ объёмные заряды отсутствуют, возможны только поверхностные. Воспользовавшись интегральной формулировкой уравнения Максвелла для E , имеем:

Напряжённость поля над поверхностью: En = 4πσ, Eτ = 0

В силу свойств ИМ справедлив также эффект экранирования ИМ электрического поля. При расчёте полей зарядов, находящихся вблизи поверхности металла используется

метод изображений.

Идеальный диэлектрик σ = 0 .

Воздействие поля на ИД характеризуется поляризацией, количественной характеристикой которой является вектор поляризации – дипольный момент единицы

объёма: Pidx := ddi .

P =αE ,

где

α –

поляризуемость

Случай однородного

изотропного диэлектрика:

(всегда α > 0 ).

ρсвяз. (x):= −div P

D := E + 4π P = (1+ 4πα)E =:εE

D – вектор электрической индукции.

Статические уравнения Максвелла для диэлектриков: rot E = 0

div D = 4πρсвоб.

24. Система

уравнений

Максвелла

для

напряженности

электрического и

индукции магнитного полей в вакууме.

div H = 0

rot H −

1

∂t E =

4π

j

c

c

div E = 4πρ

rot E +

1

∂t H = 0

c

Пояснения.

div H = 0 –

магнитный

аналог

закона

Кулона,

div E = 4πρ –

дифференциальная формулировка закона Кулона,

rot H −

1

∂t E =

4π

j – закон Ампера (за

c

c

исключением 1c ∂t E – ток смещения Максвелла), rot E + 1c ∂t H = 0 – закон Фарадея.

Воспользовавшись теоремой Гаусса и теоремой Стокса можно получить интегральную формулировку уравнений Максвелла:

	∫∫ dsHn = 0	∫dxi Hi −		1			∂t ∫∫dsEn =	4π	I
				c				c
	S	L					S
	∫∫ dsEn = 4πQ	∫dxi Ei +			1		∂t ∫∫dsHn = 0
					c
	S	L					S
Q := ∫dxρ (x) – заряд в объёме V ,		I := ∫∫dsjn	– ток через поверхность S .
V		S

Замечание. Интегральная формулировка является более универсальной, т.к. в данном случае отсутствует требование гладкости источников.

+получить интегральную формулировку уравнения Максвелла из дифференциальной

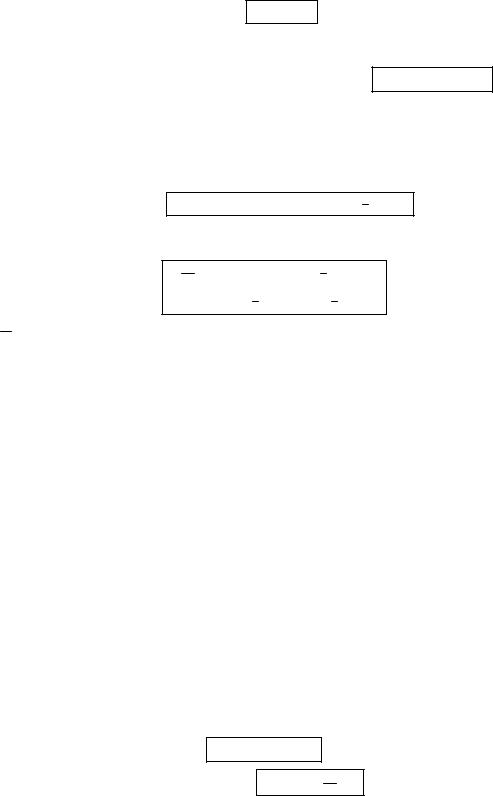
25. Уравнение непрерывности (закон сохранения заряда) в дифференциальной и интегральной формах.

GosPhys8 v7.02 Copyright © 2006 Davyd Tsurikov

e-mail: [e-mail] 19

				∂t
	div E = 4πρ			∂t div E = 4π∂t ρ			div rot=0
									∂t ρ +div j = 0
						cdiv
	rot H −	1	∂t E =		4π	j c div rot H = ∂t div E + 4π div j
		c			c

Т.е. источники в уравнениях Максвелла должны удовлетворять уравнению непрерывности. Воспользовавшись теоремой Гаусса, можно получить интегральную

формулировку уравнения непрерывности: ∂tQ = −I закон сохранения заряда

Словами: заряд не появляется и не исчезает, его изменение в объёме связано с его перетеканием.

Ковариантная формулировка уравнения непрерывности: ∂α Jα = 0 = ∂α Jα

26. Выражения для напряженности электрического и индукции магнитного полей через скалярный и векторный потенциалы. Калибровочная инвариантность.

Определения потенциалов: H =: × A E =: − ϕ − 1c ∂t A

Подставив выражения для потенциалов в уравнения Максвелла, получим уравнения Максвелла для потенциалов:

4cπ j = A + (div A + 1c ∂tϕ)

4πρ = ϕ − 1c ∂t (div A + 1c ∂tϕ)

:= c12 ∂t2 − – оператор Даламбера.

Замечание. Определения потенциалов позволяют однозначно найти напряжённости по известным потенциалам, обратное неверно.

	Калибровочные преобразования –		преобразования	потенциалов, не меняющие
	напряжённостей. Общий вид калибровочных преобразований:
		′	= A + Φ ϕ →ϕ	′			1
	Φ:				=	ϕ + c		∂t Φ
		A → A

Калибровочная инвариантность – калибровочные преобразования потенциалов также являются решениями уравнений для потенциалов. Физическое значение имеют только напряжённости, потенциалы – вспомогательный математический аппарат.

Калибровочные условия (калибровка) – условия, которые накладываются на потенциал с целью устранения калибровочного произвола.

Допустимая калибровка – калибровка, которой всегда можно удовлетворить выбором калибровочного преобразования, т.е. выбором соответствующей функции Φ (технически достаточно доказать существование функции Φ ).

калибровка	условие			уравнения Максвелла
кулоновская	div A = 0			ϕ = 4πρ			A +	1	∂tϕ =	4π	j
								c		c
лоренцева	div A +	1	∂tϕ = 0	A =	4π	j	ϕ = 4πρ
		c			c

Ковариантные формулировки.

Калибровочные преобразования: A′α = Aα +∂α Φ

Уравнения Максвелла для потенциалов: Kαβ Aβ = 4cπ Jα

Лоренцева калибровка: ∂α Aα = 0

GosPhys8 v7.02 Copyright © 2006 Davyd Tsurikov

e-mail: [e-mail] 20