Госы 5к Надя / лекции_3 / int_ zaw_ot_ par / Математический анализ - Интегралы - Аксёнов - 2000 - 145

≤ x ≤

π

;

π

π

≤ x ≤ π;

0 ≤ y ≤

3π

(D ) = 0

2

2

− x ≤ y ≤ π

и (D ) =

2

2

− x .

2

3

Имеем поэтому

I = ∫∫cos( x + y) dxdy = ∫∫cos( x + y) dxdy − ∫∫cos(x + y) dxdy −

( D )

( D1 )

( D2 )

− ∫∫cos( x + y) dxdy + ∫∫cos(x + y) dxdy =

( D3 )

( D4 )

π 2

y=π 2−x

π 2

y=π

= ∫

dx

∫cos(x + y) dy − ∫

dx

∫cos( x + y) dy −

0

y=0

0

y=π 2−x

π

y=3π 2−x

π

y=π

− ∫ dx

∫cos(x + y) dy + ∫

dx

∫cos(x + y) dy =

π 2

y=0

π 2

y=3π 2−x

π 2

y=π

−x

π 2

y=π

π

y=3π

−x

= ∫ sin (x + y)

2

dx − ∫sin ( x + y)

y=π−x dx − ∫sin (x + y)

2

dx +

y=0

y=0

0

0

2

π 2

π

y=π

π 2

π 2

+ ∫ sin (x + y)

−x dx =

∫(1−sin x) dx + ∫(1+sin x) dx +

y=3π

π 2

2

0

0

π

π

π 2

π

+ ∫(1+sin x) dx + ∫(1−sin x) dx = 2 ∫dx + 2 ∫dx = π + π = 2π.

π 2

π 2

0

π 2

Задача 5. Вычислить I = ∫∫sgn (x2 − y2 +2)dxdy, где (

) ={x2 + y2 ≤ 4}.

D

( D )

x

2

− y

2

+ 2 = 0

y

2

−

x2

=1. Вет-

y

( 2)2

(

2)2

ви этой гиперболы являются линиями разрыва подынтегральной функции. Так как подынтегральная функция – ограниченная в (D ) и непрерывная там всюду, за исключением точек, лежащих на двух простых кривых, то двойной интеграл I существует.

Пусть

(D1 ) = {−1 ≤ x ≤1; x2 + 2 ≤ y ≤ 4 − x2 }, (D3 ) = {−1 ≤ x ≤1; − 4 − x2 ≤ y ≤ − x2 + 2},

2

x

−2 −1

1 2

− 2

Рис. 2.17. К задаче 5

51

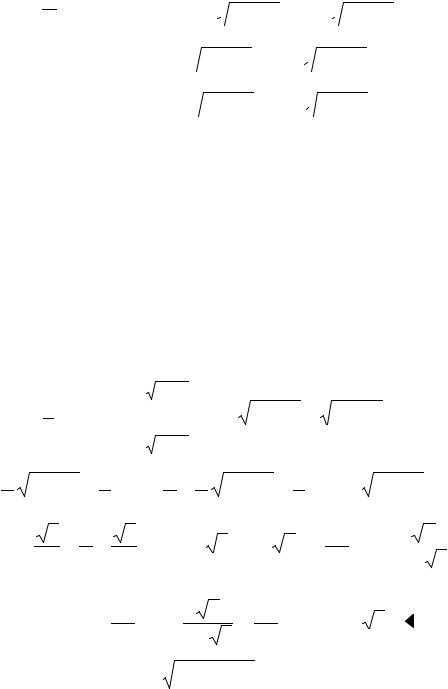
(D2 ) = {−2 ≤ x ≤ −1; − 4 − x2 ≤ y ≤ 4 − x2 }U U{−1 ≤ x ≤1; − x2 + 2 ≤ y ≤ x2 + 2}U U{1 ≤ x ≤ 2; − 4 − x2 ≤ y ≤ 4 − x2 }.

Имеем в (D1) U(D3 ) : x2 − y2 + 2 < 0 , а в (D2 ) : x2 − y2 + 2 > 0 . Мы знаем, что существование и величина двойного интеграла не зависят от значений, принимаемых подынтегральной функцией вдоль конечного числа простых кривых. Поэтому

I = ∫∫dxdy − ∫∫dxdy − ∫∫dxdy = F

− F

− F

,

D2

D1

D3

где F

, F

, F

( D2 )

( D1 )

( D3 )

F(

– площади областей (

(

(

) = 4π,

D1 ) ,

D2 ) ,

D3 ) . Так как

D

D

D

D

1

2

3

F(

) = F(

) , то F(

) = 4π −2F(

) и, следовательно,

I = 4π −4F(

) . Так как

D

D

D

D

D

3

1

2

1

1

область (

D1 ) симметрична относительно оси Oy , то

1

y= 4−x2

1

( 4 − x2 − x2 + 2)dx =

F( D1 ) = 2∫dx ∫dy = 2∫

0

y= x2 +2

0

ln (x +

x

4

− x

2

+

4

arcsin

x

−

x

x

2

+ 2

−

2

x

2

x=1

= 2

2

2

2

2

+ 2)

=

2

x=0

=

2

3 + π −

3 − ln

1+

3

)

+ ln

2

= 2π

+ 2ln

2

.

2

3

2

(

3

1 +

3

	А тогда	8π			2		4π	+ 4ln (2 + 3).
	I = 4π −		−8ln			=
		3			1+ 3		3
	Задача 6. Вычислить I = ∫∫			E( y − x2 ) dxdy , где (						) = {x2 ≤ y ≤ 4}.
									D
			( D )

По определению функции E , имеем:

если 0 ≤ y − x2 <1, т. е. если x2 ≤ y <1+ x2 , то E( y − x2 ) = 0 ; если 1 ≤ y − x2 < 2 , т. е. если 1 + x2 ≤ y < 2 + x2 , то E( y − x2 ) =1; если 2 ≤ y − x2 < 3 , т. е. если 2 + x2 ≤ y < 3 + x2 , то E( y − x2 ) = 2 ; если 3 ≤ y − x2 < 4 , т. е. если 3 + x2 ≤ y < 4 + x2 , то E( y − x2 ) = 3.

52

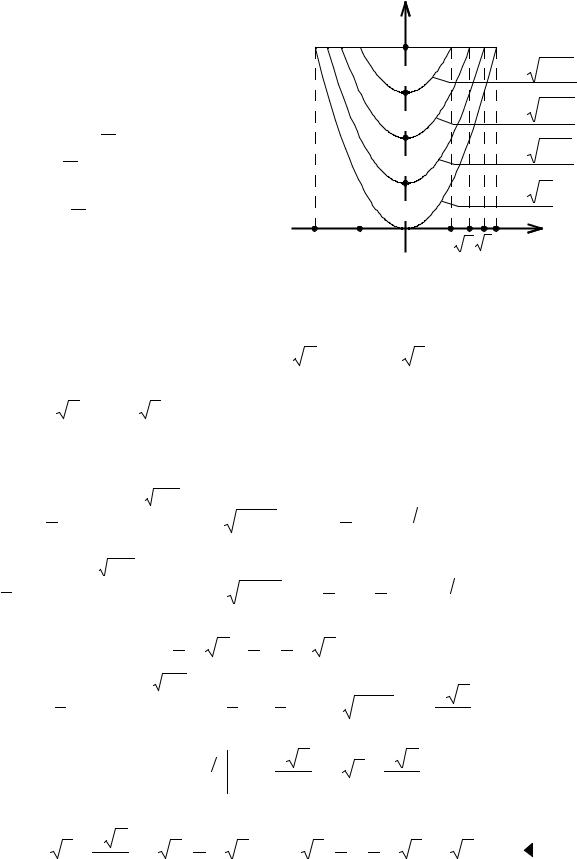
	Следовательно,	E( y − x2 ) = 0	в	(D ) ;		y
				1
	E( y − x2 ) =1 в (D ) ; E( y − x2 ) = 2 в
		2				4
	(D3 ) ; E( y − x2 ) = 3 в (D4 ) . Видим, что						x=	y−3
						(D4)
	подынтегральная функция терпит разрыв					3	x=	y−2
	на конечном числе простых кривых, ле-					(D3)
	жащих в области (D ). В остальных точ-					2	x=	y−1
	ках области (D ) она непрерывная. Так					(D2)	x=	y
	как подынтегральная функция еще и ог-					1
	раниченная в (D ), то двойной интеграл				−2	(D1)		x
	I существует.	Принимая во	внимание,			−	1 2 32
						1
	что существование и величина двойного					Рис. 2.18. К задаче 6
	интеграла не зависят от значений,			при-

нимаемых подынтегральной функцией вдоль конечного числа простых кривых, можем написать, что:

						I = ∫∫0 dxdy + ∫∫1 dxdy + ∫∫																					2 dxdy + ∫∫															3 dxdy
							( D1 )						( D2 )							( D3 )																	( D4 )
I = F						+	2 F				+	3 F			, где F								, F							, F						– площади областей (
																																																							D2 ) ,
				D					D					D						D							D						D
2								3					4							2						3									4
(
	D3 ) , (D4 ) соответственно. Так как области (D2 ) , (D3 ) , (D4 ) симметричны
относительно оси Oy , то:
						FD4		4			x=		y−3			4		y −3 dy =												2		2			( y −							3 2			y=4					4	;
							= 2∫dy ∫dx = 2∫																									3								3)					=					3
								3				x=0				3																													y=3
						4		x= y−2									4		y − 2 dy −											4		=				2	2			( y −				3 2					y=4				4	=
		FD3 = 2∫dy ∫dx − FD4 = 2∫																												3							3							2)							−		3
						2		x=0					3				2		3					3 (											)														y=2
													= 4 2 2					− 4		=				4		2 2 −									1 ;
								4			x=		y−1																	4
						FD2		= 2∫dy ∫dx −( FD3											+ FD4 ) = 2∫ y −1 dy − 8 32 =
								1				x=0				3 2 y=4														1
												2										8			2													8				2
								=			2	3	( y −1)					y=1 −						3					= 4 3 −											3			.
А тогда
		I =				4 3 − 8 2						+	2		4	(	2 2 −1							+ 3 4											= 4			(		4 3 −3 2 +											4	)	.
								3							3							)								3					3

53

Глава 3. Криволинейные интегралы

§1. Криволинейные интегралы первого рода

1°. Прежде чем дать определение криволинейного интеграла первого рода, рассмотрим следующую задачу.

Имеется спрямляемая пространственная кривая (l) длины s . Пусть на (l) непрерывным образом распределена масса с плотностью ρ( x, y, z) . (Средней

плотностью дуги мы называем отношение ее массы к ее длине. Плотность ρ( x, y, z) кривой (l) в точке ( x, y, z) есть предел средней плотности бесконеч-

но малой дуги, стягивающейся в упомянутую точку). Требуется найти массу m

кривой (l).			Разбиваем кривую				(l)	точками
z		B=An
		An−1	A0 = A,		A1, A2 , K ,		An−1,	An = B
			произвольным образом на n частичных
		Ak+1	дуг Ak Ak+1 ( k = 0, 1, 2, K, n −1) с дли-
A=A0			нами s0 , s1, s2 , K, sn−1 . Полагаем
		A
		k	λ = max {s }. Предполагаем частич-
A	A2	y	k=			k
				0, n	−1
1			ные дуги Ak Ak+1 столь малыми, что на
x			(Ak Ak+1			плотность	распределения
			массы ρ вдоль этой дуги можно при-
Рис. 3.1. К задаче по определению массы			ближенно считать постоянной, равной
кривой			ρ( xk , yk , zk ), где точка ( xk , yk , zk ) –
любая, принадлежащая		(Ak Ak+1 . Тогда масса			∆mk частичной дуги			Ak Ak+1

привой (l) будет приближенно выражаться формулой

∆mk = ρ( xk , yk , zk ) sk .

Масса m всей кривой (l) будет выражаться приближенно суммой

m ≈ ρ( x0 , y0 , z0 ) s0 +ρ( x1, y1, z1) s1 +K+ρ( xn−1, yn−1, zn−1) sn−1 =

n−1

= ∑ρ( xk , yk , zk ) sk .

k=0

Интуитивно ясно, что чем мельче частичные дуги Ak Ak+1, тем меньше ошибка, которую мы делаем, считая частичную дугу Ak Ak+1 однородной. Поэтому за массу m кривой (l) естественно принять:

n−1

m = lim ∑ρ( xk , yk , zk ) sk .

λ→0 k=0

54

2°. Дадим теперь определение криволинейного интеграла первого рода. Пусть в пространстве расположена спрямляемая кривая (l), имеющая концы в точках A и B, и пусть во всех точках кривой (l) определена функция

f( x, y, z) . Проделаем следующие операции.

1.Разобьем кривую (l) точками A0 = A, A1, A2 , K , An−1, An = B , следующими друг за другом вдоль кривой (l) в направлении от A к B, на частич-

ные дуги (Ak Ak+1 . Пусть sk – длина (Ak Ak+1 ( k = 0, 1, K, n −1). Положим
λ = max {s			} ( λ – ранг дробления).
k=		k
	0, n−1

2.На каждой дуге (Ak Ak+1 берем произвольную точку ( xk , yk , zk ) и вычисляем в ней значение функции f , т. е. находим f ( xk , yk , zk ) .

3.Умножаем найденное значение функции на длину соответствующей частичной дуги: f ( xk , yk , zk ) sk , k = 0, 1, K, n −1.

4.Складываем все такие произведения. Получаем сумму

n−1

σ = ∑ f ( xk , yk , zk ) sk .

k=0

Отметим, что значение суммы σ зависит, вообще говоря, как от способа раз-

биения кривой (l) на части (Ak Ak+1 , k = 0, n −1, так и от выбора точки

( xk , yk , zk ) на (Ak Ak+1 .

5. Измельчаем дробление так, чтобы λ → 0 , и ищем lim σ. Если существу-

λ→0

ет конечный предел I = lim σ и этот предел не зависит ни от способа разбие-
	λ→0
ния кривой	(l) на части	(Ak Ak+1 , k =		, ни от способа выбора точек
			0, n −1
( xk , yk , zk )	на (Ak Ak+1 ,	то его называют криволинейным интегралом первого
рода от функции f ( x, y, z) по кривой (l) и обозначают символом
		∫ f ( x, y, z) ds.			(1)
		(AB
Если, в частности, кривая (l) лежит в плоскости Oxy , то функция f					от ко-
ординаты z не зависит, и вместо (1) появляется интеграл
		∫ f ( x, y) ds .			(2)

(AB

Замечание 1. Из самого определения криволинейного интеграла первого рода вытекает следующее свойство:

∫ f ( x, y, z) ds = ∫ f ( x, y, z) ds ,

(AB

(BA

55

т. е. направление, которое может быть придано пути интегрирования, никакой роли не играет. В самом деле, ведь длина sk дуги (Ak Ak+1 не зависит от того,

какая из точек Ak и Ak+1 принята за начало и какая – за конец дуги. Замечание 2. Принимая во внимание определение криволинейного интегра-

ла первого рода, можно заключить, что в задаче пункта 1° масса m кривой (l)

определяется по формуле: m = ∫ρ( x, y, z) ds .

(AB

3°. Теорема (о существовании и вычислении криволинейного интеграла

первого рода по плоской кривой).

x = ϕ(t),	t [ p,q], где ϕ и ψ
1. Пусть кривая (AB задана уравнениями:
y = ψ(t),

– функции, заданные на промежутке [ p,q] и имеющие там непрерывные производные ϕ′(t) , ψ′(t) . Пусть (ϕ( p), ψ( p))= A , (ϕ(q), ψ(q))= B . Пусть точки

(ϕ(t), ψ(t)) следуют друг за другом на (AB именно в том порядке, в каком соответствующие значения t следуют друг за другом на [ p,q]. (Считаем (AB

незамкнутой и не имеющей кратных точек.)

2. Пусть функция f ( x, y) задана на (AB и непрерывна там.

Тогда I = ∫ f ( x, y) ds существует и выражается обыкновенным определен-

(AB

ным интегралом по формуле:

	q
∫ f ( x, y) ds = ∫ f (ϕ(t), ψ(t)) (ϕ′(t))2 +(ψ′(t))2 dt ( p < q) .		(3)
(AB	p

(подчеркнем, что нижний предел определенного интеграла (3) должен быть меньше верхнего).

Заметим сначала, что интеграл, стоящий в правой части (3), существует, ибо подынтегральная функция в нем непрерывна на промежутке [ p,q].

Напомним, что в условиях теоремы кривая (AB спрямляема и ее длина s

	q
равна: s = ∫ (ϕ′(t))2 +(ψ′(t))2 dt					( p < q). Составим сумму Римана σ для кри-
	p
волинейного интеграла			∫ f ( x, y) ds . Для этого надо разбить (AB точками Ak
	Ak Ak+1 ( k =		(AB
на дуги				). Такое разбиение можно осуществить,			если раз-
		0, n −1
бить	промежуток		[ p,q]		произвольным	образом	точками

t0 = p < t1 < t2 <K< tn = q и положить Ak = (ϕ(tk ), ψ(tk )), k = 0, n . Тогда

56

tk+1	(ϕ′(t))2 +(ψ′(t))2 dt, k = 0, n −1.
sk = ∫					(4)
tk
Затем на каждой частичной дуге (Ak Ak+1			нужно взять произвольную точку
Mk ( xk , yk ) . Это можно	сделать так:	на	каждом	частичном	промежутке
[tk ,tk+1] взять произвольную точку θk		и положить		xk = ϕ(θk ) ,	yk = ψ(θk ) .

Будем иметь тогда:

n−1	n−1	tk+1
σ = ∑ f ( xk , yk ) sk = ∑ f (ϕ(θk ), ψ(θk ))		∫	(ϕ′(t))2 +(ψ′(t))2 dt .
k=0	k=0	tk

По теореме о среднем для определенного интеграла (4)

sk = tk∫+1 (ϕ′(t))2 +(ψ′(t))2 dt = (ϕ′(τk ))2 +(ψ′(τk ))2 (tk+1 − tk ) ,

tk

где τk [tk ,tk+1]. Поэтому

n−1

σ = ∑ f (ϕ(θk ), ψ(θk )) (ϕ′(τk ))2 +(ψ′(τk ))2 ∆tk .

k=0

Полученное выражение для σ сходно с суммой Римана для определенного интеграла, стоящего в правой части (3), но таковой не является, так как θk и τk ,

вообще говоря, различны. Составим сумму

n−1

σ* = ∑ f (ϕ(τk ), ψ(τk )) (ϕ′(τk ))2 +(ψ′(τk ))2 ∆tk .

k=0

Это уже настоящая сумма Римана для определенного интеграла, стоящего в правой части (3), т. е. для интеграла

			q
			I* = ∫ f (ϕ(t), ψ(t))	(ϕ′(t))2 +(ψ′(t))2 dt .
			p
Было	отмечено, что I* существует.			Следовательно, σ* → I*	при λ* → 0
( λ* =	max {∆tk }). Заметим, что (λ → 0) (λ* → 0) . Рассмотрим очевид-
	k=	0, n−1
ное равенство
			σ = σ* +(σ −σ* ).		(5)

Из (5) видно, что теорема будет доказана, если показать, что lim (σ −σ* ) = 0 .

λ*→0

57

Имеем

n−1

σ −σ* = ∑[f (ϕ(θk ), ψ(θk ))− f (ϕ(τk ), ψ(τk ))] sk .

k=0

Возьмем ε > 0 – любое, сколь угодно малое. Функция f (ϕ(t), ψ(t)) C([ p,q]),

как суперпозиция непрерывных функций. Значит, она и равномерно непрерывна на промежутке [ p,q] взятому ε > 0 отвечает δ > 0 такое, что для любых двух точек t′ и t′′ из [ p,q], для которых t′′ −t′ < δ, будет

f (ϕ(t′′), ψ(t′′))− f (ϕ(t′), ψ(t′)) < ε.

Возьмем любое разбиение промежутка [ p,q] на части [tk ,tk+1], у которого ранг

дробления λ* < δ. Так как θk и τk [tk ,tk+1], то θk − τk ≤ tk+1 −tk ≤ λ* < δ. Следовательно, для любого k = 0, n −1 будем иметь:

f (ϕ(θk ), ψ(θk ))− f (ϕ(τk ), ψ(τk )) < ε.

Поэтому, считая				дробление промежутка [ p,q] таким, что λ* < δ, получим
			n−1
	σ −σ*		< ∑ε sk	= ε s (здесь s – длина (AB ). Так как для достижения нера-

k=0

венства σ −σ* < ε s потребовалось лишь, чтобы было λ* < δ, то заключаем,

что lim (σ −σ* ) = 0 , а значит, и lim (σ −σ* ) = 0 .
λ*→0	λ→0
Частные случаи.

I. Пусть кривая (AB дана явным уравнением: y = ϕ(x), x [a,b], a < b . Тогда:

1)	если функция ϕ(x) имеет на промежутке [a,b] непрерывную производ-
ную ϕ′(x) и
2)	если функция	f (x, y) непрерывна на (AB, то ∫ f (x, y)ds существует, и
			(AB
			b
	∫ f ( x, y) ds = ∫ f (x,ϕ( x)) 1 +(ϕ′( x))2 dx .
	(AB		a
II. Пусть (AB		задана	уравнением в полярных координатах: r = r(ϕ) ,

ϕ[α,β], α <β. Тогда:

1)если функция r(ϕ) имеет на промежутке [α,β] непрерывную производную r′(ϕ) и

2) если функция f (x, y) непрерывна на (AB, то ∫ f (x, y)ds существует, и

(AB

58

β

∫ f ( x, y) ds = ∫ f (r cosϕ,r sin ϕ) r2 +(rϕ′)2 dϕ.

(AB

α

Замечание. Совершенно аналогично доказывается теорема о существовании и вычислении криволинейного интеграла первого рода по пространственной кривой.

Теорема.

1.	Пусть пространственная кривая (AB задана уравнениями:
	x = ϕ(t),
		t [ p,q] и p < q
	y = ψ(t),
	z = ω(t),
(считаем (AB незамкнутой и не имеющей кратных точек).
2.	Пусть функции ϕ(t), ψ(t), ω(t)		имеют на промежутке [ p, q] непрерыв-
ные производные ϕ′(t), ψ′(t), ω′(t) .
3.	Пусть (ϕ( p), ψ( p),ω( p))= A,		(ϕ(q), ψ(q),ω(q))= B и точки

(ϕ(t), ψ(t),ω(t)) следуют друг за другом на (AB именно в том порядке, в ка-

ком соответствующие значения t следуют друг за другом на	[ p, q].
Тогда, если функция f ( x, y, z) непрерывна на (AB , то	I = ∫ f ( x, y, z) ds
	(AB

существует и выражается через обыкновенный определенный интеграл по формуле:

q

(ϕ(t), ψ(t),ω(t)) (ϕ′(t))2 +(ψ′(t))2 +(ω′(t))2 dt ( p < q) .

∫ f ( x, y, z) ds =∫ f

(AB

p

Примеры.

y

1. Вычислить I = ∫( x4 3 + y4 3 ) ds , где (l) – дуга

a

(l )

астроиды x2 3 + y2 3 = a2 3.

x

Вычисление I

удобнее производить, взяв урав-

−a

a

нение астроиды (l) в параметрической форме:

3

x

= a cos

t,

t

[0, 2π].

−a

(l) =

3

= a sin

t,

Рис. 3.2. К примеру 1

y

Имеем x′ = −3a cos2 t sin t ;

y

′ = 3a sin2 t cos t ;

t

t

ds =

( x′)2 +( y′)2 =

9a2 sin2 t cos2 t dt = 3a sin t cos t dt .

t

t

Поэтому

59

2π

I = ∫a43(cos4 t +sin4 t) 3a sin t cos t dt =

0
π 2	π
= 3a7 3 ∫(cos5 sin t +sin5 cos t) dt −	∫(cos5 sin t +sin5 cos t) dt +
	π 2
0

3π 2

2π

+ ∫(cos5 sin t +sin5 cos t) dt −

∫(cos5 sin t +sin5 cos t ) dt

π

3π 2

I =

1

a

7 3

6

t +sin

6

t)

π

2

+(cos

6

t −sin

6

t)

π

+

2

(−cos

0

= a7 3

π

2

+(−cos6 t +sin6 t)

3π 2 +(cos6 t −sin6 t) 2π

[

2 + 2

+ 2

+ 2

= 4a7 3.

π

3π

2

]

y

2

ϕ =

3π

ϕ=

π

2. Вычислить

I =

∫ y ds ,

где

(l) – дуга

4

4

x

(l )

−a

a

лемнискаты ( x2 + y2 )2 = a2 ( x2 − y2 ).

ϕ = −

3π

π

Перейдем

к

полярным

координатам:

ϕ=−

x = r cosϕ,

4

4

Тогда уравнение лемнискаты по-

Рис. 3.3. К примеру 2

y = r sin ϕ.

лучим в

виде:

r = a

cos 2ϕ .

Имеем

r′ = −a

sin 2ϕ

;

r2 +(r′)2

=

a2

;

ds =

r2 +(r′)2 dϕ =

a dϕ

;

ϕ

cos 2ϕ

ϕ

cos 2ϕ

ϕ

cos 2ϕ

y = a

cos 2ϕ sin ϕ ,

y

ds = a2

sin ϕ

dϕ. Поэтому

π 4

π

−3π 4

0

I = a2 ∫sin ϕdϕ + ∫sin ϕdϕ −

∫sin ϕdϕ − ∫sin ϕdϕ =

3π 4

−π

−π 4

0

= a2[−cosϕ

0π 4 − cosϕ

3ππ 4 + cosϕ

−π−3π 4 + cosϕ

0−π 4 ]= a2 (4 − 2

2).

3. Вычислить I = ∫( x + y) ds, где (l) – контур треугольника с вершинами в

(l )

точках O(0, 0) , A(1, 0), B(0,1) .

60