1.8.3. Уравнение движения центра масс

Понятие центра масс позволяет придать уравнению, выражающему второй закон Ньютона для системы тел, иную форму. Для этого достаточно представить импульс системы как произведение массы системы на скорость ее центра масс:

Тогда

Получили уравнение движения центра масс, согласно которому центр масс любой системы тел движется так, как если бы вся масса системы была сосредоточена в нем, и к нему были бы приложены все внешние силы. Если сумма внешних сил равна нулю, то , а, значит,, т. е. центр масс (инерции) замкнутой системы покоится или перемещается равномерно и прямолинейно. Другими словами,внутренние силы взаимодействия тел не могут придать какое-либо ускорение центру масс системы тел и изменить скорость его движения.

Скорость центра масс определяется полным импульсом механической системы, поэтому перемещение центра масс характеризует движение этой системы как единого целого.

4. Движение тела переменной массы

Движение некоторых тел происходит благодаря изменению их массы. Рассмотрим движение тела переменной массы на примере ракеты, движущейся благодаря выбросу потока газов, образовавшихся при сгорании топлива. Пусть в некоторый момент отсчета времени t скорость ракеты относительно Земли равна . Выберем для этого момента времени такую систему отсчета, которая движется относительно Земли равномерно и прямолинейно со скоростью равной. В этой системе отсчета ракета в момент времениt покоится. Переменная масса ракеты в этот момент времени равна m. Скорость потока газов относительно ракеты примем постоянной и равной (рис. 1.19). Пусть на ракету действует постоянная сила, например, сила сопротивления атмосферного воздуха.

Рис.1.19.

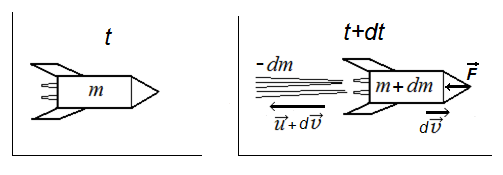
Запишем изменение импульса системы для бесконечно малого промежутка времениdt. В момент отсчета времени t+dt масса ракеты равна m+dm. Так как dm < 0, то отделяемая масса равна – dm. Скорость ракеты за время dt получит приращение . Изменение импульса ракетыравно

Изменение импульса отделяемой массы:

Здесь– скорость отделяемой массы в выбранной нами системе отсчета. Согласно закону изменения импульса неизолированной системы тел

,

откуда следует, что

и

.

Разделив на dt, приходим к уравнению динамики переменной массы, впервые полученному российским физиком Мещерским:

,

или

Величину называютреактивной силой. Эта сила тем больше, чем быстрее изменяется масса тела со временем. Для тела постоянной массы реактивная сила равна нулю. Если масса тела уменьшается, то реактивная сила направлена в сторону, противоположную скорости отделяемой массы Если масса тела увеличивается, то реактивная сила сонаправлена скорости отделяемой массы

Теперь рассмотрим случай, когда внешних сил нет. В проекции направление движения ракеты уравнение Мещерского примет вид:

или

Интегрируя это выражение, получим:

Константу интегрирования C определим из начальных условий. Если в начальный момент отсчета времени t = 0 скорость ракеты равна нулю, а масса, то и Тогда

.

Это соотношение носит имя российского ученого К.Э. Циолковского и лежит в основе ракетостроения.

4. Преобразования Галилея. Классический закон сложения cкоростей. Механический принцип относительности Галилея

Рассмотрим движение материальной точки М в двух инерциальных систе­мах отсчёта ( и ). Пусть системадвижется по отношению к системес постоянной скоростьюв направлении осиOx (рис. 1.20). При­мером будет движение мате­матического маятника в каюте равномерно плыву­щего корабля по отноше­нию к этой каюте (система ₎ и по отношению к бе­регу реки (система ).

Усло­вимся, что в момент времени t = 0 начала координат систем отсчёта исовпадали. Через времяt положение точки в системебудет определяться радиус-вектором. Положение точкиМ в системе определяется радиус-вектором, а в системе- радиус-вектором(см. рис. 1.20). Если принять, что время в обеих системах отсчета течет одинаково, то:

Рис. 1.20.

Эти соотношения получили название преобразований Галилея. В координатной форме:

Чтобы перейти от системы к системе, применим обратные преобразования:

или .

Дифференцируя радиус-вектор по времени, получим классический закон преобразования скорости точки при переходе от одной инерциальной системы отсчёта к другой – закон сложения скоростей:

или ,

где – скорость точкиМ в системе отсчёта (абсолютная скорость),– скорость точкиМ в системе (относительная скорость),

–скорость перемещения системы по отношению к системе(переносная скорость).

Дифференцируя скорость по времени, с учётом того, что, получим

,

т. е. ускорение точки одинаково во всех инерциальных системах отсчёта, или, как говорят, ускорение инвариантно относительно преобразований Галилея.

Согласно Ньютону масса тела – величина постоянная, не изменяющаяся при его движении, т. е. масса является инвариантной величиной во всех инерциальных системах отсчёта, а, следовательно, и сила, действующая на тело (), также инвариантна относительно преобразований Галилея.

Для инерциальных систем отсчёта справедлив принцип относительности Галилея, согласно которому все инерциальные системы по своим механическим свойствам эквивалентны друг другу. Это означает, что никакими механическими опытами, проводимыми «внутри» данной инерциальной системы, нельзя установить, покоится эта система отсчёта или движется. Во всех инерциальных системах отсчёта свойства пространства и времени одинаковы, одинаковы и все законы механики.