Метод Рунге-Кутта третьего порядка рк3

Порядок погрешности метода - Формулы метода:

(6)

Метод Рунге-Кутта четвертого порядка РК4

Наиболее распространен и имеет порядок погрешности h⁵.Формулы метода:

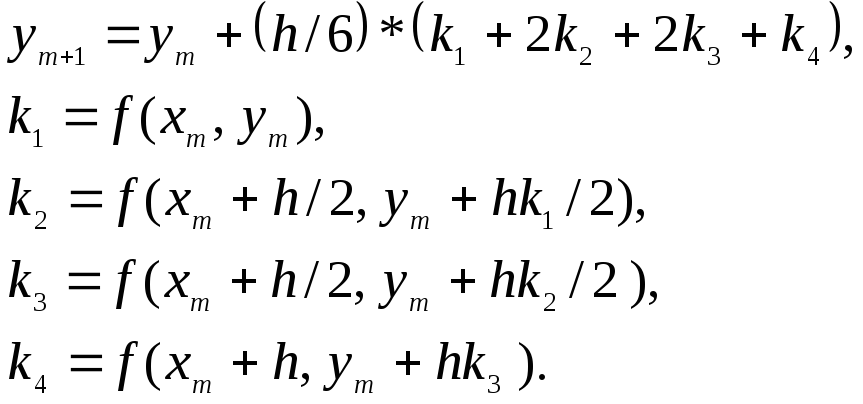(7)

Все вышеприведенные методы называются одношаговымитак как для вычисления достаточно знать лишь- значение решения на предыдущем шагеЭто позволяет использовать их при переменном шаге интегрирования

Ошибки методов

При выборе шага интегрирования исходят из тогочто численные методы интегрирования ОДУ имеют два источника ошибок: метод и вычисленияОшибка метода тем меньшечем меньше шаг интегрирования и оценивается величиной, где-- интервал интегрирования;c- константа;h ^p - погрешность метода

Ошибка вычисленийкоторую называют ещё ошибкой округленияне зависит от шага интегрированияЕсли на одном шаге она равнато накопившаяся от округлений ошибка удовлетворяет неравенству,гдеM- количество шагов интегрирования

Если компьютер работает с округлениемто более вероятна левая границаа при отбрасывании разрядов - праваяПриближенно суммарная ошибка интегрирования может быть определена по формуле

(8)

Из формулы (8) следуетчто по мере уменьшенияhошибка метода убывает и численное решение сходится к точномуНо когда шаг интегрирования слишком малто при больших отрезках интегрирования численное решение начинает расходиться вследствие накопления ошибок округленийКроме тогодля всех методов интегрирования затраты машинного времени обратно пропорциональны шагу интегрирования

Интегрирование систем оду и оду высших порядков

Прикладные задачи часто приводят к системам ОДУ и к ОДУ -го порядкаВ нормальной форме система ОДУ-го порядка имеет вид

(9)

где - неизвестные функции от переменного, а- заданные функции отпеременных

Задача Коши для системы (9) состоит в отыскании решенияудовлетворяющего начальным условиям.

ОДУ -го порядка разрешают относительно старшей производной

(10)

и введением новых переменных по правилу приводят к нормальной системе ОДУ первого порядка

(11)

с начальными условиями

(12)

Решением ОДУ(10) является n раз дифференцируемая функция которая обращает уравнение (10) в тождество и удовлетворяет начальным условиям (12)

Напримердля решения системы ОДУ

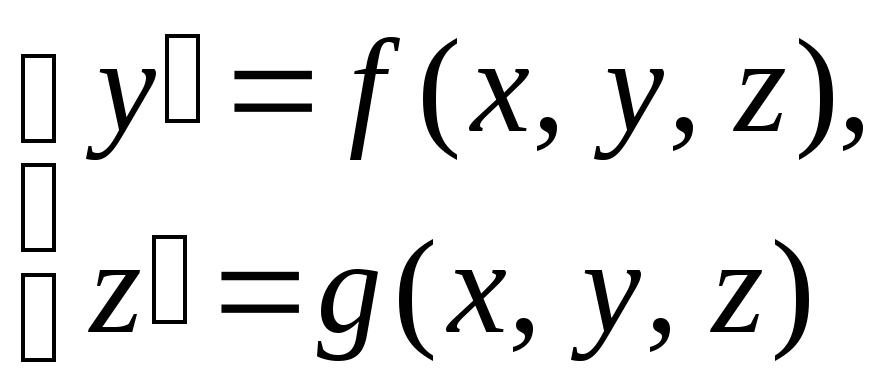
с начальными условиями формулы метода РК4 запишутся в виде

(13)

Алгоритмы одношаговых методов Рунге-Кутта

Поскольку алгоритмы одношаговых методов однотипны, то достаточно рассмотреть один пример, чтобы построить алгоритм для любого другого задания.

Методом РК3 решить систему ОДУ

Введем новые переменные Тогда система примет вид:

Используем формулы (6) для метода РК3:

Алгоритм численного интегрирования системы ОДУ представлен на рис.8.5.

Рис.8.5 – алгоритм численного интегрирования

системы ДУ методом РК3

Методы прогноза и коррекции

Для численного решения ОДУ используют также многошаговые методыв которых вычислениеведется не только поно и по значениямв нескольких предыдущих узлахФормулы- шагового метода имеют вид

где a_-q, b_-q- постоянные коэффициентыЕслисоответствующий метод называется экстраполяционным или явнымесли- интерполяционным или неявным методом

Частным случаем многошаговых методов является метод Адамса:

Обычно вычисления ведут по паре формулодна из которых явнаяа другая - неявнаяТакие пары формул называются методами прогноза и коррекцииПрогнозвыполняемый один раз на шагеслужит цели получения хорошего начального приближения для последующей коррекцииПоследняя может выполняться на каждом шаге заданное число раз (часто только один раз) или повторяться до сходимостиПрименение многошаговых методов возможно лишь в том случаеесли известны решения впервых узлахДля нахождения этих значений обычно пользуются одношаговыми методамичто увеличивает объём программыПоэтому в настоящее время многошаговые методы употребляются значительно режечем четырехточечный метод Рунге-Кутта РК4

Рассмотрим простейший вариант метода прогноза и коррекции.

Формулы метода:

(14)

По первой формуле выполняется прогноз, по второй - -я коррекция. На рис.8.4 представлена иллюстрация этого метода при=1, т.е. для первой коррекции.

Коррекцию можно выполнять сколько угодно раз; для получения решения итерационный процесс должен быть сходящимся. Условие сходимости: . Вычисления прекращаются, когдагде- заданная ошибка.

Рис.8.4 – иллюстрация метода прогноза и коррекции

Ошибки ограничения прогноза и коррекции

Представим решение в виде разложения в ряд:

.

При :

.

При :

.

Из разности получим

.

Отсюда ошибка ограничения прогноза: .

Подобным же образом можно получить ошибку ограничения коррекции:

.

Получение оценки ошибки ограничения в процессе получения решения

Пусть - точное значение решения при. Тогда

Вычтя из одного выражения другое и учитывая, что в промежутке третью производную можно считать практически постоянной, получим, откуда.

Решение на шаге получается в результате -той коррекции, и здесь же как побочный продукт вычислений можно получить оценку ошибки ограничения коррекции по выражению, которая позволяет уточнить решение:.

В заключение приведем формулы для ряда методов прогноза и коррекции (здесь - функция,- аргумент).