6. Интегральная теорема Муавра - Лапласа

Если вероятность наступления событияв каждом испытании постоянна и удовлетворяет двойному неравенству, а число независимых испытанийдостаточно велико, то вероятностьможет быть вычислена по следующей приближённой формуле

(14) ,

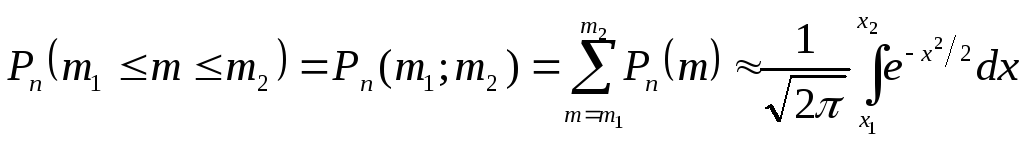где пределы интеграла определяются равенствами

Формула (14) тем точнее, чем больше число испытаний в данном эксперименте.

На основании равенство (13) формулу (14) можно переписать в виде

(15) .

Далее, введём понятие нормированной функции Лапласа:

(16) (Н.Ф.Л)

Отметим простейшие свойства функции :

Последнее свойство связано со свойствами функции Гаусса .

Функция нечётна. Действительно, после замены переменных

=;

Для проверки второго свойства достаточно сделать чертёж. Аналитически она связано с так называемым несобственным интегралом Пуассона.

Отсюда прямо следует, что для всех чисел можно полагать что,следовательно, все значения этой функции расположены в отрезке [-0,5; 0,5], при этом наименьшим являетсязатем функция медленно растёт и обращается в нуль, т.е.а затем возрастает доСледовательно, на всей числовой прямой является строго возрастающей функцией, т.е. если то

Следует отметить, что выводы свойства 2 для функции обосновывается на основании несобственного интеграла Пуассона.

Замечание.При решении задач, требующих применения интегральной теоремы Муавра-Лапласа пользуются специальными таблицами. В таблице даны значения для положительных аргументов и для; для значенийследует воспользоваться той же таблицей с учётом равенства

Далее, для того, чтобы воспользоваться таблицей функции , преобразуем равенство (15), так:

И на основании свойства 2 (нечётности ), с учётом чётности подынтегральной функции получим

=.

Таким образом, вероятность того, что событие появится внезависимых испытаниях не менеераз и не болеераз, вычисляется формулой:

(17) ;

Пример 12.Вероятность поражения мишени при одном выстреле равна 0,75. Найти вероятность того, что при 300 выстрелах мишень будет поражена не менее 150 и не более 250 раз.

Решение:Здесь,,,,. Вычисляем

,,

,.

Подставляя в интегральную формулу Лапласа, получим

.

На практике наряду с равенством (16) часто используют и другую формулу называемую «интегралом вероятности» или функцией Лапласа (см. более подробно в гл.2., п.9.,Т.9.).

(И.В. или Ф.Л.)

Для этой функции справедливы равенства:

(18) .

Следовательно, она связана с табулированной функцией и поэтому имеется также ё таблица приближённых значений (см. в конце книги, приложение).

Пример 13. Вероятность того, что деталь не прошла проверку ОТК, равна 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей непроверенных деталей окажется от 70 до 100 деталей.

Решение. По условию задачи ,,.,. Воспользуемся интегральной теоремой Муавра-Лапласа:

,

Вычислим нижний и верхний пределы интегрирования:

Следовательно, с учётом табличных значений функции ;

получим искомую вероятность

.

_{Теперь у нас есть возможность в качестве приложения рассмотренных предельных теорем доказать известную теорему «закон больших чисел в форме Бернулли»}

_.

7. Закон больших чисел (ЗБЧ в форме Бернулли)

Первым исторически самым простым законом больших чисел является теорема

Я. Бернулли. Теорема Бернулли выражает наиболее простую форму проявлния закона больших чисел. Она обосновывает теоретическую возможность приближенного вычисления вероятности события с помощью его относительной частоты, т.е. обосновывает свойство устойчивости относительной частоты.

Пусть проводится независимых испытаний, в каждом из которых вероятность наступления событияравна,а относительная частота в каждой серии испытания равна

Рассмотрим задачу:в условиях испытания по схеме Бернулли и при достаточно большом числе независимых испытаний найти вероятность отклонение относительной частоты от постоянной вероятностипоявления событияпо абсолютной величине не превышает заданного числа Другими словами, найти вероятность:

при достаточно большом числе независимых испытаний.

Теорема (ЗБЧ Я. Бернулли 1713 г.) При вышеприведённых условиях при любом , как бы ни было мало, имеет место предельное равенство

(19) .

Доказательство. Проведём доказательство этого важного утверждения на основании интегральной теоремы Муавра – Лапласа. По определению относительная частота равна

А вероятность наступления событиев одном испытании. Сначала установим следующее равенство при любоми достаточно большом:

(20) .

Действительно, в соответствии условием легко заметить, что имеет место двойное неравенство. Обозначим

(21) .

Тогда, будем иметь неравенства

.

Следовательно, для искомой вероятности . Теперь, для случаеввоспользуемся равенством

;

и с учётом нечётности получим

== 2.

Равенство (20) получено.

Из формулы (20) непосредственно следует, что при (с учётомгде), получим предельное равенство (20).

Пример 14. Вероятность того, что деталь нестандартна, равна. Найти вероятность того, что среди случайно отобранных 400 деталей относительная частота появления нестандартных деталей отклонится отпо абсолютной величине не более чем на 0,03.

Решение. Согласно условиям задачи, требуется найти

По формуле (3) имеем

=2_.

С учётом табличного значения функции получим

.

Смысл полученного результата таков: если взять достаточно большое число проб

деталей, то в каждой пробе примерно происходит отклонение относительной «частоты» на

95, 44 % и величина этих проб от вероятности, по модулю не превышающей 0,03.

Рассмотрим другой пример, где требуется найти число .

Пример 15. Вероятность того, что деталь нестандартна, равна. Сколько деталей надо отобрать, чтобы с вероятностью 0,9999 можно было бы утверждать, что относительная частота нестандартных деталей (среди отобранных), отклоняется отпо модулю не более, чем на 0,03. Найти это количество

Решение. Здесь, по условию.

Требуется определить . По формуле (13) имеем

.

Поскольку,

.

По таблице находим, что данное значение соответствует для аргумента. Отсюда,. Смысл этого результата таков: относительная частота будет заключена

между числами . Таким образом, число нестандартных деталей в 99,99 % проб будет заключено между числами 101,72 (7 % от числа 1444) и 187,72 (13 % от числа 1444).

Если взять лишь одну пробу 1444 деталей, то с большой уверенностью можно ожидать, что число нестандартных деталей будет не менее101и не более 188, в тоже время маловероятно, что их окажется меньше 101 или больше 188.

Следует заметить, что теорема Бернулли также устанавливает: при неограниченном увеличении числа испытаний частота случайного событиясходится по вероятности к истинной вероятности этого же события, т.е. справедлива оценка снизу

(22) ;,

при условии, что вероятность события от испытания к испытанию остается неизменным и равным при этом .

Неравенство (22) является прямым следствием известного неравенства Чебышева (см. далее тему «Предельные теоремы теории вероятностей» «Теорема Чебышева»). Мы позже ещё раз вернёмся к этому ЗБЧ. Оно удобно для получения оценок вероятностей снизу и двухстороннею оценку для необходимого числа наступления события, так чтобы вероятность от модуля разности относительной частоты и истинной вероятности, заданному ограничению рассматриваемого события удовлетворяло.

Пример 16.Монету подбрасывают 1000 раз. Оценить снизу вероятность отклонения частоты появления «герба» от вероятности его появления меньше чем на 0,1.

Решение. По условию здесь

На основании неравенство (4) получим

Следовательно, неравенство равносильно двойному неравенству

Поэтому можно заключить, что вероятность числа попаданий «герба» в интервал (400; 600) больше чем

_{Пример 17. В урне 1000 белых и 2000 чёрных шаров. Извлекли (с возвращением) 300 шаров. Оценить снизу вероятность того, число извлечённых шаров m (при этом они должны быть белыми) удовлетворяет двойному неравенству 80<m <120.}

_{Решение. Двойное неравенство для величины m перепишем в виде:}

_{Таким образом, требуется оценить вероятность выполнении неравенства}

Следовательно,

.

71