4. Cочетания, бином Ньютона

Пусть множество, состоящее изэлементов. Любое подмножество(включая и пустое подмножество), содержащееэлементов, называетсясочетаниемпоэлементов из (или комбинацией поэлементов из₎, при этом, разумеется,, т.е.

сочетанияминазывают комбинации, составленные изnразличных элементов поmэлементам. Сочетания считаются различными, если их состав отличаются друг от друга хотя бы одним элементом.

Теорема 2. Число сочетаний из n элементов по m определяется равенством:

(3) .

Доказательство.Пустьзаданное множество, состоящее изэлементов,- какое либо подмножество, содержащееэлементов. Составим всевозможные перестановки из элементов, получимразличных строк длиной. Если указанную операцию произвести с каждымэлементным подмножеством множества, то получим всегоразличных строк длиной. Естественно, таким способом должны получиться без исключения все строки

длиной без повторений, которые можно составить из элементов множества. Поскольку, по теореме 1, число таких строк то имеем равенство, из которого следует доказательство теоремы.Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенствами

.

т.е. с учетом равенство (2) получаем (3). В частности,

_.

Далее, рассмотрим несколько примеров на применение комбинаторных понятий.

Пример 7. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз?

Решение: Искомое число трехзначных чисел:

.

Выпишите самостоятельно эти наборы чисел.

Пример 8. Сколько можно составить сигналов из 6 флажков различного цвета, взятых

по 2?

Решение: Искомое число сигналов

.

Пример 9. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?

Решение: Искомое число способов.

Пример 10. Какое количество партий сыграли 8 шахматистов, встречаясь с каждым партнером только один раз.

Решение. В данной задаче набор пар несущественен.

Двухэлементное множество можно упорядочить только 2!=2 способами (число перестановок). Следовательно, общее число партий (пар) будет в 2! меньше, чем число размещений. Поэтому, общее число партий равно.

Решение этой задачи можно изящно иллюстрировать геометрически (см. Рис.4). Рассмотрим выпуклый восьмиугольник . С каждой любой вершины восьмиугольника можно провести к другим вершинам семь отрезков, т.е. количество встреч партий шахматистов с другими партнерами равно числу отрезков, соединяющих с остальными. Общее число вершин (шахматистов) равно 8, а так как отрезкиАВиВАи т.д. являются равными, то различных отрезков (партий) будет равно.

Задания. 1.Эту же задачу решите, с помощью турнирной таблицу встреч.

Бином Ньютона. Пустьитакие величины, для которых имеет место равенство. Из школьного курса известны алгебраические тождества:

,

,

,

,

.

Продолжая, этот процесс, т.е. пользуясь равенствами можно написать следующее равенство:

Данное равенство называется формулой бинома Ньютона. При этом мы воспользовались равенствами: =1. Неотрицательные целые числа(обычно называют их биномиальными коэффициентами) определены равенствами:

,

если ипри остальных значениях. Напомним, что принято 0!=1.

В частности, имеют место равенства:

,

Обычно формула бинома Ньютона доказывается методом математической индукции с учетом равенств:

;.

Основные свойства бинома Ньютона.

1. В разложении содержитсяслагаемых.

2. Показатель степени параметра убывает отnдо 0, напротив, показатель степенивозрастает от 0 до n, в любом случае сумма показателей степени величин (параметров)иравнаn – показателю степени бинома.

3. Биномиальные коэффициенты, равноудаленные от концов разложения, равны между собой, т.е. А также верно и другое разложение

(1)

4. Для биномиальных коэффициентов верно равенство

Некоторые непосредственные выводы.

5. Из общей формулы (1) непосредственно выводятся следующие равенства:

а. Если сумма чисел, то имеет место равенство

В дальнейшем это равенство играет важную роль в теории вероятностей.

в. Если , то сумма биномиальных коэффициентов равно, т.е. верна формула

с. Если , то сумма биномиальных коэффициентов всегда равна нулю.

.

В частности, полагая , получим равенство

.

Формулу (1) можно переписать в виде:

6. Биномиальные коэффициенты сначала возрастают, а затем, убывают. При этом:

- если показатель степени бинома четный, то биномиальный коэффициент среднего слагаемого разложения наибольший;

- если же показатель степени бинома нечетный, то биномиальные коэффициенты двух средних слагаемых равны между собой и являются наибольшими;

- на основании свойства 4.биномиальные коэффициентымогут быть вычислены с помощью так называемого «треугольника Паскаля»

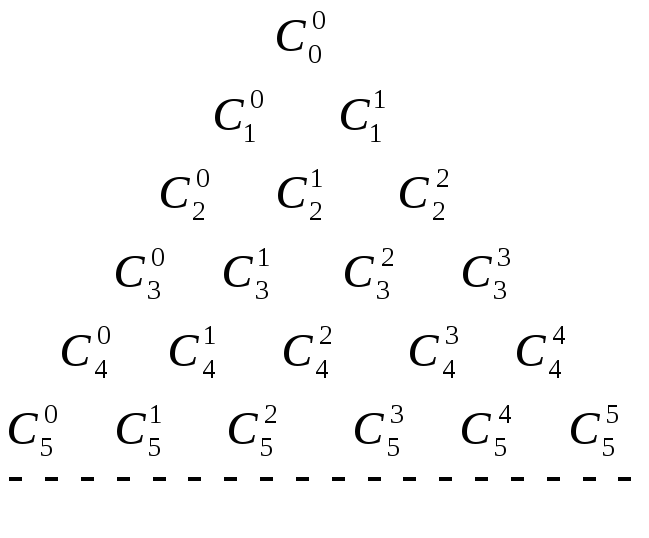
В этих «треугольных» таблицах легко заметить, что каждое число, кроме крайних единиц, является суммой двух вышерасположенных чисел.

7. Поскольку биномиальный коэффициент начинается с нулевого члена, то в общем виде принято () – ое слагаемоесчитать – им членом разложения, и обозначается:

Задача 1. Для выражениянайти шестое слагаемое.

Решение.Нужно воспользоваться биномиальной формулой, когда.

Ответ. .

Задача 2..Найдите наибольший член разложения

Решение.Для решения этой задачи необходимо выяснить для каких выполняется неравенства:

.

Рассмотрим отношение

.

Отсюда следует, что при

,

т.е., при коэффициенты убывают. Значит, для номеранаибольший член разложения бинома и он же будетдесятым слагаемым

.

Задача 3. Найти член разложения, не содержащий положительной степени(т.е. найти слагаемое содержащее).

Решение. Так как,тогда выписывая показатель степени, после несложных упрощений получим:

Следовательно, четвёртый член разложения (он же пятое слагаемое) является решением задачи.

Ниже предложим некоторые сведения из теории арифметических функций.

Упражнения: А. Докажите, что

1. При любом простом биномиальные коэффициенты делятся на число .

2. Докажите тождества:

3. , еслилюбое нечётное простое число..

В. Дополнительные сведения. Пусть - каноническое представление натурального числа, определим классическую функцию Мебиусас помощью комбинаторных коэффициентов равенством:

(**)

Докажите, что

1. Для любых взаимно простых натуральных

, (свойство мультипликативности)

2.(свойство ортогональности)

где суммирование ведётся по всем положительным целым делителям числа .

3. Вычислите функцию

Примечание. Классическая функция Мебиуса определяется несколько иначе. По этому поводу можно обратиться, например, к известным учебникам по теории чисел [3;4]. Определение (**) предложенное здесь выгодно по многим причинам. Во – первых, функция определена одной формулой, во – вторых, легко определяются различные обобщения (речь идёт о функциях

,

которая равна 0 или 1, смотря по тому, делится или не делится число натую степень числа, а также других арифметических функций, связанные с функцией Мебиуса). Подробные сведения о функции Мебиуса и её свойства можно найти в учебниках по теории чисел [3;4].

Читателям интересующихся более обстоятельно этими вопросами, рекомендуем обратиться к фундаментальным источникам по аналитической теории чисел [5-7].

Рассмотрим ещё одну тематику, обобщающую понятие размещения.

8. Размещения данного состава. Полиномиальная формула.

Начнём со следующей простой задачи

. Состав строки. Размещение данного состава. Рассмотрим наборы (строки) и. Очевидно, что они различны, но имеют один и тот же «состав» - в каждую из них входят три буквы и две буквы. Далее, уточним понятиесостава строки. Пусть некоторое членное множество, строка длиной, составленная из элементов множества. Тогда каждому номеруиз совокупности будет соответствовать число указывающее, на количество участия элементов в строке . Выписывая по порядку эти числа, получаем новую строку, которую и называют составом строки.

Например, если и , то строкаимеет следующий состав. Следовательно, в строкеэлементучаствует три раза, элементне участвует, элементучаствует два раза, элементучаствует один раз. Две строки, имеющие один и тот же состав, могут отличаться друг от друга лишь порядков элементов. Их называютразмещениями с повторениями данного состава.

Рассмотрим следующую комбинаторную задачу: найти число размещений, имеющий данный состав .

Приведём основное утверждение о числе составов

Теорема 3. Количество - различных последовательностей (составов), составленных из элементов , в которых каждый элемент встречается раз (равно

(4) .

Доказательство. Обозначим количество составов указанных в формулировке теоремы 1 буквой . А так же, положим. Введём в рассмотрениепроизвольных различных элементов:

. Для любой исходной последовательности строим различные перестановки из указанных элементов, заменяя элементы по следующему правилу. На тех местах исходной последовательности, где стояло одно и то же(этот элемент встречалсяраз), записываем какой-нибудь перестановку изэлементов . Согласно равенству (2) такое действие для одного можно осуществлять в точностиразличными способами. Проделав такое действие для каждого(), мы получим некоторую перестановку изиз указанных выше элементов. На основании формулы умножения (см. пункт) для любой последовательности строки получим всего указанным способом различных перестановок из элементов. Для различных исходных последовательностей вышеуказанным способом мы, естественно, получаем различные перестановки из взятыхэлементов. При этом любая из выбранныхэлементов может быть получена этим способом, если в качестве начальной последовательности выбрать ту строку, которая образуется в результате замены всех элементов во взятой перестановке одним элементом для кахдого. Таким образом, с учётом равенства (2) получаем:, следовательно,

И с учётом нашего обозначения , теорема доказана.

Пример 1. Количество различных 6 - значных натуральных чисел, которые можно записать с помощью цифр 1,2,3 так, чтобы каждая цифра встречалась в записи по два раза, равно:

Пример 2. В наличии имеются книги трёх наименований, причём имеется три экземпляра книг одного наименования, пять экземпляров другого и два экземпляра третьего. Количество различных размещений этих книг на одной полке составляет:

Если в наличии имеются книги различных наименований, причём поэкземпляров книг каждого наименования, то всеэкземпляров книг могут быть размещены на полке

способами.

Пример 3. В одном ряду шахматной доски располагаются: 1 король, 1 ферз, 2 слона, 2 коня, 2 ладьи. Количество всевозможных расположения этих фигур в одном ряду равно:

. Полиномиальная формула. Обобщением формулы Бинома Ньютона является так называемая полиномиальная формула, которую приведём без доказательства.

Пусть любые числа (или произвольные комутативные объекты). Имеет место

следующее утверждение

Теорема 4. Справедлива полиномиальная формула

(4)

где суммирование распространяется на всевозможные целые числа , для которых

.

Следствие.

1) Для случая , получаем формулу

(5)

2) Для случая имеет место равенство

Задания: 1. На основании равенство (5) проверьте тождество

.

2. Пусть , тогда при целомсправедливо неравенство

Это известное неравенство Бернулли.

Указание. Используйте метод математической индукции.

В завершении этого раздела сформулируем известную формулу Стирлинга без доказательства.

,

где основание натурального логарифма. Эта формула обычно применяется при больших значениях. В частности, из неё вытекает, чтос точностью доприближается выражением

.

Другими словами, справедливо (с учётом свойства логарифмической функции) неравенство