
- •Инновационный евразийский университет
- •Кафедра «Математика и информатика» Инновационный евразийский университет
- •Содержание (нужно разбить на главы после завершения)
- •Глава 1 Случайные события и их вероятности
- •Тема 1. Случайные события
- •1. Понятие испытаний, события
- •2. Виды случайных событий, пространство элементарных событий
- •3.Теоретико-множественная трактовка, алгебра событий
- •1. ;
- •Тема 2. Элементы комбинаторики и применение
- •1. Правило суммы и произведения.
- •2. Размещение с повторениями
- •3. Размещения без повторений, перестановки, подстановки
- •4. Cочетания, бином Ньютона
- •Тема 3. Определение вероятности, относительная частота, аксиоматическое определение вероятности
- •1. Классическое определение вероятности
- •2. Статистическое определение вероятности
- •3. Геометрическое определение вероятности
- •4. Аксиоматическое определение вероятности
- •5. Конечное вероятностное пространство
- •Тема 4. Теорема суммы вероятностей, формула полной системы событий, условная вероятность, теорема умножения вероятностей
- •2. Теорема умножения вероятностей
- •3. Применение комбинаторики к подсчёту вероятностей
- •4. Теоретические задачи.
- •5. Принцип практической невозможности маловероятных событий
- •Тема 5. Формула полной вероятности, вероятности гипотез,
- •1. Формула полной вероятности (фпв)
- •2. Вероятность гипотез (формулы Байеса).
- •3. Повторные испытания, схема Бернулли
- •4. Наиболее вероятностное число успехов
- •Тема 6. Предельные теоремы в схеме Бернулли,
- •1. Предельная теорема Пуассона
- •2. Простейший поток событий
- •3. Формула для геометрического закона распределения вероятности
- •5. Локальная теорема Муавра – Лапласа
- •6. Интегральная теорема Муавра - Лапласа
Тема 3. Определение вероятности, относительная частота, аксиоматическое определение вероятности
Существует простой способ определения
вероятности события, основанный на
случаях равновозможности любого из
конечного числа исходов данного испытания
(опыта в широком смысле слова). Пусть
проводится некоторый опыт с
![]() исходами, которые можно представить в
видеполной группы несовместных
равновозможныхсобытий.
исходами, которые можно представить в
видеполной группы несовместных
равновозможныхсобытий.
Такие исходы называют случаями, шансами, элементарными событиями, одним словом опыт– классическим.Обычно про такой опыт говорят, что он сводится ксхеме случаев илисхеме урн, потому, что в таких опытах вероятностную задачу, как правило, можно заменить эквивалентной ей задачей с урнами, содержащими шары разных цветов.
Случай
![]() ,
который приводит к наступлению событие
,
который приводит к наступлению событие![]() ,
называется благоприятным (или
благоприятствующим) событию.
,
называется благоприятным (или
благоприятствующим) событию.![]() ,
т.е. случай
,
т.е. случай![]() влечёт за собой событие
влечёт за собой событие![]() .
.
1. Классическое определение вероятности
Вероятностью случайного события А
называют неотрицательное
рациональное число
![]() равное отношению количества
равное отношению количества![]() -
исходов элементарных событий,
благоприятствующих событиюА,
к общему числу
-
исходов элементарных событий,
благоприятствующих событиюА,
к общему числу
![]() всех равновозможных элементарных
исходов, образующих полную группу
событий в данном опыте.
всех равновозможных элементарных
исходов, образующих полную группу
событий в данном опыте.
Обозначается это число
![]() ,или также принято использовать
обозначение
,или также принято использовать
обозначение
![]() .
.
Для величины
![]() выполняются следующие свойства:
выполняются следующие свойства:
1. Вероятность любого события
![]() заключена между нулём и единицей, т.е.
заключена между нулём и единицей, т.е.
![]() .
.
2. Вероятностьневозможногособытия равна нулю, т.е.
![]() .
.
3. Вероятностьдостоверногособытия равна единице, т.е.
![]() .
.
4. Вероятность суммы несовместных
событий равна сумме вероятностей этих
событий, т.е. если![]() ,
то
,
то
![]() .
.
Пример 1. Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра.
Решение. Пример относится к классическому определению вероятности. Обозначим через А событие – «набрана нужная цифра». Абонент мог набрать любую цифру из 10 (т.е. из 0,1,2,…,9) цифр, поэтому общее число возможных элементарных исходов равно 10.Эти исходы несовместны, равновозможные и образуют полную группу.Благоприятствует событиюАлишь один исход (нужная цифра лишь одна).
Искомая вероятность равна
![]() .
.
Пример 2. Из пяти букв разрезанной азбуки составлено слово «книга». Котёнок случайно разбросал буквы. Какова вероятность того, что пятилетний Пётр, не умеющий читать, вновь соберёт слово «книга» (событие А)?
В данном примере мы имеем с числом перестановок из пяти букв. Следовательно,
![]()
Значит, вероятность этого события равна
![]() .
.
Пример 3. Из целых чисел от 1 до 20
включительно наугад выбрали одно число.
Пусть событиеА выражает все числа,
кратные 2; событиеВ выражает все
числа, кратные 3; событиеС выражает
все числа, кратные 5; событие![]() выражает все числа, кратные 2, но среди
которых нет чисел, кратных 3 или 5;
событие
выражает все числа, кратные 2, но среди
которых нет чисел, кратных 3 или 5;
событие![]() выражает все числа, кратные 3, но среди
которых нет чисел, кратных 2 или 5;
событиеF
выражает все числа, кратные 5, но среди
которых нет чисел, кратных 2 или 3;
событие
выражает все числа, кратные 3, но среди
которых нет чисел, кратных 2 или 5;
событиеF
выражает все числа, кратные 5, но среди
которых нет чисел, кратных 2 или 3;
событие
![]() выражает все числа, некратные 2 , 3 и
5. Найти вероятности каждого события.
выражает все числа, некратные 2 , 3 и
5. Найти вероятности каждого события.
Решение. Выпишем для каждого событие благоприятствующие элементарные им события, затем находим их вероятности.
1)
![]() ;
;
2)
![]()
3)
![]()
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]()
Для любого множества
![]() символом
символом![]() (кардинальное число множества
(кардинальное число множества![]() )
будем обозначать количество элементов
этого множества. Например, в «классической
схеме» имеем:
)
будем обозначать количество элементов
этого множества. Например, в «классической
схеме» имеем:
![]()
![]()
![]() .
.
Рассмотрим классическую задачу шарами.
Задача. В ящике имеются![]() белых и
белых и![]() черных шаров. Шары тщательно перемешаны.
Наудачу извлекаются сразу два шара.
Какова вероятность того, что выбранные
шары белые?
черных шаров. Шары тщательно перемешаны.
Наудачу извлекаются сразу два шара.
Какова вероятность того, что выбранные
шары белые?
Задачу решаем с использованием элементов комбинаторики с последующим применением классического определения вероятности.
Решение.Шары можно для удобства
пронумировать от 1 до![]() общее
число шаров. Поскольку для нас неважен
порядок нумерации (какой шар первый, а
какой второй, и т.д.), то возможными
исходами опыта будут различные сочетания
из
общее
число шаров. Поскольку для нас неважен
порядок нумерации (какой шар первый, а
какой второй, и т.д.), то возможными
исходами опыта будут различные сочетания
из![]() чисел по два. Тогда общее число
чисел по два. Тогда общее число
![]() .
По условию задачи событию
.
По условию задачи событию![]() (оба
шара белые) отвечают лишь сочетания из
(оба
шара белые) отвечают лишь сочетания из![]() чисел по два, т.е.
чисел по два, т.е.![]() .
Следовательно, для искомой вероятности
на основании классической формулы
вероятности получим
.
Следовательно, для искомой вероятности
на основании классической формулы
вероятности получим
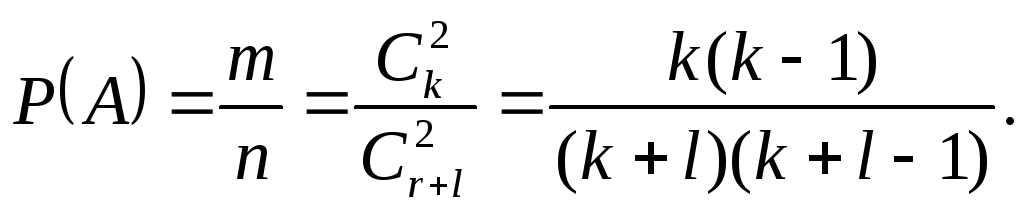
Классическое определение вероятности
применимо только для очень узкого класса
задач, где все возможные исходы опыта
можно свести к схеме случаев,
при этом![]() ,
и все событияравновозможны. В
большинстве реальных задач эта схема
неприменима. В таких ситуациях требуется
определить вероятность события иным
образом.
,
и все событияравновозможны. В
большинстве реальных задач эта схема
неприменима. В таких ситуациях требуется
определить вероятность события иным
образом.
