Частина II Диференціальне числення функцій багатьох змінних Розділ 1. Поняття дійсної функції багатьох змінних

В цьому розділі ми для функцій f, які діють з RⁿR, побудуємо апарат диференційного числення і вкажемо на деякі його застосування. Оскільки областю визначення цієї функції будуть деякі множини з простору Rⁿ, кожна точка яких задається п дійсними координатами, а значеннями цієї функції є дійсні числа, то функції, які ми будемо вивчати, називатимуться дійснозначними функціями від п дійсних змінних або функціями багатьох змінних.

Таким чином, в цьому розділі ми будемо займатися функціями виду:

f: ER¹ ERⁿ , E – область визначення функції, f(E)R – множина значень.

Графіком функції двох дійсних змінних є деяка поверхня в просторі R³. Звичайно можна ввести поняття графіка і для функції більшої кількості змінних, але тоді ця множина М буде розміщена в просторі, розмірність якого більша або рівна 4, і цей об’єкт зобразити важко.

Із попередньої частини випливає, що для функцій багатьох змінних можна вводити поняття границі і поняття неперервності. Зауважимо, що ці речі переносяться сюди.

Домовимось, окіл точки х⁽⁰⁾ , радіуса r позначати 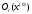, а проколотий окіл – .

Означення 1.1. (неперервність функції за Гейне). Нехай f:ER, x⁽⁰⁾E. f називається неперервною в точці х⁽⁰⁾, якщо для будь-якої послідовності {x^(к)}: x^(к)E , яка збігається до х⁽⁰⁾, послідовність {f(x^(к))} – збіжна до числа f(x⁽⁰⁾).

Означення 1.2. (неперервність функції по Коші). Нехай f: ER, x⁽⁰⁾E. Функція f називається неперервною в точці х⁽⁰⁾,якщо для будь-якого >0 існує >0 таке, що для всякого хЕ, що задовільняє нерівності (х;x⁽⁰⁾)<, виконується нерівність f(x)-f(x⁽⁰⁾)<.

Якщо х⁽⁰⁾є граничною точкою множини Е, то означення неперервності можна сформулювати наступним чином.

Означення 1.3. Нехай f: ER, x⁽⁰⁾E і х⁽⁰⁾ гранична точка множини Е. Функція f називається неперервною в точці х⁽⁰⁾, якщо .

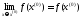Зрозуміло, що якщо f – неперервна в усіх точках множини Е, то вона називається неперервною на множині Е.

Як і для функцій однієї змінної, так і для функцій багатьох змінних мають місце теореми Вейєрштрасса. Так, як обмежена замкнена множина в просторі Rⁿ є компактом, то на основі теореми 4.4 розділу 5, першої частини дані теореми можна сформулювати наступним чином.

Теорема 1.1. (Теорема Вейєрштрасса). Якщо функція f неперервна на обмеженій і замкненій множині FRⁿ, то вона обмежена на цій множині і досягає на ній своїх найбільшого і найменшого значень.

Теорема 1.2. Якщо G відкрита і зв’язна множина в просторі Rⁿ, то будь-які дві точки цієї множини можна з’єднати неперервною кривою, всі точки якої належать множині G.

Доведення. Припустимо, що висновок теореми не вірний. Це означає, що існують дві точки х⁽¹⁾ і х⁽²⁾, які належать множині G, які не можна з’єднати неперервною кривою, всі точки якої належать множині G.

Позначимо через А множину, що містить точку х⁽¹⁾ і всі ті точки множини G, які можна з’єднати із точкою х⁽¹⁾ неперервною кривою, яка належить G. Решту точок, - позначимо через В. Тобто В=G–A.

Оскільки G – відкрита, то х⁽¹⁾ входить в G разом з деяким своїм околом. Зрозуміло, що всі точки околу можна з’єднати з центром неперервною кривою (навіть прямолінійним відрізком), тобто до А входять всі точки з околу. Це означає, що А – непорожня і відкрита множина, бо якщо якась точка х⁽³⁾А, тобто її можна зєднати з х⁽¹⁾ неперервною кривою, то неперервною кривою можна з’єднати з точкою х⁽¹⁾ всі точки з деякого околу точки х⁽³⁾.

Очевидно, що В – непорожня (бо там є х⁽²⁾) і також відкрита. Із побудови видно, що АВ=, а також , що G= AB. Оскільки множина G зв’язна, то хоча б одна з цих множин містить точку дотику другої. Нехай точка х⁽⁰⁾А є точкою дотику множини В. Тоді в будь-якому околі точки х⁽⁰⁾ є хоча б одна точка з множини В. Візьмемо окіл точки х⁽⁰⁾, який міститься в G. Всі точки з цього околу можна сполучити з х⁽⁰⁾ неперервною кривою, яка лежить в G, а значить х⁽⁰⁾ не може бути точкою дотику множини В. Аналогічно встановлюється, що жодна точка множини В не може бути точкою дотику множини А. Прийшли до суперечності. Теорему доведено.

Приклад. Нехай маємо функцію

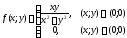
Чи буде функція неперервною в точці (0;0)? Для цього потрібно з’ясувати чи буде ?

За умовою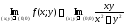. Розглянемо два шляхи прямування (x;y)(0;0).

,

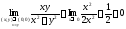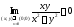, а це означає, що дана функція в даній точці границі не має. Значить в цій точці функція має розрив.

Нагадаємо, що будь-яка зв’язна відкрита множина, називаєтся областю.

Множина, що є об’єднанням області G і її граничних точок, називається замкненою областю.

Теорема1.3. (про неперервність складної функції). Нехай маємо функцію z=f(x₁, x₂,…, x_n) причому точка (х₁,...,х_п)Е, ERⁿ. Нехай задано ще таку систему функцій:

х₁=₁(t₁,…,t_k)

x₂=₂(t₁,…t_k)

.....................

x_n=_n(t₁,…,t_k),

де точки (t₁,…,t_k)GR^k. Якщо функції ₁,…,_n неперервні в точці С=(t₁⁽⁰⁾,…,t_k⁽⁰⁾)G, а функція z=f(x₁, x₂,…, x_n) неперервна в точці (х₁⁽⁰⁾,…х_п⁽⁰⁾)=х⁽⁰⁾Е (тут х₁⁽⁰⁾=₁(t₁⁽⁰⁾,…,t_k⁽⁰⁾), х₂⁽⁰⁾=₂(t₁⁽⁰⁾,…,t_k⁽⁰⁾),..., х_п⁽⁰⁾=_п(t₁⁽⁰⁾,…,t_k⁽⁰⁾)), то складна функція z від (t₁,…,t_k) – неперервна в точці t⁽⁰⁾= =(t₁⁽⁰⁾,…,t_k⁽⁰⁾).

Доведення. Оскільки функції ₁,...,_п – неперервні в точці t⁽⁰⁾,то (з означення неперервності за Гейне), для будь-якої послідовності t^(і), яка належить множині G і збіжна до t⁽⁰⁾ матимемо, що х^(і)=(х₁^(і),...,х_п^(і)) (х₁⁽⁰⁾,…х_п⁽⁰⁾). Тоді, оскільки функція f(x₁, x₂,.., x_n)= f(x) є неперервною в точці х⁽⁰⁾, то за означенням Гейне, з того, що послідовність х^(і) збігається до х⁽⁰⁾, слідує, що 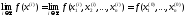, або те саме,

.

А це означає, що складна функція неперервна в точці t⁽⁰⁾. Теорему доведено.

Оскільки дана функція має множину значень, яка є деякою множиною дійсних чисел, які можна порівнювати, то виникає питання: чи має місце тут теорема Больцано-Коші?

Теорема 1.4. Больцано-Коші (для функції багатьох змінних.)

Нехай f:ER неперервна на зв’язній множині ЕRⁿ. Якщо f(x⁽¹⁾)=A, f(x⁽²⁾)=B; x⁽¹⁾, x⁽²⁾E, AB, то для будь-якої точки C,(CR), що лежить між А і В, існує точка х⁽³⁾Е така, що f(x⁽³⁾)=C.

Доведення. Оскільки Е зв’язна множина в Rⁿ, то за теоремою 1.1, будь-які дві її точки можна з’єднати неперервною кривою, всі точки якої належать множині Е. Це означає, що неперервною кривою можна з’єднати і точки х⁽¹⁾, х⁽²⁾, де х⁽¹⁾=(х₁⁽¹⁾, х₂⁽¹⁾,..., х_п⁽¹⁾), х⁽²⁾=(х₁⁽²⁾, х₂⁽²⁾,..., х_п⁽²⁾).

Таким чином існують функції х₁=₁(t), х₂=₂(t),…, х_n=_n(t), – неперервні на [,] , (₁()…_n())=x⁽¹⁾, (₁()…_n())=x⁽²⁾ і якщо t змінюється від  до , то точка рухається по цій кривій від х⁽¹⁾до х⁽²⁾.

Розглянемо нашу функцію в точках тільки цієї неперервної кривої. Оскільки точки кривої задаються системою рівнянь від змінної t, z=f(x₁, x₂,…,x_n), а точки (x₁, x₂,…,x_n) належать кривій, то х₁=₁(t), x₂=₂(t),…, x_n=_n(t). Це означає, що наша функція z є складною функцією параметра t, z=f(₁(t),₂(t),…,_n(t)), t[,]=(t) .

()=, ()=.

Оскільки f неперервна на Е, то вона неперервна в точках кривої, що належить цій множині. Кожний аргумент х_і, теж є неперервною функцією параметра t. Тому за теоремою 1.2, матимемо, що складна функція (t) є неперервною функцією однієї змінної на [, ], а звідси за теоремою Больцано-Коші (з одномірного аналізу) випливає, що існує [, ]: ()=C (з умови теореми), тобто f(₁(), ₂(),…, _n())=C, а оскільки точка (₁(), ₂(),…, _n()) є точкою нашої кривої, то вона є і точкою множини Е, позначимо її х⁽³⁾.Таким чином f(x⁽³⁾)=С. Теорему доведено.

Приведемо ще одне різницеве означення неперервності функції багатьох змінних.

Означення 1.4. Нехай U=f(x₁,…,x_n) – задана в деякій області G, і (х₁⁽⁰⁾,х₂⁽⁰⁾,...,х_п⁽⁰⁾)G. Надамо цій точці приріст, так щоб новоутворена точка не

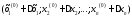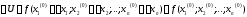вийшла за межі області G. Одержимо точку . Тоді величина, називається приростом функціїf(x₁; x₂;…;x_n).

Зрозуміло, що функція U=f(x₁,…,x_n)буде неперервною в точці (x₁⁽⁰⁾,…,x_n⁽⁰⁾) тоді і тільки тоді, коли .
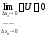