Розділ 4. Неявні функції § 1. Існування неявної функції однієї змінної

Розглнемо криву х²+у²=1, це є коло.

Зрозуміло, що якщо точка М₀ належить колу і не належить його горизонтальному діаметру, то завжди можна знайти окіл точки такий, що в ньому дане рівняння задає єдину функцію у від х, що визначена на проекції цієї дуги на вісь ОХ, тобто х, що належить проекції  у(х):х²+у(х)²=1. Будемо казати, що рівняння х²+у²=1 задає неявну функцію у від х.

Нехай функція F(x;y) визначена на множині ЕR² і Х – проекція цієї множини на вісь ОХ.

Будемо говорити, що рівняння F(x;y)=0, задає у, як функцію від х, у=f(х) на множині Х, якщо хХ існує пара (х;f(x))Е, яка задовільняє рівняння F(x;y)=0, тобто F(x;f(x))=0 є тотожністю на множині Х.

В нашому прикладі ,.

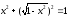Ми бачимо, що в околі точки М₀ це рівняння задаває єдину функцію у(х), щоб знайти її явне вираження, ми розв’язали наше рівняння відносно у. Та це вдасться зробити не завжди. Одже виникає така задача: як маючи певні властивості функції F, прогнозувати існування цієї неявно заданої функції, а також, які властивості повинна мати F, щоб ця неявно задана функція була, наприклад, неперервною чи диференційовною.

Зауважимо, що навіть на нашому простому прикладі видно, що якщо ми візьмемо т. М₀(1,0), то такої єдиної визначеної функції, як вище вже не буде. Якщо ми спроектуємо будь-який окіл цієї точки М₀ на ОХ, то помітимо, що на інтервалі, що належить проекції цього околу, рівняння кола задає безліч функцій у(х).

Теорема 1.1. Нехай:

1) функція F(x;y) неперервна разом із своїми частинними похідними F_x і F_y в деякому уколі т. М₀(х₀,у₀);

2) F_y в точці (x₀;y₀) не дорівнює нулю;

3) F(x₀;y₀)=0.

Тоді в деякому прямокутнику П={(x;y) x₀-₁<x<x₀+₁, y₀-₂<y<y₀+₂}, рівняння F(x;y)=0 задаватиме єдину функцію у=f(x), яка задовільняє наступним умовам:

1) ця функція буде неперервною на інтервалі (х₀-₁;x₀+₁);

2) на цьому інтервалі існує f(x), яка буде неперервною.

Доведення. Нехай . З умов 1,2 теореми випливає, що  деякий окіл т. М₀, такий, що для всіх точок М, з цього околу, F(x;y) буде диференційовною і F_y(x;y)>0

х₀-₁

У₀+₂

х₀+₁

Впишемо в цей окіл замкнений прямокутник з центром в точціМ₀ , сторони якого паралельні до координатних осей. Проведемо через т.М₀ відрізок в прямокутнику паралельний до ОУ, розглянемо функцію F_y(x;y). В точках відрізка АВ вона матиме вигляд F_y(x₀;y) (вона є похідною від функції F(x₀;y) по змінній у). Оскільки F_y(x₀;y)>0 і y₀-₂yy₀+₂, то функція F(x₀;y) є монотонно зростаючою на сегменті [y₀-₂; y₀+₂].Звідси і з того, що F(x₀, y₀)=0 одержуємо, що F(x₀, y₀-₂)<0, F(x₀;y₀+)>0 тобто, інакше кажучи, F(A)<0, F(B)>0. Так, як функція F(x,y) є неперервна в точці А і в точці В (тому що обидві ці точки належать околу де вона є неперервною), то існують окіл точки А і окіл точки В такі, що в межах першого F(x;y)<0, а другого F(x;y)>0. Не зменшуючи загальності, можна вважати, що радіуси цих околів рівні. Якщо радіус цього околу ₁ , то із вище сказаного слідує, що для будь-якого х, який належить (х₀-₁, х₀+₁), F(x,y₀-₂)<0, a F(x,y₀+₂)>0.

Візьмемо будь-яке х, яке належить (х₀-₁;х₀+₁) і проведемо через це х пряму, перпендикулярну до ОХ. Оскільки точка А лежить на відрізку А₁А₂, а в кожній точці цього відрізка F(x;y)<0, то F(A)<0. Аналогічно F(B)>0.

Розглянемо функцію F(x;y) на відрізку АВ. На цьому відрізку вона є функцією однієї змінної у (бо тут х зафіксоване). При цьому вона буде неперервною на [y₀-₂;y₀+₂] і строго зростаючою. Оскільки в лівому кінці інтервала вона приймає від’ємне значення, а в правому – додатнє, то із всього сказаного вище випливає (за теоремою Больцано-Коші), існування єдиного у із інтервала (y₀-₂;y₀+₂) такого, що F(x;y)=0.

Таким чином ми встановили, що на інтервалі (х₀-₁,х₀+₁) існує єдина функція y=f(x) така, що F(x,f(x))=0 на цьому інтервалі.

Покажемо, що функция f(x) неперервна на інтервалі (х₀-₁,х₀+₁). Нехай х(х₀-₁,х₀+₁). Дамо х приріст х. Тоді функція одержить приріст y.

Точки (x;y) і (х+х;y+y), де y=f(x), y+y=f(x+y) задовільняють рівнянню F(x;y)=0. Таким чином

F(x;y)=F(х+х;y+y)-F(x;y)=0.

Використовуючи теорему Лагранжа, одержимо:

0=F(х+х;y+y)-F(x;y)=(F(х+х;y+y)-F(x;y+y))+(F(x;y+y)-F(x;y))=

=F_x(x+x;y+y)x+F_y(x;y+₁y)y,

де 0<<1, 0<₁<1. Так, як F_y≠0, то

(1.1).

Оскільки F_x і F_y неперервні у замкнутому прямокутнику і F_y >0, то існують М>0 і т>0 такі, що  F_x ≤M і F_y>m.

Таким чином . Звідси маємо. Якщох0, то y0, а це і означає, що f(x) неперервна в точці х.

Покажемо, що існує похідна f(x) для будь-якого х(х₀-₁,х₀+₁). Нехай х(х₀-₁,х₀+₁). Надамо х приріст х. Тоді функция одержить приріст у. Якщо х0 то і у0. При цьому , де 0<<1, 0<₁<1. Враховуючи, що F_x і F_у неперервні і F_у≠0, перейшовши до границі, коли х0, одержимо:

.

А це і означає, що похідна в точці х існує і

.

Крім цього, як випливає з останньої формули,є неперервна на інтервалі(х₀-;x₀+) тому, що чисельник і знаменник останньої рівності є композиція неперервних функцій ііу=f(x). Теорему доведено.