Тема 10. Прямая, плоскость и поверхность в пространстве.
Основные вопросы темы
1.Положение плоскости в пространстве.
2.Уравнение прямой в пространстве.
3.Примеры поверхностей в пространстве.
10.1 Уравнение плоскости в пространстве.
Существуют различные методы (уравнения), определяющие положение плоскости в пространстве. Рассмотрим наиболее употребительные.
а) Общее уравнение плоскости записывается как:
Аx + Ву + Сz + D = 0.
В этом уравнении коэффициенты А, В и С определяют координаты вектора n =(А, В, С), перпендикулярного плоскости, а параметр D задает ее смещение относительно начала координат вдоль оси Оz. В частности, если плоскость проходит через начало координат, то параметр D равен нулю:
Аx + Ву + Сz = 0.
б) Нормальное уравнение плоскости. Разделив общее уравнение
плоскости на нормирующий коэффициент, равный 
A2 + B2 + C2 , получим нормальное уравнение плоскости:
x cosα + y cos β + z cosγ − p = 0 ,
где: |
cosα = |
A |
; cos β = |
B |
; cosγ = |
C |
- |
A2 + B2 +C2 |
A2 + B2 +C2 |
A2 + B2 +C2 |
направляющие косинусы вектора n ;
р – определяет расстояние от начала координат до плоскости.
в) Уравнение плоскости в отрезках: ax + by + cz = 1 ,
где: a, b, c – отрезки, отсекаемые плоскостью соответственно на осях Ox, Oy и Oz.
64
Рисунок 10.1. Иллюстрация к уравнению плоскости в отрезках.
г) Уравнение плоскости, проходящей через точку М0 (x0, y0, z0), перпендикулярно вектору n = (А, В, С), имеет вид:
А(x- x0) + В(у- у0) + С(z- z0) = 0.
Рисунок 10.2. Иллюстрация к уравнению плоскости проходящей через точку М0 (x0, y0, z0), перпендикулярно вектору n .
д) Уравнение плоскости, проходящей через три точки М1 (x1, y1, z1), М2 (x2, y2, z2) и М3 (x3, y3, z3), определяется как:
x − x1 |
y − y1 |
z − z1 |
|
|
|||
x2 − x1 |
y2 − y1 |
z2 − z1 |
= 0 |
x3 − x1 |
y3 − y1 |
z3 − z1 |
|
Некоторые частные случаи расположения плоскости в пространстве.
Различные частные случаи определяют уравнение плоскости, проходящей:
-через начало координат (x0 = у0 = z0 = 0):
Аx + Ву + Сz = 0;
-параллельно оси Ох (в этом случае в уравнении отсутствует переменная х):
Ву + Сz + D = 0;
- параллельно оси Оy (в этом случае в уравнении отсутствует переменная y):
Аx + Сz + D = 0;
65
- параллельно оси Оz (в этом случае в уравнении отсутствует переменная z):
Аx + Ву + D = 0;
- параллельно плоскости Охy (в этом случае в уравнении отсутствуют переменные х и y):
Сz + D = 0;
- параллельно плоскости Оyz (в этом случае в уравнении отсутствуют переменные y и z):
Аx + D = 0;
- параллельно плоскости Оxz (в этом случае в уравнении отсутствуют переменные х и z):
Ву + D = 0 .
Расстояние d от точки М0 (x0, y0, z0) до плоскости Аx+Ву+Сz+D=0 может быть вычислено из формулы:
d = Ax0 + By0 + Cz0 . A2 + B2 + C 2
Взаимное расположение двух плоскостей в пространстве.
Пусть две плоскости определены посредством уравнений:
А1x + В1у + С1z + D1 = 0 , А2x + В2у + С2z + D2 = 0 .
Угол φ образованный этими плоскостями может быть найден
как:
cosϕ = |
|
A1 A2 + B1B2 + C1C2 |
|
|
|
||||
A2 |
+ B2 |
+ C2 |
A2 |
+ B |
2 |
+ C2 . |
|||
|
|||||||||
1 |
1 |
1 |
2 |
2 |
2 |
|
|||
Условие параллельности двух плоскостей:
A1 = B1 = C1 .
A2 B2 C2
Условие перпендикулярности двух плоскостей:
A1 A2 + B1B2 + C1C2 = 0 .
10.2 Уравнение прямой в пространстве.
Существуют различные методы (уравнения), определяющие положение прямой в пространстве. Рассмотрим наиболее употребительные.
а) Уравнение прямой – как линии пересечения двух плоскостей:
66
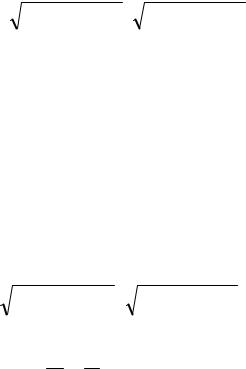
A1x + B1 y + C1z + D1 = 0
A2 x + B2 y + C2 z + D2 = 0 .
б) Уравнение прямой, проходящей через точку М1 (x1, y1, z1), с
направляющим вектором s = (m, n, p ):
|
|
x − x1 |
= |
|
y − y1 |
= |
|
z − z1 |
. |
|||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
m |
|
|
|
|
n |
|
|
|
|
p |
||||
в) Уравнение прямой, проходящей через две точки М1 (x1, y1, z1) |
||||||||||||||||||
и М2 (x2, y2, z2), определяется как: |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
x − x1 |
= |
|
y − y1 |
|
= |
z − z1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||
|
x |
2 |
− x |
|
y |
2 |
− y |
|
z |
2 |
− z |
|||||||
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
||||
Взаимное расположение двух прямых в пространстве.
Угол φ образованный между двумя прямыми, заданных вектора- |
||||||||||||
ми s1 = (m1 , n1 , p1 ) и s2 |
= (m2 , n2 , p2 ), |
может быть найден из соотно- |
||||||||||
шения: |
|
m1m2 + n1n2 + p1 p2 |
|
|
||||||||
cosϕ = ± |
|
|
. |
|||||||||
m2 + n2 + p2 m2 |
+ n2 |
+ p2 |
||||||||||
|
1 |
1 |
|
1 |
|
|
|
2 |
2 |
2 |
|
|
Условие параллельности двух прямых: |
|
|
|
|
|
|
||||||
|
|
m1 |
= |
n1 |
= |
|
p1 |
. |
|
|
|
|
|
|
m |
n |
|
p |
2 |
|
|
|
|||
|
2 |
2 |
|
|
|
|
|
|
|
|||
Условие перпендикулярности двух прямых: m1m2 + n1n2 + p1 p2 = 0 .
Взаимное расположение прямой и плоскости в пространстве.
Угол φ образованный между прямой и плоскостью может быть найден из следующего соотношения:
sin ϕ = |
|
|
Am + Bn + Cp |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
||
A2 |
+ B2 + C 2 m2 + n2 + p2 . |
||||||
|
|||||||
Условие перпендикулярности прямой и плоскости: mA = Bn = Cp .
Условие параллельности прямой и плоскости:
Am + Bn + Cp = 0 .
10.3 Примеры поверхностей в пространстве.
Приведем примеры некоторых поверхностей в пространстве.
67
68
69
Бакст Леонид Александрович
ЛИНЕЙНАЯ АЛГЕБРА
План-конспект лекционного курса
Редактор М.В. Егорова
Макет, верстка Т.А. Поверина Корректор Г.В. Платова
Лицензия ИД № 00871 от 25.01.00. Подписано в печать 10.05.2012
Формат 60×84 1/16. Усл. печ. л. 4,2. Изд. № 2363
Издательство МИЭП, типография МИЭП 105082 Москва, Рубцовская наб., д. 3, стр. 1
70