Обобщенные законы Кеплера.

Дифференциальное уравнение (2) имеет следующие первые интегралы:

Интеграл площадей

(3)

Где - постоянный вектор момента количества движения. В силу постоянства орбита тела будет являться плоской кривой. Если в этой плоскости ввести полярные координаты r и υ, то интеграл площадей можно записать в виде:

………………….. (4)

из которого следует второй закон Кеплера (закон площадей). Если –площадь, описываемая радиусом вектором за интервал времени , то секториальная скорость:

. (5)

Отсюда

(6)

Иными словами, площадь описываемая радиус – вектором, пропорциональна интервалам времени движения.

Сила, входящая в уравнение относительного движения, является потенциальной. Потенциал этой силы определяется выражением

Интеграл энергии. Из уравнения движения (2) следует закон сохранения энергии

(7)

Здесь - постоянная, равная полной механической энергии, отнесенной к массе движущегося тела.

Так как то при уравнение (7) будет выполняться для любых r, и движение не ограничено в пространстве. При ˂ 0 движение ограничено в пространстве.

В общем виде уравнение орбиты (решение уравнение (2)) имеет вид:

, (8)

где - истинная аномалия и – эксцентриситет.

Величина эксцентриситета определяется значением полной энергии и равна:

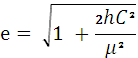. (9)

фокальный параметр равен:

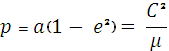(10)

Как видно из (9), возможны три вида траекторий:

1. 0 ≤ е ˂ 1 (һ˂0) - эллипс (е = 0 – окружность);

2. е = 1 (һ=0) - парабола;

3. е > 1 (һ>0)- гипербола.

Формула (8) определяет собой аналитическое выражение первого обобщенного закона Кеплера.(схема 8)

Под действием силы притяжения одно небесное тело движется в поле тяготения другого небесного тела по одному из конических сечений – кругу, эллипсу, параболе или гиперболе.

В общем случае при эллиптическом движении наиболее близкая к центральному телу точка орбиты называется перицентром, а наиболее далекая – апоцентром. При движении вокруг Солнца эти точки называются перигелием и афелием.

Третий обобщенный закон Кеплера. Для эллиптического движения легко получить связь между сидерическим периодом обращения Т и большой полуосью а орбиты. Учитывая, что площадь эллипса и радиус – вектор описывает его за период Т, имеем из (5): . С другой стороны, из (10) следует, что

…… (11)

Приравнивая эти два выражения, получим:

(12)

Это соотношение представляет собой третий обобщенный закон Кеплера. Он справедлив для любых двух притягивающихся материальных тел, будь то планеты, двойные звезды или искусственные небесные тела, ибо в правую часть соотношения (12) входят универсальные постоянные.

Пусть М₁ – масса Солнца, m₁ – масса планеты, a₁ и Т₁ – соответственно большая полуось и сидерический период обращения планеты вокруг Солнца. Если имеется другая система, например планета М₂ и спутник планеты массой m₂, который обращается вокруг планеты с периодом Т₂ на среднем расстоянии a₂, то для этих двух систем справедлив третий обобщенный закон Кеплера (12), который принимает вид:

= (13)

При движении двух тел малой массы вокруг одного центрального тела, например при движении планет вокруг Солнца, в формуле (13) следует положить М₁ = М₂, m₁ « М₁, m₂ « М₂, и тогда

то есть получаем третий эмпирический закон Кеплера.

Из выражения для эксцентриситета (9) и (11) легко найти, что

Тогда уравнение интеграла энергии (7) принимает вид:

(14)

Эта формула справедлива для любого типа движения. Для эллиптической орбиты a> 0, для параболической орбиты a = , а для гиперболической a ˂ 0.

Характеристические скорости кеплеровского движения. Для каждого расстояния rот центрального тела имеются две характерные скорости: одна при r = a – круговая скорость

(15)

имея которую, обращающееся тело движется по круговой орбите; другая – параболическая скорость

при которой движущееся тело уходит центрального тела по параболе a = . Очевидно, что всегда .

При обращении тела по эллиптической орбите средняя орбитальная скорость совпадает с круговой скоростью

(16)

где a - большая полуось орбиты и - сидерический период обращения. Из равенств (14) и (16) найдем, что в любой точке эллиптической орбиты на расстоянии r от центрального тела обращающееся тело имеет скорость

(17)

Скорость в перицентре определяется при r = q = a (1 - e),а скорость в апоцентре – при r = Q = a (1 + e).

В ограниченной задаче двух тел и определяется только массой центрального тела. Пренебрегая в первом приближении взаимным притяжением планет, можно рассматривать движение каждой из них вокруг Солнца в условиях ограниченной задачи двух тел. Тогда у любой планеты средняя скорость

. (18)

Задача двух тел

Уравнение движения

= - ( М + m )

Интеграл

площадей

=

Интеграл энергий

– = h

=

Уравнение орбиты

r =

=

= c

S = c ()

Третий

Второй

Первый

Законы Кеплера

Схема 8. Законы Кеплера