. Лекция № 4. Тема 4 : Общий случай решения систем линейных алгебраических уравнений

4.1. Ранг матрицы

Определение 1. Минором порядка k называется определитель, состо-ящий из элементов матрицы, которые находятся на пересечении k разных строк и k разных столбцов.

Определение 2. Если в матрице все миноры порядкаk > r равны нулю, а среди миноров порядка r существует, по крайней мере, один отличный от нуля, то число r называется рангом матрицы и обо-значается или.

Определение 3. Две матрицы называются эквивалентными, если одна из них получается из другой при помощи следующих преобразований:

1. Перестановка местами двух строк или столбцов матрицы;

2. Умножение всех элементов любой строки или столбца матрицы на одно и то же число, отличное от нуля;

3. Добавление ко всем элементам любой строки или столбца матрицы соответствующих элементов другой строки (столбца), умноженных на одно и то же число.

Эквивалентность матриц обозначается .

Из свойств определителей следует

Теорема 1. Все эквивалентные матрицы имеют один и тот же ранг.

Пользуясь понятием эквивалентности матриц из данной матрицы раз-мерности получают ступенчатую матрицу, т.е. матрицу вида

в которой определитель (минор r порядка)

.

а все остальные миноры порядка больше r равны нулю, так как содержат строки, состоящие из нулей.

Пример 1. Определить ранг матрицы А = .

1 шаг: Поменяем местами 1-ю и 2-ю строки;

2 шаг: Прибавим ко 2-ой строке 1-ю строку, умноженную на 2;

к 3-ей строке 1-ю строку, умноженную на 3;

к 4-ой строке 1-ю строку, умноженную на 5;

3 шаг: Прибавим к 3-ей строке 2-ю строку, умноженную на 1;

к 4-ой строке 2-ю строку, умноженную на 2;

4.2. Исследование и решение систем линейных алгебраических уравнений

Рассмотрим систему из т линейных алгебраических уравнений с п неизвестными

(1)

Решению системы (1) должно предшествовать исследование, которое приводит к следующим основным задачам теории систем линейных уравнений:

1. Определить является ли система совместной или несовместной;

2. Если система совместна, то имеет ли она единственное решение или бесконечное множество решений;

3. Если система совместна и имеет единственное решение, то найти это решение;

4. Если система совместна и имеет бесконечное множество решений, то описать всю совокупность решений.

Составим из коэффициентов системы (1) две матрицы

где А – основная матрица, а – расширенная матрица.

Ответом на первые два поставленных вопроса является

Теорема 2 (Кронекера – Капелли). Если система линейных алгебраи-ческих уравнений является совместной, то Верно и обрат-ное утверждение.

Если же система линейных алгебраических уравнений совместна, то возможны два случая:

1. Ранг матрицы А равен числу неизвестных системы, т.е. r = п.

В этом случае, отбросив уравнения-следствия, сохраняем коли-чество уравнений, равное числу неизвестных. Затем решаем полученную систему одним из известных методов.

Пример 2. Решить систему уравнений

Здесь

Определим ранг этих матриц:

1 шаг: Прибавим ко 2-ой строке 1-ю строку, умноженную на 2;

к 3-ей строке 1-ю строку;

2 шаг: Прибавим к 3-ей строке 2-ю строку, умноженную на ;

Таким образом, данная система совместна, поэтому оставляем пер-вые два уравнения и решаем полученную систему

Как видим, найденные значения неизвестных удовлетворяют и треть-ему (отброшенному) уравнению.

Замечание 1. Отметим, что можно было, например, отбросив второе уравнение, оставить первое и третье уравнение и, если эта система будет совместной, то решить полученную систему

2. Ранг матрицы А меньше числа неизвестных системы, т.е. r < п.

В этом случае, также отбрасываем уравнения-следствия, оставляя только r уравнений. Но теперь оказывается, что п  r неизвестных явля-ются свободными, т.е. не связанными никакими условиями. Вследствие этого исходная система уравнений имеет бесконечное множество решений.

Для решения такой системы оставим в левых частях уравнений системы r неизвестных с главным определителем, отличным от нуля, а все остальные члены перенесем в правые части уравнений. Затем решим полученную систему одним из известных методов, при этом выбранные r неизвестных будут выражены через п  r свободных неизвестных.

Пример 3. Решить систему уравнений

Определим ранги основной и расширенной матриц:

1 шаг: Прибавим ко 2-ой строке 1-ю строку, умноженную на 1;

к 3-ей строке 1-ю строку, умноженную на 2;

2 шаг: Прибавим к 3-ей строке 2-ю строку, умноженную на -1;

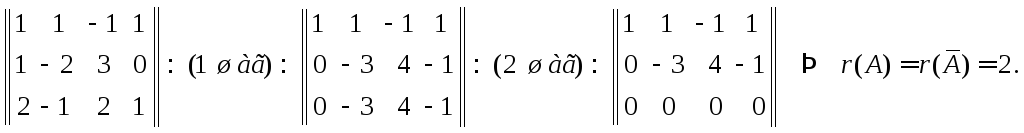
Таким образом, данная система совместна, поэтому отбрасываем третье уравнение системы и представим ее в виде

Замечание 2. Можно было представить систему и в другом виде

Нетрудно проверить, что найденные решения идентичны.