03_Электричество

Участок dS должен быть настолько малым, чтобы его можно было считать плоским, а электростатическое поле в его пределах можно было бы считать однородным.

Проведем вектор нормали n , перпендикулярный к участку dS. Вектор n - это единичный вектор

nr =1.

Проведем вектор напряженности E электростатического поля в точке пересечения силовой линии с началом вектора нормали.

Обозначим	r
α- угол между векторами n и E .

Элементарным потоком вектора напряженности электростатического по-

r

ля (вектора E ) через бесконечно малый участок поверхности называется скалярная величина

dФE = EdScosα , мВ м2 = В м.

Данное выражение можно записать иначе

EdScosα = E nrdS = E dS , dS = nrdS ,

dSr = dS,

dФE = E dS ,

где dS - вектор, модуль которого равен площади элементарного участка dS, а

направление совпадает с направлением вектора нормали n к этому участку.

r

Алгебраическая сумма элементарных потоков вектора E через все эле-

ментарные участки, на которые разбита некоторая поверхность, называется по-

r

током вектора E через эту поверхность

N r r

ФE = ∑Ei dSi . i=1

При очень большом числе слагаемых N в правой части имеем интеграл по поверхности S

ФE = ∫E dS.

S

11

В случае, если поверхность S замкнутая, то интеграл обозначается «кружочком»

ФE = ∫E dS .

S

Для замкнутой поверхности вектор нормали всегда проводят «наружу».

r

Теорема Гаусса для электростатического поля (вектора E )

Окружим точечный заряд q > 0 произвольной замкнутой поверхностью S .

Выделим на этой поверхности элемент dS , найдем элементарный поток вектора E через этот элемент.

r

r

1

q

dScosα,

dФ = E dS = EdScosα =

r2

4 πε0

dФ =

q

dScosα

=

q

dΩ,

4 πε0

4πε0

r2

dScosα =

r2 dΩ,

где dΩ- элементарный телесный угол, опирающийся на элемент поверхности dS с вершиной в точке расположения точечного заряда q .

Поток вектора E через всю поверхность S равен

12

Ф = ∫dФ = ∫

q

dΩ =

q

∫dΩ.

4πε0

4πε

0

Интеграл равен 4π и поэтому

Ф =

q

4π =

q

=

q

.

4πε0

Пусть теперь q < 0 . Тогда

ε0

ε0

dФ = EdScos(π−α)= −EdScosα = −

q

dScosα

,

4 πε0

r2

Ф = −

q

∫dΩ = −

q

=

q

.

4πε

0

ε0

ε0

В общем случае

Ф= q ,

ε0

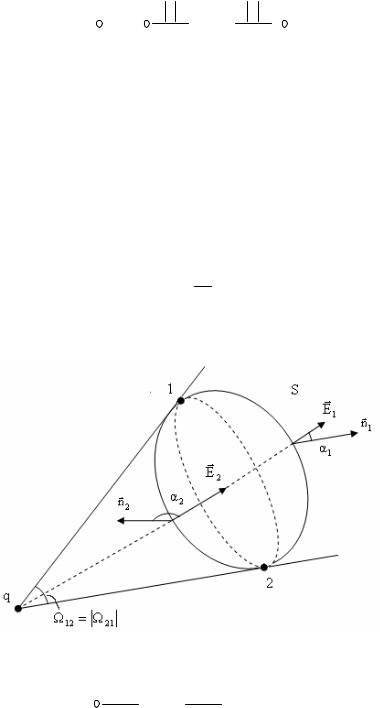
где q - алгебраическая величина заряда (с учетом знака заряда). Пусть теперь заряд q находится вне замкнутой поверхности S′.

В этом случае запишем

qq 2 1

Ф= ∫4πε0 dΩ = 4πε0 ∫1 dΩ+ ∫2 dΩ ,

	Ф =				q	(Ω12 + Ω21 ).
			4πε0				и Ω21 равны по величине и противо-
	Легко сообразить, что значения Ω12
	положны по знаку. На участке 12 углы α1						всегда меньше	π	и сosα1 > 0 , на уча-
								2
				π
	стке 21 углы α2 напротив больше				и сosα2 < 0 .
		2
	Следовательно
				Ω12 = −Ω21 ,
		Ω12 +Ω21					= 0 ,

13

Ф = 0 .

Рассмотрим теперь систему точечных зарядов. Проведем замкнутую поверхность S , которая охватывает часть точечных зарядов.

Обозначим

q1 ,q2 ,..qi ,..qn - точечные заряды, находящиеся внутри поверхности S , qn+1 ,qn+2 ,..qk ,..qm - точечные заряды вне поверхности S ,

E - напряженность поля, создаваемого всеми зарядами.

Из принципа суперпозиции

r

n

r

m

r

E = ∑Ei + ∑Ek .

i=1

k=n+1

Вычислим поток вектора E через замкнутую поверхность S .

r

r

n

r

r

m r

r

n

r

r

m

r

r

Ф = ∫E dS = ∫

∑Ei

dS +

∫ ∑Ek

dS

= ∑∫Ei dS +

∑

∫Ek dS .

S

S i=1

S k=n+1

i=1 S

k=n+1 S

Поскольку, все заряды q1 ,q2 ,..qi ,..qn

находятся внутри поверхности S , то

r

r

=

q

1 ,

∫E1

dS

S

ε0

r

r

q

∫E2

dS =

2

S

ε0

и т.д.

Первое слагаемое в правой части дает,

n	r	r	n
∑∫Ei dS = ∑q1
i=1	S		i=1	ε0

	1		n
=			∑qi
	ε	0	=
			i 1

Все заряды qn+1 ,..qk ,..qm находятся вне поверхности S , поэтому

∫En+1dS = 0 ,
S
∫En+2 dS = 0
S
и т.д.
Для второго слагаемого получим	r	r
m
∑	∫Ek dS = 0 .

k=n+1 S

14

В итоге запишем

r	r	1	n
Ф = ∫E dS =		ε0	∑qi .
S			i=1

Поток вектора E сквозь замкнутую поверхность равен алгебраической сумме зарядов внутри этой поверхности, деленной на электрическую постоянную ε0 . r

Этот результат называется теоремой Гаусса для вектора E . Теореме Гаусса можно придать следующий геометрический смысл.

Количество силовых линий, входящих в объем, ограниченный замкнутой поверхностью равно количеству силовых линий, выходящих из этого же объема.

Запишем выражение теорему Гаусса для случая непрерывного распределения заряда. В этом случае суммарный электрический заряд внутри поверхности S находится интегрированием

q = ∫ρdV ,

	V
r	r	=	1	∫ρdV .
Ф = ∫E dS
S			ε0 V

Расчет электростатического поля с помощью теоремы Гаусса

1. Заряд равномерно распределен по поверхности сферической оболочки

Заряд q равномерно распределен по поверхности сферы радиуса R , находящийся в вакууме.

15

Электростатическое поле является центрально – симметричным: направление вектора напряженности проходит через центр сферы, а величина напряженности зависит только от расстояния точки до центра сферы.

Область r ≥ R .

Проведем сферическую поверхность радиусом r > R , центр которой совпадает с центром оболочки O . Вычислим поток вектора E через эту поверхность.

∫E dS = ∫EdScosα .

S

S

Во всех точках сферы направление векторов E и n совпадают, следова-

тельно,

α = 0 ,

cosα =1 .

Кроме того, во всех точках сферы, равноудаленных от центра симметрии

модуль напряженности имеет одно и тоже значение.

r = const , E = E(r)= const ,

∫E dS = ∫E(r)dS = E(r)∫dS = E(r) 4π r2

S

S

S

∫dS = S = 4π r2 .

По теореме Гаусса

S

r

r

1

n

1

=

q ,

∫E

dS =

ε0

∑qi

ε

S

i=1

0

E(r)4πr2 =

q

,

ε0

E(r)=

q

.

		r	4πε0 r 2
	Вектор		направлен от центра, если q > 0 и к центру оболочки, если q < 0 .
		E

Область r ≤ R .

Проведем сферу радиусом r ≤ R . Предположим, что электрическое поле в этой области существует, тогда оно также будет центрально - симметричным.

16

r

Поток вектора E при этом равен

∫E dS = E(r)4π r2 .

S

По теореме Гаусса для этой же поверхности

r	r	1	n
∫E dS =		ε0	∑qi = 0 .
S			i=1

Внутри поверхности нет электрических зарядов. Следовательно,

E(r)4π r 2 = 0 , E(r)= 0 .

Электрическое поле внутри равномерно заряженной сферической оболочки отсутствует и напряженность во всех точках внутри оболочки равна нулю.

График зависимости модуля E от расстояния от центра O представлен на рисунке. В точке r = R напряженность изменяется скачком.

2. Заряд равномерно распределен по объему шара

Электрический заряд q распределен по объему шара радиусом R с постоянной объемной плотностью

ρ = const .

17

Электрическое поле в этом случае также будет центральносимметричным.

Область r ≥ R .

Проведем сферу радиусом r > R ,

центр которой совпадает с центром за-

ряженного шара. Найдем поток вектора E через эту сферу.

∫EdS = E(r)4π r2 .

S

По теореме Гаусса

q

r r

=

внутр .

∫EdS

S

ε0

Здесь qвнутр - суммарный электрический заряд внутри поверхности S .

qвнутр = ∫ρdV = ρ∫dV = ρ

4

π R 3

,

V

V

3

E(r)4π r2 =

1

ρ

4

π R 3 ,

ε0

3

4

3

π R

ρ

3

E(r) =

.

0 r 2

Обозначим

4πε

ρ

4

πR 3

= ρV = q ,

3

где q - электрический заряд шара.

Запишем

q

E(r) =

.

4πε

0 r 2

18

Область r < R .

Проведем сферическую поверхность радиусом r < R с центром в точке O .

Поток вектора E через эту поверхность равен

∫EdS = E(r)4π r2 .

S

По теореме Гаусса

r r

=

1

qвнутр ,

∫EdS

ε0

S

qвнутр = ∫ρdV = ρV

= ρ

4πr3

,

V

3

E(r)4πr2

=

1

ρ

4

πr3 ,

3

ε0

E(r) =

ρ

r

.

3ε0

График для модуля E(r) представлен на рисунке.

3. Заряд равномерно распределен по бесконечно длинной прямой ли-

нии

Электрический заряд равномерно распределен с постоянной линейной плотностью λ по длинной прямой нити.

19

Электрическое поле обладает радиальной симметрией: вектор напряженности всегда направлен вдоль прямой, перпендикулярной нити и модуль E зависит только от расстояния до нити.

Проведем поверхность S в виде прямого цилиндра радиуса r , ось которого совпадает с заряженной нитью. Обозначим высоту цилиндра h .

Вычислим поток вектора E через поверхность цилиндра

∫EdS = ∫E1dS + ∫ EdS + ∫E2dS,

S

S1

Sбок

S2

где S1 ,S2 - площадь оснований, Sбок - площадь боковой поверхности.

В каждой точке обоих оснований вектора нормали и напряженности электрического поля взаимноперпендикулярны, следовательно, первый и третий интеграл равны нулю.

∫E1dScosα1 = 0 ,

S1

∫E2 dScosα2 = 0 .

S2

Вычислим поток через боковую поверхность

∫ EdS = ∫ EdScosα = ∫ E(r)dS = E(r) ∫dS = E(r)Sбок = E(r)2π 2h .

Sбок

Sбок

Sбок

Sбок

20