03_Электричество

По теореме Гаусса

r	r	q	внутр ,
∫EdS =
S			ε0

где qвнутр - электрический заряд внутри цилиндра.

qвнутр = λ h ,

E(r)2π 2h = λ h ,

ε0

E(r) = 2πλε0 r .

4. Заряд равномерно распределен по бесконечной плоскости

Электрический заряд равномерно распределен по поверхности бесконечной плоскости с поверхностной плотностью τ = const .

Электрическое поле симметрично относительно заряженной плоскости: вектор напряженности направлен вдоль прямых, перпендикулярных плоскости; в точках удаленных от плоскости на одинаковые расстояния модуль напряженности имеет одно и тоже значение.

Построим поверхность S в виде прямого цилиндра с основаниями площадок ∆S параллельными плоскости и равноудаленными от нее.

21

Вычислим поток вектора E через поверхность цилиндра

∫EdS = ∫ E1dS + ∫ E3dS + ∫E2 dS ,

S

r

∆S1

Sбок

∆S2

∫

r

∫ E1dScosα1

= ∫E1dS = E1∆S1 ,

E1dS =

∆S1

∆S1

∆S1

∫E2 dS = E2∆S2 ,

∆S2

E1 = E2 = E(l) = E ,

∆S1 = ∆S2 = ∆S ,

r r

π

= 0 ,

∫

EdS = ∫ EdScos

2

Sбок

Sбок

∫EdS = E1∆S1 + E2∆S2

= 2E ∆S

S

= τ∆S .

qвнутр

По теореме Гаусса

r r

q

внутр ,

∫EdS =

S

ε0

2E ∆S =

τ∆S

,

ε0

E =

τ

,

2ε

0

E = const ,

E = const .

Равномерно заряженная плоскость создает однородное электростатическое поле.

5. Две параллельные равномерно заряженные бесконечные плоско-

сти

Две параллельные плоскости 1 и 2 находятся на некотором расстоянии друг от друга. Пусть на первой плоскости равномерно распределен положительный заряд с поверхностной плотностью τ.

На второй плоскости также равномерно распределен отрицательный заряд с поверхностной плоскостью − τ. Обозначим области пространства a, b, c .

Обозначим

E1 - напряженность поля, создаваемого 1-й плоскостью.

E2 - напряженность поля, создаваемого 2-й плоскостью.

E - напряженность поля, создаваемого обеими плоскостями.

22

По принципу суперпозиции:			r	r		,
	E=E1			+E2
E =	τ		,	E		=	τ	.
1	2ε	0			2		2ε0

С учетом направления векторов E1 и E2 , запишем, Область a

E= 2τε0 - 2τε0 = 0 .

Область b

E= τ + τ = τ .

2ε0 2ε0 ε0

Область c

E= 2τε0 - 2τε0 = 0 .

23

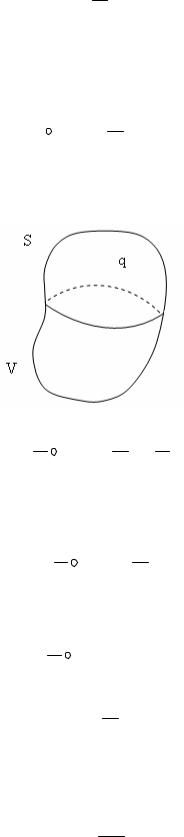
Слева и справа от заряженных плоскостей напряженность электрического поля равна нулю. В области между плоскостями электростатическое поле будет однородным, вектор напряженности направлен от положительной плоскости к отрицательной и модуль напряженности равен

E= τ .

ε0

Дифференциальная форма теоремы Гаусса

Запишем

r	r	1	q ,
∫E dS =		ε0
S

где q - суммарный заряд внутри поверхности S . Обозначим

V - объем, ограниченный замкнутой поверхностью S .

Разделим обе части равенства на V и перейдем к пределу при V → 0 .

lim

1

r

r

1

lim

q

.

V ∫

E dS =

V

V→0

ε0 V→0

При неограниченном уменьшении V правую часть можно записать так

lim

q

=

dq

=ρ

dV

V→0

V

lim

1

r

r

=

ρ

.

∫E dS

ε0

V S

r

Выражение в левой части называется дивергенцией вектора

E и обозна-

r

чается divE .

1

r

r

r

limV→0 V ∫E dS

= divE .

Итак, получили уравнение

divE=r ρ .

ε0

В общем случае

E= E(x, y,z) , ρ = ρ(x, y,z) .

Вдекартовых координатах дивергенция E имеет следующий вид

divE=r ∂∂Exx + ∂∂Eyy + ∂∂Ezz ,

24

r

где Ex ,Ey ,Ez - проекции вектора напряженности электростатического поля на оси

декартовой системы координат.

Точки поля, в которых дивергенция вектора E положительна, называется источниками поля, точки, в которых дивергенция отрицательна, называются стоками поля.

Очевидно, что источники соответствуют положительным зарядам, в которых начинаются силовые линии. Стоки соответствуют отрицательным зарядам, на которых заканчиваются силовые линии.

Запишем

r	r	1	q ,
∫E dS =		ε0
S

в случае непрерывного распределения заряда q = ∫ρdV ,

V

∫Er dSr = ∫ ρ dV ,

SV ε0

∫E dS = ∫divEdV .

S V

Данное выражение есть теорема Остроградского – Гаусса, которая справедлива и для произвольного векторного поля a

∫ar dS = ∫divar dV .

S V

Потенциальная энергия точечного заряда в электростатическом поле точечного заряда

Пусть точечный заряд q0 перемещается в электростатическом поле неподвижного точечного заряда q из точки 1 в точку 2 .

25

Найдем работу силы, действующий на заряд на всем его перемещении

r

dA=F drr ,

1

qq

0

r

,

F=

r2

4π ε0

r

dA=

1

qq0

r

drr

,

4π ε0

r2

r

rr2 =r2 ,

r

rdr=rdr ,

dA=

1

qq0

rdr

=

1

qq0

dr ,

4π ε0

r2

r

4π ε0 r2

r2

1

q q

0

q q

0

r2

dr

q q

0

1

r2

= q q

1

1

A12

=

dr

=

=

−

0

−

.

∫4πε

r2

4πε

∫r2

4πε

r

4πε

r

r

r

0

0 r

0

r

0

1

2

1

1

1

Величина A12 зависит только от положения начальной точки 1 и конечной

точки 2 и не зависит от траектории перемещения заряда между этими точками. Следовательно, силы взаимодействия между точечными зарядами являются консервативными силами.

В таком случае можно ввести потенциальную энергию заряда q0 , в электростатическом поле, создаваемом зарядом q . Обозначим ее υ.

Запишем

dA=-dυ, dA= 4qqπ ε00 drr2 ,

dυ=- 4qqπ ε00 drr2 , υ= 4π1ε0 ∫drr2 ,

υ= 4π1ε0 qqr 0 +const .

Условие нормировки потенциальной энергии точечного заряда в электростатическом поле другого заряда имеет вид

r = ∞ , υ(r = ∞) = 0 .

При этом получим

26

const=0 .

Отсюда

υ= 4π1ε0 qqr 0 , Дж

где υ - потенциальная энергия точечного заряда q0 в электростатическом поле неподвижного заряда q в точке, удаленной на расстоянии r от заряда q .

Потенциал поля точечного заряда

Потенциалом электростатического поля в некоторой точке называется скалярная величина, равная отношению потенциальной энергии точечного заряда, помещенного в эту точку, к заряду

ϕ =	υ	,	Дж	= В, Вольт.
	q0		Кл
Подставим значение υ и получим выражение для потенциала электроста-
тического поля точечного заряда q			в точке, находящейся на расстоянии r от

него

ϕ= 4π1ε0 qr , В

ϕ= 4π1ε0 εqr .

Потенциал ϕ будет положительной величиной, если q>0 и отрицательной при q<0 .

Вобщем случае потенциал является функцией координат

ϕ=ϕ(x,y,z) .

Если точечный заряд q помещен в точку поля, потенциал который равен

ϕ, то этот заряд имеет в электростатическом поле потенциальную энергию

υ= q ϕ , Дж

Потенциал электростатического поля системы точечных зарядов

Пусть точечный заряд q0 перемещается в электростатическом поле, создаваемом системой неподвижных точечных зарядов q1,q2 ,...qN . Расстояние от q0 до каждого из зарядов равно r1,r2 ,...rN . Работа, совершаемая силами такого поля над зарядом q0 равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности

N

A12 =∑A12i . i=1

Запишем

A12i =	qiq0		1	-	1	,
	4π ε0				r2i
		r1i

где r1i - расстояние от заряда qi до начальной точки 1, где находился заряд q0 ,

27

r2i - расстояние от заряда qi до конечной точки 2, куда переместился заряд

q0 .

Величина A12i не зависит от формы траектории перемещения заряда q0 , следовательно, и A12 также не зависит от пути перемещения.

Обозначим

υ- потенциальная энергия заряда q0 в поле системы точечных зарядов.

dA = −dυ,

N

N

q

i

q

0

dr

dA = ∑dAi = ∑

i

,

4πε0

2

i=1

i=1

ri

N

q

i

q

0

dr

dυ = −∑

i

4πε

r

2

i=1

0

i

N

q q

dr

N

1

q

q

i

υ = −∑i=1

i 0

∫

i

= ∑i=1

0

+ const .

4πε

r2

4πε

0

r

0

i

i

Условие нормировки: ri =∞, υ=0 . При этом получим const=0 . Тогда

υ=∑ 1

q0qi ,

N

i=1 4π ε

0

r

i

ϕ =

υ

,

q0

N

1

qi

ϕ = ∑

.

4π ε

i=1

r

0 i

Обозначим

1

qi

ϕi =

.

4π ε

0

r

i

Здесь ϕi - потенциал электростатического поля, создаваемого точечным зарядом qi в точке, находящейся на расстоянии ri от него.

Запишем

N

ϕ = ∑ϕi .

i=1

Потенциал электростатического поля системы точечных зарядов в некоторой точке равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности в той же точке.

Потенциал поля непрерывного распределения зарядов

Пусть заряд распределен в некотором пространстве с объемной плотностью ρ .

28

Обозначим (x,y,z) точку, в которой требуется определить потенциал. Возьмем произвольную точку (x′,y′,z′) и в ее окрестности построим эле-

ментарный объем:

dV=dx′dy′dz′.

Пусть dV настолько мал, что в его пределах объемная плотность посто-

янна

′

′

′

ρ(x ,y ,z )=const .

Элементарный заряд в объеме dV равен

′

′ ′

′ ′

′

′

′

′

dq=ρ(x ,y ,z

) dV=ρ(x ,y ,z )dx dy dz

Пусть объем dV настолько мал, что заряд dq можно считать точечным.

Обозначим

r - расстояние от dq до точки (x,y,z) .

Заряд dq создает в точке (x,y,z) поле с потенциалом

dϕ=

1

dq

,

4π ε0

r

где

′

2

′ 2

′ 2

.

r= (x-x )

+(y-y )

+(z-z )

Потенциал поля, создаваемого всем зарядом равен

ϕ = ∫dϕ ,

V

где V - объем, в котором распределен заряд.

ρ

(

′

′

′

)

′ ′

′

ϕ(x,y,z)=∫

1

dq

=∫

1

ρdV

=

1

∫

x ,y ,z

dx dy dz

. ( )

4π ε0

4π ε0

4π ε0

2

2

2

V

r

V

r

V

′

′

′

)

(x-x

) +(y-y ) + (z-z

Чаще всего (*) записывают в сокращенном виде

ϕ=

1

∫

ρdV

.

4π ε0 V

r

Если заряд распределен по некоторой поверхности S с поверхностной плотностью τ, то

ϕ=	1	∫	τdS	.
	4π ε0
		S r

29

В обоих случаях условие нормировки потенциала имеет вид

r → ∞ , ϕ = 0 .

Работа электростатического поля при перемещении точечного заряда

Точечный заряд q перемещается в электростатическом поле из точки 1 с потенциалом ϕ1 в точку 2 с потенциалом ϕ2 .

Работа сил поля равна убыли потенциальной энергии заряда q в этом по-

ле

A12 =υ1 -υ2 , υ1 =q ϕ1 , υ2 =q ϕ2 ,

A12 =qϕ1 −qϕ2 = q (ϕ1 −ϕ2 ), A12 = q (ϕ1 −ϕ2 ).

Величина (ϕ1 −ϕ2 ) называется разностью потенциалов точек 1 и 2.

Работа электростатического поля при перемещении точечного заряда из начальной точки в конечную точку равна произведению заряда на разность потенциалов начальной и конечной точек.

Величина (ϕ1 −ϕ2 ) имеет смысл убыли потенциала.

В случае элементарного перемещения заряда q элементарная работа сил поля равна

dA=q(-dϕ)=-qdϕ ,

30