0.4
0.3
0.2
0.1
0
-0.1
-0.2
-0.3
-0.4	-5	0	5	10
-10

Лабораторная работа № 5. Моделирование дискретных однородных марковских цепей в пакете Mathcad

Согласно теории, изложенной в п. 4.3.6, моделирование дискретных однородных марковских цепей осуществляется сравнительно легко и сводится, по сути, к моделированию дискретной случайной величины по её ряду распределения. Для осуществления самого процесса моделирования необходимо задать целый комплекс начальных условий.

Во-первых, следует сразу определить верхнюю строку табл. 4 (см. п. 4.4.6), т.е. значения всех возможных состояний марковской цепи, расположив их в таблице по возрастанию соответствующих им вероятностей. При моделировании значений дискретной марковской цепи по вычисленным по формуле (2.45) вероятностям

p j (k) можно применить метод обратной функции [23] для дис-

кретных случайных величин. Основные идеи этого метода заключаются в следующем.

Пусть имеется дискретная случайная величина ξ(ω), прини-

мающая значения

x1 ≤ x2 ≤... ≤ xk ≤...

с вероятностями

176

p1, p2 ,..., pk ,.... Её ряд распределения, очевидно, будет иметь вид , приведенный в табл. 10.

								Т а б л и ц а 10
	ξ(ω)		x1		x2	…	xk		…
	p		p1		p2	…	pk		…
	При этом интегральная функция распределения случайной ве-
личины ξ(ω) равна:
					n
		Fξ (x)=		P{ξ ≤ x}= ∑pi , xn ≤ x < xn+1, n =1,2,...,
					i=1
					Fξ (x)= 0, x < x1 .

Если γ – равномерно распределённая на (0,1) случайная величина, то случайная величина ξ(ω) получается с помощью преобра-

зования ξ = Fξ−1(γ), где Fξ−1 – функция, обратная функции распределения Fξ(x) случайной величины ξ(ω). В таком случае самый

простой алгоритм моделирования случайной величины ξ(ω) по заданному в табл. 10 ряду распределения может быть таким:

если γ < p1 , то ξ = x1 , иначе,
если γ < p1 + p2 , то ξ = x2 , иначе,
………………………………………	(4.32)

k

если γ < ∑pi , то ξ = xk , иначе,

i =1

…………………………………….

Выберем, как в двух предыдущих лабораторных работах, число различных реализаций случайного процесса n =10 , а число шагов k = 21. В этом случае вектор возможных состояний марковской цепи может быть, например, таким ξ(ω): -7, -5.5, -3.25, -2, -

1.1, 1, 2.5, 3.7, 5, 6.4. При этом выбранные значения могут располагаться в любом порядке, т.е. могут быть выстроены произвольно по возрастанию вероятностей, например так: 2.5, -7, 5, 1, -3.25, 6.4, -2, -5.5, -1.1, 3.7. Этим расположением фактически задаётся одно-

мерная функция распределения случайной величины ξ(ω).

177

Во-вторых, для однородной марковской цепи нужно задать матрицу переходных вероятностей pij , pij = const . Это квадрат-

ная матрица Pn×n , где n – число возможных состояний марков-

ской цепи. Матрица P имеет в соответствии с выбранными кон-

стантами размерность 10×10. Зададим переходные вероятности постоянными, т.е. марковская цепь будет однородной. Тогда, например,

В-третьих, зададим вектор начального распределения вероятностей: p1(0), p2 (0),..., p10 (0). Пусть начальные вероятности рас-

пределены	по усечённому геометрическому			распределению
		9		p1(0)= 0.3 ,
p(x)= pqx , x = 0,1,...,9, p(10)=1 − ∑p(i).			Тогда
p2 (0)= 0.21 ,	p3 (0)= 0.15 ,	i=1	p5 (0)= 0.07 , p6 (0)= 0.05 ,
		p4 (0)= 0.10 ,
p7 (0)= 0.04 ,	p8 (0)= 0.02 ,	p9 (0)= 0.02 ,	p10 (0)= 0.04 . Теперь есть

все данные для программы в пакете Mathcad.

178

179

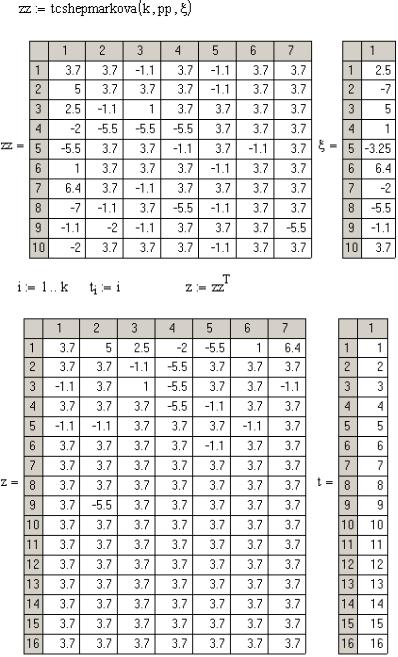
Теперь займёмся моделированием реализаций по отсчётам заданной марковской цепи. Первый столбец матрицы pp содержит

начальное распределение вероятностей, второй – вероятности состояний первого шага, т.е. первого отсчёта, третий – вероятности состояний второго отсчёта и т.д. Следует вероятности, содержащиеся в i -м столбце матрицы pp , упорядочить по возрастанию и со-

поставить с вектором ξ, содержащим по условию все возможные

состояния марковской цепи на данном шаге (в данный момент). Два этих вектора образуют ряд распределения случайной величины

ξ(ω) на данном шаге (в данный момент). По полученному ряду рас-

пределения нужно смоделировать значения состояний заданной марковской цепи на данном шаге (в данный момент или на данный отсчёт). Это можно сделать следующими подпрограммами на встроенном языке программирования пакета Mathcad:

180

181

182

Прокомментируем назначение подпрограмм на встроенном языке программирования пакета Mathcad. Подпрограмма uporjad(x) упорядочивает массив x (в данном случае это массив вероятностей) по возрастанию. Следующая подпрограмма – rjadraspred – моделирует значения случайной величины ξ(ω) по её

заданному ряду распределения по формулам (4.32). Параметр p – это вектор вероятностей, параметр x – соответствующий ему

вектор возможных значений случайной величины ξ(ω). Подпро-

грамма tcshepmarkova моделирует значения марковской цепи по шагам (времени) для различных реализаций. В результате её работы в столбцах массива xx будут содержаться все возможные значения цепи Маркова для данного отсчёта для всех вычисляемых реализаций, т.е. все значения случайной величины ξ(ω,t) для

конкретного t .

183

Подпрограмма table имеет вспомогательное значение. К сожалению, во многих случаях при неудачном задании матрицы переходных вероятностей P вероятности большинства возможных

состояний p j (k) стремятся к нулю на шагах больших значений.

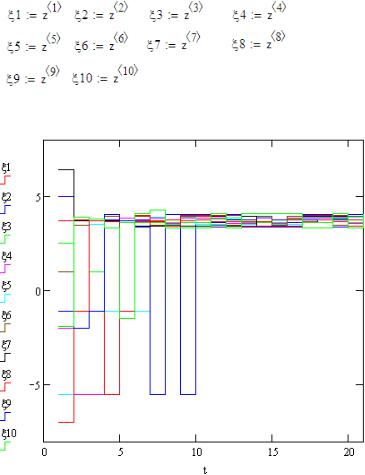
Таким образом, начиная с некоторого шага (обычно k ≈ 5 ÷ 7 ), все возможные состояния марковской цепи совпадают с наиболее вероятным значением. Это означает, что на графике реализации марковской цепи, начиная с некоторого шага k , сливаются в одну линию. Чтобы избежать этого, подпрограмма table вносит изменения в значения переменных столбцов матрицы z в размере a ε m раз,

где a – исходное значение переменной, ε – процент возможных изменений, m - число совпадений данного значения переменной в предыдущих столбцах матрицы z . Это делается лишь для того, чтобы на графике реализаций моделируемой марковской цепи значения реализаций для больших значений шагов k не сливались в одну линию (при неудачном задании матрицы переходных вероятностей P ).

184

Задание. Выбрав из приведённого задания номер варианта по номеру своей фамилии в журнале преподавателя, обратите внимание на следующее. В каждом варианте в пункте а) задаются вектор

возможных состояний марковской цепи ξ0 и отрезок X = [a,b] –

область определения всех компонент вектора возможных состояний. В эталонной программе метода (см. лаб. раб. №5) используется подпрограмма rjadraspred, моделирующая значения случайной

величины ξ(ω) по её заданному ряду распределения.

185

Однако эквивалентные значения можно смоделировать по заданной области определения методом кусочной аппроксимации (см. лаб. раб. №7) с помощью подпрограммы kusapp. Какой из этих двух методов выбрать для моделирования значений случайной величины

ξ(ω), определяет для каждого студента преподаватель, проводящий

лабораторные занятия.

В пункте б) задана матрица переходных вероятностей однородной марковской цепи P10×10 , в пункте в)– вектор начального рас-

пределения вероятностей					pp10×1	или условия, по которым он может
быть вычислен.
Вариант 1					− 0.215
					4.99
					−8.07
					0.795
а) X = [−10,5],	ξ		=		−3.51		;
		0			−9.49
					2.64
					1.55
					−5.13
					−1.04

б)

в) Начальное распределение вероятностей подчиняется биномиальному закону P(X = m)= Cnm pm (1− p)n−m с параметрами p = 0.8,n = 9 .

186

Вариант 2

			−4.02
			5.34
			−0.87
			3.12
а) X = [− 6,6], ξ			−1.91		;
	0	=
			−3.15
			0.25
			1.67
			−2.50
			4.35

б)

в) Начальное распределение вероятностей подчиняется нормальному закону с параметрами mx = −0.5,σx = 2.5 . Вероятности

состояний компонент вектора ξ0 можно вычислить с помощью

встроенной подпрограммы пакета Mathcad: dnorm. Затем непременно следует проверить выполнение условия нормировки массива pp .

187

Вариант 3

			−6.18
			−9.37
			0.15
			2.97
а) X = [−10,10], ξ			4.02		;
	0	=
			−0.06
			8.50
			−2.50
			−3.87
			9.95

б)

в) Начальное распределение вероятностей подчиняется распределению Стьюдента с двумя степенями свободы. Вероят-

ности состояний компонент вектора ξ0 можно вычислить с

помощью встроенной подпрограммы пакета Mathcad: dt. Затем непременно следует проверить выполнение условия нормировки массива pp .

188

Вариант 4

6.992.15

0.07

1.32

а) X = [0,7], ξ0 = 32..3305 ;1.07

0.69

2.75

4.95

б)

в) Начальное распределение вероятностей подчиняется распределению хи-квадрат с двумя степенями свободы. Вероятности

состояний компонент вектора ξ0 можно вычислить с помощью

встроенной подпрограммы пакета Mathcad: dchisq. Затем непременно следует проверить выполнение условия нормировки массива pp .

189

Вариант 5

			4.99
			0.0
			−2.52
			−3.12
а) X = [−4,5], ξ			3.35		;
	0	=
			1.15
			−1.09
			2.79
			−0.71
			−3.81

б)

в) Начальное распределение вероятностей подчиняется равномерному распределению, т.е. pp1,1 := pp2,1 :=...:= pp10,1 := 0.1.

190

Вариант 6

			0.07
			0.75
			1.39
			2.11
а) X = [0,5], ξ			2.95		;
	0	=
			3.48
			3.96
			4.31
			4.50
			4.89

б)

в) Начальное распределение вероятностей подчиняется распределению Фишера с тремя и четырьмя степенями свободы. Ве-

роятности состояний компонент вектора ξ0 можно вычислить с

помощью встроенной подпрограммы пакета Mathcad: dF. Затем непременно следует проверить выполнение условия нормировки массива pp .

191

Вариант 7

			−19.5
			3.75
			−15.29
			−2.11
а) X = [−20,15], ξ			−10.45		;
	0	=
			9.08
			0.25
			6.13
			−5.0
			14.86

б)

в) Начальное распределение вероятностей подчиняется нормальному закону с параметрами mx = −4,σx = 2.45 . Вероятности

состояний компонент вектора ξ0 можно вычислить с помощью

встроенной подпрограммы пакета Mathcad: dnorm. Затем непременно следует проверить выполнение условия нормировки массива pp .

192

Вариант 8

			−29.0
			0.50
			2.75
			−7.12
а) X = [−30,20], ξ			−19.64		;
	0	=
			14.22
			6.02
			−3.14
			−0.91
			19.50

б)

в) Начальное распределение вероятностей подчиняется распределению Стьюдента с тремя степенями свободы. Вероят-

ности состояний компонент вектора ξ0 можно вычислить с

помощью встроенной подпрограммы пакета Mathcad: dt. Затем непременно следует проверить выполнение условия нормировки массива pp .

193

Вариант 9

			−48.50
			31.30
			19.16
			−10.05
а) X = [−50,50], ξ			2.16		;
	0	=
			−1.83
			11.34
			−22.47
			−30.70
			49.10

б)

в) pp1,1 := 0.2 , pp2,1 := 0 , pp3,1 := 0.2 , pp4,1 := 0 , pp5,1 := 0.2 ,

pp6,1 := 0 , pp7,1 := 0.2 , pp8,1 := 0 , pp9,1 := 0.2 , pp10,1 := 0 .

194

Вариант 10

			4.90
			− 2.08
			−1.95
			−0.85
а) X = [−3,5], ξ			0.63		;
	0	=
			−0.18
			1.87
			3.11
			4.01
			−2.99

б)

в) pp1,1 := 0.5 ,	pp2,1 := 0.5 ,	pp3,1 := 0 , pp4,1 := 0 , pp5,1 := 0 ,
pp6,1 := 0 , pp7,1 := 0 ,	pp8,1 := 0 ,	pp9,1 := 0 , pp10,1 := 0 .

195

Вариант 11

			−9.89
			−7.12
			−5.21
			−3.35
а) X = [−10,0], ξ			−1.07		;
	0	=
			−0.08
			−2.11
			−4.08
			−6.34
			−8.42

б)

в) pp1,1 :=1.0 ,	pp2,1 := 0 ,	pp3,1 := 0 ,	pp4,1 := 0 , pp5,1 := 0 ,
pp6,1 := 0 , pp7,1 := 0 ,	pp8,1 := 0 ,	pp9,1 := 0 ,	pp10,1 := 0 .

196

Вариант 12

		0.09
			2.96
			6.45
			9.78
а) X = [0,15], ξ					;
	0	= 13.51
		14.85
		11.06
			8.02
			4.21
			1.57

б)

в) pp1,1 := 0.33 ,	pp2,1 := 0 ,	pp3,1 := 0 ,	pp4,1 := 0 , pp5,1 := 0.33 ,
pp6,1 := 0 , pp7,1 := 0 ,	pp8,1 := 0 ,	pp9,1 := 0 ,	pp10,1 := 0.34 .

197

Вариант 13

			−99.0
			−87.0
			−75.0
			−61.0
а) X = [−100,10], ξ			−45.0		;
	0	=
			−34.5
			−25.0
			−12.0
			0.1
			8.5

б)

в) Начальное распределение вероятностей подчиняется нормальному закону с параметрами mx = −45,σx =15. Вероятности

состояний компонент вектора ξ0 можно вычислить с помощью

встроенной подпрограммы пакета Mathcad: dnorm. Затем непременно следует проверить выполнение условия нормировки массива pp .

198

Вариант 14

			−9.85
			8.03
			−6.97
			5.48
а) X = [−10,10], ξ			−3.12		;
	0	=
			2.46
			−5.85
			7.02
			−8.15
			9.99

б)

в) pp1,1 := 0.25 ,	pp2,1 := 0 ,	pp3,1 := 0 ,	pp4,1 := 0 , pp5,1 := 0 ,
pp6,1 := 0 , pp7,1 := 0 ,	pp8,1 := 0 ,	pp9,1 := 0.35 ,	pp10,1 := 0.4 .

199

Вариант 15

			−4.82
			3.99
			2.87
			−1.95
а) X = [−5,5], ξ			−0.69		;
	0	=
			0.53
			2.03
			−3.07
			−4.01
			4.91

б)

в) pp1,1 := 0.5 ,	pp2,1 := 0 ,	pp3,1 := 0 ,	pp4,1 := 0 , pp5,1 := 0.25 ,
pp6,1 := 0 , pp7,1 := 0 ,	pp8,1 := 0 ,	pp9,1 := 0 ,	pp10,1 := 0.25 .

200