Алгоритмы C++

Задача о назначениях. Решение с помощью min-cost-flow

Задача имеет две эквивалентные постановки:

●Дана квадратная матрица A[1..N,1..N]. Нужно выбрать в ней N элементов так, чтобы в каждой строке и столбце был выбран ровно один элемент, а сумма значений этих элементов была наименьшей.

●Имеется N заказов и N станков. Про каждый заказ известна стоимость его изготовления на каждом станке. На каждом станке можно выполнять только один заказ. Требуется распределить все заказы по станкам так, чтобы минимизировать суммарную стоимость.

Здесь мы рассмотрим решение задачи на основе алгоритма нахождения потока минимальной стоимости (min-cost- flow), решив задачу о назначениях за O (N5).

Описание

Построим двудольную сеть: имеется исток S, сток T, в первой доле находятся N вершин (соответствующие строкам матрицы или заказам), во второй - тоже N вершин (соответствующие столбцам матрицы или станкам).

Между каждой вершиной i первой доли и каждой вершиной j второй доли проведём ребро с пропускной способностью 1 и стоимостью Aij. От истока S проведём рёбра ко всем вершинам i первой доли с пропускной способностью 1 и

стоимостью 0. От каждой вершины второй доли j к стоку T проведём ребро с пропускной способностью 1 и стоимостью 0.

Найдём в полученной сети максимальный поток минимальной стоимости. Очевидно, величина потока будет равна N. Далее, очевидно, что для каждой вершины i из первой доли найдётся ровно одна вершина j из второй доли, такая, что поток Fij = 1. Наконец, очевидно, это взаимно однозначное соответствие между вершинами первой доли и

вершинами второй доли является решением задачи (поскольку найденный поток имеет минимальную стоимость, то сумма стоимостей выбранных рёбер будет наименьшей из возможных, что и является критерием оптимальности).

Поскольку максимальный поток минимальной стоимости ищется за O (N3 M), то асимптотика этого решения задачи о назначениях равна O (N5).

Реализация

Приведённая здесь реализация длинноватая, возможно, её можно значительно сократить.

typedef vector<int> vint; typedef vector<vint> vvint;

const int INF = 1000*1000*1000;

int main()

{

int n;

vvint a (n, vint (n));

... чтение a ...

int m = n * 2 + 2; vvint f (m, vint (m)); int s = m-2, t = m-1; int cost = 0;

for (;;)

{

vector<int> dist (m, INF); vector<int> p (m); vector<int> type (m, 2); deque<int> q;

dist[s] = 0; p[s] = -1; type[s] = 1; q.push_back (s);

for (; !q.empty(); )

{

int v = q.front(); q.pop_front(); type[v] = 0;

if (v == s)

{

for (int i=0; i<n; ++i) if (f[s][i] == 0)

{

dist[i] = 0; p[i] = s; type[i] = 1;

q.push_back (i);

}

}

else

{

if (v < n)

{

for (int j=n; j<n+n; ++j)

if (f[v][j] < 1 && dist[j]

> dist[v] + a[v][j-n])

{

dist[j] = dist[v] + a

[v][j-n];

p[j] = v;

if (type[j] == 0) q.

push_front (j);

else if (type[j] == 2) q.push_back (j);

type[j] = 1;

}

}

else

{

for (int j=0; j<n; ++j)

if (f[v][j] < 0 && dist[j]

> dist[v] - a[j][v-n])

{

dist[j] = dist[v] - a

[j][v-n];

p[j] = v;

if (type[j] == 0) q.

push_front (j);

else if (type[j] == 2) q.push_back (j);

type[j] = 1;

}

}

}

}

int curcost = INF;

for (int i=n; i<n+n; ++i)

if (f[i][t] == 0 && dist[i] < curcost)

{

curcost = dist[i]; p[t] = i;

}

if (curcost == INF) break; cost += curcost;

for (int cur=t; cur!=-1; cur=p[cur])

{

int prev = p[cur]; if (prev!=-1)

f[cur][prev] = - (f[prev][cur] = 1);

}

}

printf ("%d\n", cost); for (int i=0; i<n; ++i)

for (int j=0; j<n; ++j)

if (f[i][j+n] == 1)

printf ("%d ", j+1);

}

Задача о назначениях. Венгерский алгоритм (алгоритм Куна) за O (N4)

Задача имеет две эквивалентные постановки:

●Дана квадратная матрица A[1..N,1..N]. Нужно выбрать в ней N элементов так, чтобы в каждой строке и столбце был выбран ровно один элемент, а сумма значений этих элементов была наименьшей.

●Имеется N заказов и N станков. Про каждый заказ известна стоимость его изготовления на каждом станке. На каждом станке можно выполнять только один заказ. Требуется распределить все заказы по станкам так, чтобы минимизировать суммарную стоимость.

Здесь рассмотрен венгерский алгоритм (изобретённый Куном), который позволяет решать задачу о назначениях очень эффективно (по сравнению с алгоритмом min-cost-flow).

Описание

[ описание пока отсутствует ]

Реализация

const int INF = 1000*1000*1000;

int n;

vector < vector<int> > a; vector<int> xy, yx; vector<char> vx, vy; vector<int> minrow, mincol;

bool dotry (int i) {

if (vx[i]) return false; vx[i] = true;

for (int j=0; j<n; ++j)

if (a[i][j]-minrow[i]-mincol[j] == 0)

vy[j] = true; for (int j=0; j<n; ++j)

if (a[i][j]-minrow[i]-mincol[j] == 0 && yx[j] == -1) { xy[i] = j;

yx[j] = i; return true;

}

for (int j=0; j<n; ++j)

if (a[i][j]-minrow[i]-mincol[j] == 0 && dotry (yx[j])) { xy[i] = j;

yx[j] = i; return true;

}

return false;

}

int main() {

... чтение a ...

mincol.assign (n, INF); minrow.assign (n, INF); for (int i=0; i<n; ++i)

for (int j=0; j<n; ++j)

minrow[i] = min (minrow[i], a[i][j]); for (int j=0; j<n; ++j)

for (int i=0; i<n; ++i)

mincol[j] = min (mincol[j], a[i][j] - minrow[i]);

xy.assign (n, -1); yx.assign (n, -1); for (int c=0; c<n; ) {

vx.assign (n, 0); vy.assign (n, 0); int k = 0;

for (int i=0; i<n; ++i)

if (xy[i] == -1 && dotry (i)) ++k;

c += k;

if (k == 0) {

int z = INF;

for (int i=0; i<n; ++i) if (vx[i])

for (int j=0; j<n; ++j) if (!vy[j])

z = min (z, a[i]

[j]-minrow[i]-mincol[j]);

for (int i=0; i<n; ++i) {

if (vx[i]) minrow[i] += z; if (vy[i]) mincol[i] -= z;

}

}

}

int ans = 0;

for (int i=0; i<n; ++i)

ans += a[i][xy[i]]; printf ("%d\n", ans);

for (int i=0; i<n; ++i)

printf ("%d ", xy[i]+1);

}

Нахождение минимального разреза. Алгоритм Штор-Вагнера

Постановка задачи

Дан неориентированный взвешенный граф		с вершинами и	рёбрами. Разрезом	называется	и
некоторое подмножество вершин (фактически, разрез — разбиение вершин на два множества: принадлежащие
все остальные). Весом разреза называется сумма весов рёбер, проходящих через разрез, т.е. таких рёбер, ровно
один конец которых	. Требуется найти разрез минимального веса.

Иногда эту задачу называют "глобальным минимальным разрезом", в отличие от задачи, когда заданы вершины-сток и исток. Глобальный минимальный разрез равен минимуму среди разрезов минимальной стоимости по

всевозможным парам исток-сток. Впрочем, как нетрудно заметить, достаточно лишь перебирать всевозможные истоки, а в качестве стока брать любую отличную вершину.

Хотя эту задачу можно решить с помощью алгоритма нахождения максимального потока (он решает неглобальную задачу минимального разреза), однако ниже описан гораздо более простой и быстрый алгоритм,

предложенный Матильдой Штор (Mechthild Stoer) и Франком Вагнером (Frank Wagner) в 1994 г.

В общем случае допускаются петли и кратные рёбра, хотя, понятно, петли абсолютно никак не влияют на результат, а все кратные рёбра можно заменить одним ребром с их суммарным весом. Поэтому мы для простоты будем считать, что во входном графе петли и кратные рёбра отсутствуют.

Описание алгоритма

Базовая идея алгоритма очень проста. Будем итеративно повторять следующий процесс: находить

минимальный разрез между какой-нибудь парой вершин	и , а затем объединять эти две вершины в одну
(соединяя списки смежности). В конце концов, после	итерации, граф сожмётся в единственную вершину и
процесс остановится. После этого ответом будет являться минимальный среди всех			найденных
разрезов. Действительно, на каждой -ой стадии найденный минимальный разрез		между вершинами и
либо окажется искомым глобальным минимальным разрезом, либо же, напротив, вершины			и невыгодно относить
к разным множествам, поэтому мы ничего не ухудшаем, объединяя эти две вершины в одну.

Таким образом, мы свели задачу к следующей: для данного графа найти минимальный разрез между какой-нибудь, произвольной, парой вершин 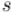и . Для решения этой задачи был предложен следующий, тоже итеративный процесс. Вводим некоторое множество вершин 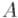, которое изначально

содержит единственную произвольную вершину. На каждом шаге находится вершина, наиболее сильно связанная с множеством 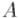, т.е. вершина 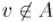, для которой следующая величина максимальна:

(т.е. сумма весов рёбер, один конец которых	, а другой принадлежит )
Опять же, этот процесс завершится через	итерацию, когда все вершины перейдут в множество	(кстати

говоря, этот процесс очень напоминает алгоритм Прима). Тогда, как утверждает теорема Штор-Вагнера, если

мы обозначим через и		последние две добавленные в		вершины, то минимальный разрез между вершинами и
будет состоять из единственной вершины — . Доказательство этой теоремы будет приведено в следующем
разделе (как это часто бывает, само по себе оно никак не способствует пониманию алгоритма).
Таким образом, общая схема алгоритма Штор-Вагнера такова. Алгоритм состоит из					фазы. На каждой
фазе множество	сначала полагается состоящим из какой-либо вершины; подсчитываются стартовые веса
вершин	. Затем происходит		итерация, на каждой из которых выбирается вершина с
наибольшим значением		и добавляется в множество , после чего пересчитываются значения

для оставшихся вершин (для чего, очевидно, надо пройтись по всем рёбрам списка смежности выбранной вершины

). После выполнения всех итераций мы запоминаем в и	номера последних двух добавленных вершин, а в
качестве стоимости найденного минимального разреза между	и можно взять значение	. Затем

надо сравнить найденный минимальный разрез с текущим ответом, если меньше, то обновить ответ. Перейти к следующей фазе.

Если не использовать никаких сложных структур данных, то самой критичной частью будет нахождение вершины

снаибольшей величиной 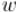. Если производить это за , то, учитывая, что всего фаз 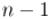, и по 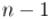итерации

вкаждой, итоговая асимптотика алгоритма получается .

Если для нахождения вершины с наибольшей величиной использовать Фибоначчиевы кучи (которые

позволяют увеличивать значение ключа за		в среднем и извлекать максимум за	в среднем), то
все связанные с множеством	операции на одной фазе выполнятся за		. Итоговая

асимптотика алгоритма в таком случае составит .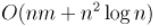

Доказательство теоремы Штор-Вагнера

Напомним условие этой теоремы. Если добавить в множество по очереди все вершины, каждый раз добавляя вершину, наиболее сильно сильно связанную с этим множеством, то обозначим предпоследнюю добавленную

вершину через 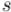, а предпоследнюю — через 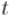. Тогда минимальный - 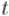разрез состоит из единственной вершины — .

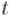Для доказательства рассмотрим произвольный	- разрез	и покажем, что его вес не может быть меньше веса
разреза, состоящего из единственной вершины	:

Для этого докажем следующий факт. Пусть		— состояние множества		на момент добавления вершины
(непосредственно перед добавлением). Пусть			— разрез множества		, индуцированный разрезом
(проще говоря,	равно пересечению этих двух множеств вершин). Далее, вершина называется активной
(по отношению к разрезу ), если вершина		и предыдущая добавленная в			вершина принадлежат разным
частям разреза . Тогда, утверждается, для любой активной вершины				выполняется неравенство:

В частности, 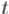является активной вершиной (т.к. перед ним добавлялась вершина 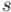), и при это неравенство превращается в утверждение теоремы:

Итак, будем доказывать неравенство, для чего воспользуемся методом математической индукции.

Для первой активной вершины 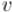это неравенство верно (более того, оно обращается в равенство) — поскольку все вершины 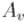принадлежат одной части разреза, а 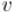— другой.

Пусть теперь это неравенство выполнено для всех активных вершин вплоть до некоторой вершины , докажем его для следующей активной вершины 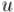. Для этого преобразуем левую часть:

Во-первых, заметим, что:

это следует из того, что когда множество	было равно	, в него была добавлена именно вершина , а не ,
значит, она имела наибольшее значение .

Далее, поскольку по предположению индукции, то получаем: