Алгоритмы C++

Алгоритм Флойда-Уоршелла нахождения кратчайших путей между всеми парами вершин

Дан ориентированный или неориентированный взвешенный граф		с вершинами. Требуется найти значения
всех величин	— длины кратчайшего пути из вершины в вершину .

Предполагается, что граф не содержит циклов отрицательного веса (тогда ответа между некоторыми парами вершин может просто не существовать — он будет бесконечно маленьким).

Этот алгоритм был одновременно опубликован в статьях Роберта Флойда (Robert Floyd) и Стивена Уоршелла (Варшалла) (Stephen Warshall) в 1962 г., по имени которых этот алгоритм и называется в настоящее время. Впрочем, в 1959 г. Бернард Рой (Bernard Roy) опубликовал практически такой же алгоритм, но его публикация

осталась незамеченной.

Описание алгоритма

Ключевая идея алгоритма — разбиение процесса поиска кратчайших путей на фазы.

Перед -ой фазой (

) считается, что в матрице расстояний

сохранены длины таких кратчайших

путей, которые содержат в качестве внутренних вершин только вершины из множества (вершины графа мы нумеруем, начиная с единицы).

Иными словами, перед -ой фазой величина

равна длине кратчайшего пути из вершины в вершину ,

если этому пути разрешается заходить только в вершины с номерами, меньшими 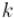(начало и конец пути не считаются). Легко убедиться, что чтобы это свойство выполнилось для первой фазы, достаточно в матрицу расстояний

записать матрицу смежности графа:

— стоимости ребра из вершины в вершину . При этом,

если между какими-то вершинами ребра нет, то записать следует величину "бесконечность" 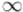. Из вершины в саму себя всегда следует записывать величину 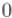, это критично для алгоритма.

Пусть теперь мы находимся на -ой фазе, и хотим пересчитать матрицу		таким образом, чтобы
она соответствовала требованиям уже для	-ой фазы. Зафиксируем какие-то вершины и . У нас возникает
два принципиально разных случая:
● Кратчайший путь из вершины в вершину	, которому разрешено дополнительно проходить через

вершины	, совпадает с кратчайшим путём, которому разрешено проходить через вершины
множества	.

В этом случае величина 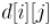не изменится при переходе с 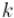-ой на 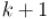-ую фазу.

●"Новый" кратчайший путь стал лучше "старого" пути.

Это означает, что "новый" кратчайший путь проходит через вершину			. Сразу отметим, что мы не потеряем
общности, рассматривая далее только простые пути (т.е. пути, не проходящие по какой-то вершине дважды).
Тогда заметим, что если мы разобьём этот "новый" путь вершиной			на две половинки (одна идущая	, а другая
—	), то каждая из этих половинок уже не заходит в вершину		. Но тогда получается, что длина каждой из
этих половинок была посчитана ещё на		-ой фазе или ещё раньше, и нам достаточно взять просто
сумму	, она и даст длину "нового" кратчайшего пути.

Объединяя эти два случая, получаем, что на -ой фазе требуется пересчитать длины кратчайших путей между всеми парами вершин 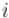и 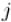следующим образом:

new_d[i][j] = min (d[i][j], d[i][k] + d[k][j]);

Таким образом, вся работа, которую требуется произвести на -ой фазе — это перебрать все пары вершин и

пересчитать длину кратчайшего пути между ними. В результате после выполнения		-ой фазы в матрице
расстояний	будет записана длина кратчайшего пути между и , либо	, если пути между этими вершинами

не существует.

Последнее замечание, которое следует сделать, — то, что можно не создавать отдельную матрицу для временной матрицы кратчайших путей на 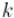-ой фазе: все изменения можно делать сразу в матрице

. В самом деле, если мы улучшили (уменьшили) какое-то значение в матрице расстояний, мы не могли ухудшить тем самым длину кратчайшего пути для каких-то других пар вершин, обработанных позднее.

Асимптотика алгоритма, очевидно, составляет		.
Реализация
На вход программе подаётся граф, заданный в виде матрицы смежности — двумерного массива			размера	,
в котором каждый элемент задаёт длину ребра между соответствующими вершинами.
Требуется, чтобы выполнялось	для любых .

for (int k=0; k<n; ++k) for (int i=0; i<n; ++i)

for (int j=0; j<n; ++j)

d[i][j] = min (d[i][j], d[i][k] + d[k][j]);

Предполагается, что если между двумя какими-то вершинами нет ребра, то в матрице смежности было записано какое-то большое число (достаточно большое, чтобы оно было больше длины любого пути в этом графе); тогда это ребро всегда будет невыгодно брать, и алгоритм сработает правильно. Правда, если не принять специальных мер, то при наличии в графе рёбер отрицательного веса, в результирующей матрице могут появиться числа вида

, , и т.д., которые, конечно, по-прежнему означают, что между соответствующими вершинами вообще нет пути. Поэтому при наличии в графе отрицательных рёбер алгоритм Флойда лучше написать так, чтобы он не выполнял переходы из тех состояний, в которых уже стоит "нет пути":

for (int k=0; k<n; ++k) for (int i=0; i<n; ++i)

for (int j=0; j<n; ++j)

if (d[i][k] < INF && d[k][j] < INF)

d[i][j] = min (d[i][j], d[i][k] + d[k][j]);

Восстановление самих путей

Легко поддерживать дополнительную информацию — так называемых "предков", по которым можно будет восстанавливать сам кратчайший путь между любыми двумя заданными вершинами в

виде последовательности вершин.

Для этого достаточно кроме матрицы расстояний

поддерживать также матрицу предков

, которая

для каждой пары вершин будет содержать номер фазы, на которой было получено кратчайшее расстояние между ними. Понятно, что этот номер фазы является не чем иным, как "средней" вершиной искомого кратчайшего пути, и

теперь нам просто надо найти кратчайший путь между вершинами и	, а также между	и .
Отсюда получается простой рекурсивный алгоритм восстановления кратчайшего пути.

Случай отрицательных циклов

Если в графе есть циклы отрицательного веса, то формально алгоритм Флойда-Уоршелла неприменим к такому графу. На самом же деле, для тех пар вершин 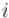и 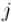, между которыми нельзя зайти в цикл отрицательного вес,

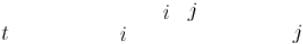
алгоритм отработает корректно.

Для тех же пар вершин, ответа для которых не существует (по причине наличия отрицательного цикла на пути между ними), алгоритм Флойда найдёт в качестве ответа какое-то число, возможно, сильно отрицательное, но

не обязательно. Тем не менее, можно улучшить алгоритм Флойда, чтобы он аккуратно обрабатывал такие пары вершин и выводил для них, например, .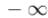

Для этого можно сделать, например, следующий критерий "не сущестования пути". Итак, пусть на данном

графе отработал обычный алгоритм Флойда. Тогда между вершинами	и не существует кратчайшего пути тогда
и только тогда, когда найдётся такая вершина , достижимая из и из	которой достижима , для которой

выполняется .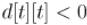

Кратчайшие пути фиксированной длины, количества путей фиксированной длины

Ниже описываются решения этих двух задач, построенные на одной и той же идее: сведение задачи к возведению матрицы в степень (с обычной операцией умножения, и с модифицированной).

Количество путей фиксированной длины

Пусть задан ориентированный невзвешенный граф с 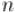вершинами, и задано целое число . Требуется для каждой пары вершин и найти количество путей между этими вершинами, состоящих ровно из рёбер. Пути при

этом рассматриваются произвольные, не обязательно простые (т.е. вершины могут повторяться сколько угодно раз).

Будем считать, что граф задан матрицей смежности, т.е. матрицей		размера	, где каждый
элемент	равен единице, если между этими вершинами есть ребро, и нулю, если ребра нет. Описываемый
ниже алгоритм работает и в случае наличия кратных рёбер: если между какими-то вершинами			и есть сразу

рёбер, то в матрицу смежности следует записать это число 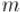. Также алгоритм корректно учитывает петли в графе, если таковые имеются.

Очевидно, что в таком виде матрица смежности графа является ответом на задачу при	—
она содержит количества путей длины между каждой парой вершин.

Решение будем строить итеративно: пусть ответ для некоторого найден, покажем, как построить его для

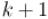. Обозначим через найденную матрицу ответов для 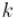, а через — матрицу ответов, которую необходимо построить. Тогда очевидна следующая формула:

Легко заметить, что записанная выше формула — не что иное, как произведение двух матриц	и в самом
обычном смысле:

Таким образом, решение этой задачи можно представить следующим образом:

Осталось заметить, что возведение матрицы в степень можно произвести эффективно с помощью алгоритма Бинарного возведения в степень.

Итак, полученное решение имеет асимптотику		и заключается в бинарном возведении в -ую
степень матрицы смежности графа.
Кратчайшие пути фиксированной длины
Пусть задан ориентированный взвешенный граф		с вершинами, и задано целое число		. Требуется для каждой
пары вершин и	найти длину кратчайшего пути между этими вершинами, состоящего ровно из рёбер.
Будем считать, что граф задан матрицей смежности, т.е. матрицей			размера	, где каждый
элемент	содержит длину ребра из вершины	в вершину . Если между какими-то вершинами ребра нет,

то соответствующий элемент матрицы считаем равным бесконечности .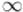

Очевидно, что в таком виде матрица смежности графа является ответом на задачу при — она содержит длины кратчайших путей между каждой парой вершин, или 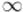, если пути длины 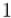не существует.

Решение будем строить итеративно: пусть ответ для некоторого найден, покажем, как построить его для

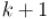. Обозначим через найденную матрицу ответов для 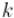, а через — матрицу ответов, которую необходимо построить. Тогда очевидна следующая формула:

Внимательно посмотрев на эту формулу, легко провести аналогию с матричным умножением: фактически, матрица 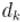умножается на матрицу 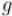, только в операции умножения вместо суммы по всем 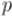берётся минимум по всем :

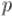где операция умножения двух матриц определяется следующим образом:

Таким образом, решение этой задачи можно представить с помощью этой операции умножения следующим образом:

Осталось заметить, что возведение в степень с этой операцией умножения можно произвести эффективно с помощью алгоритма Бинарного возведения в степень, поскольку единственное требуемое для него свойство

— ассоциативность операции умножения — очевидно, имеется.

Итак, полученное решение имеет асимптотику

и заключается в бинарном возведении в -ую

степень матрицы смежности графа с изменённой операцией умножения матриц.

Минимальное остовное дерево. Алгоритм Прима

Дан взвешенный неориентированный граф. Требуется найти такое поддерево этого графа, которое бы соединяло все его вершины, и при этом обладало наименьшим весом (т.е. суммой весов рёбер) из всех возможных. Такое поддерево называется минимальным остовным деревом или простом минимальным остовом.

Здесь будут рассмотрены несколько важных фактов, связанных с минимальными остовами, затем будет рассмотрен алгоритм Прима в его простейшей реализации, а затем слегка улучшенный вариант.

Свойства минимального остова

●Минимальный остов уникален, если веса всех рёбер различны. В противном случае, может существовать несколько минимальных остовов (конкретные алгоритмы обычно получают один из возможных остовов).

●Минимальный остов является также и остовом с минимальным произведением весов рёбер. (доказывается это легко, достаточно заменить веса всех рёбер на их логарифмы)

●Минимальный остов является также и остовом с минимальным весом самого тяжелого ребра. (это утверждение следует из справедливости алгоритма Крускала)

●Остов максимального веса ищется аналогично остову минимального веса, достаточно поменять знаки всех рёбер на противоположные и выполнить любой из алгоритм минимального остова.

Алгоритм Прима

Этот алгоритм был описан в статье Прима (Prim) в 1957 г., хотя этот алгоритм был открыт ещё в 1930 г. Ярником (Jarnik). Алгоритм Прима постепенно строит искомый минимальный остов, добавляя в него по одному ребру на каждом шаге.

(Это означает, что алгоритм Прима является жадным. Более того, справедливость алгоритма Прима легко устанавливается в рамках теории матроидов.)

В начале работы алгоритма результирующее дерево состоит из одной вершины (её можно выбирать произвольно).

Алгоритм состоит из N-1 итерации, на каждой из которой к дереву добавляется ровно одно ребро, не нарушающее свойства дерева (т.е. один конец добавляемого ребра принадлежит дереву, а другой - не принадлежит). Ключевой момент - из всех таких рёбер каждый раз выбирается ребро с минимальным весом.

Простейшая реализация

Этот код самым непосредственным образом реализует описанный выше алгоритм, и выполняется за O (N M).

int n;

vector < vector < pair<int,int> > > g; // пары вершина-вес

... чтение графа ...

vector<char> used (n); used[0] = true;

vector < pair<int,int> > result; for (int i=0; i<n-1; ++i)

{

int minv = -1; size_t minr; for (int j=0; j<n; ++j)

if (used[j])

for (size_t k=0; k<g[j].size(); ++k) if (!used [ g[j][k].first ])

if (minv == -1 || g[j][k].second <

g[minv][minr].second)

minv = j, minr = k;

used [ g[minv][minr].first ] = true;

result.push_back (make_pair (minv, g[minv][minr].first));

}

cout << "Result (all ribs):\n"; for (int i=0; i<n-1; ++i)

cout << result[i].first << ' ' << result[i].second << '\n';

Улучшенная реализация

Эта реализация будет выполняться заметно быстрее - за O (M log N + N2).

Для этого мы отсортируем все рёбра в списках смежности каждой вершины по увеличению веса (потребуется O (M log M) = O (M log N)). Кроме того, для каждой вершины заведем указатель, указывающий на первое доступное ребро в её списке смежности. Изначально все указатели указывают на начала списков, т.е. равны 0. На i-ой итерации

алгоритма Прима мы перебираем все вершины, и выбираем наименьшее по весу ребро среди доступных. Поскольку всё рёбра уже отсортированы по весу, а указатели указывают на первые доступные рёбра, то выбор наименьшего ребра осуществится за O (N). Теперь нам следует обновить указатели, посколько некоторые из них указывают на

ставшие недоступными рёбра (оба конца которых оказались внутри дерева), т.е. сдвинуть некоторые из них

вправо. Однако, поскольку во всех списках смежности в сумме 2 * M элементов, а указатели сдвигаются только вправо, то получается, что на поддержание всех указателей потребуется O (M) действий. Итого - время выполнения алгоритма

O (M log M + N2 + M), т.е. O (M log N + N2).

int n;

vector < vector < pair<int,int> > > g; // пары вес-вершина

... чтение графа ...

for (int i=0; i<n; ++i)

sort (g[i].begin(), g[i].end());

vector<char> used (n); used[0] = true;

vector < pair<int,int> > result; vector<size_t> ptr (n);

for (int i=0; i<n-1; ++i)

{

int minv = -1;

for (int j=0; j<n; ++j) if (used[j])

if (ptr[j] < g[j].size())

if (minv == -1 || g[j][ptr[j]].first < g

[minv][ptr[minv]].first)

minv = j; used [ g[minv][ptr[minv]].second ] = true;

result.push_back (make_pair (minv, g[minv][ptr[minv]].second)); for (int j=0; j<n; ++j)

while (ptr[j] < g[j].size() && used [ g[j][ptr[j]].second ]) ++ptr[j];

}

cout << "Result (all ribs):\n"; for (int i=0; i<n-1; ++i)

cout << result[i].first << ' ' << result[i].second << '\n';