Алгоритмы C++

for (size_t j=0; j<g[v].size(); ++j) { int to = g[v][j].first,

len = g[v][j].second; if (d[v] + len < d[to]) {

q.erase (make_pair (d[to], to)); d[to] = d[v] + len;

p[to] = v;

q.insert (make_pair (d[to], to));

}

}

}

}

В отличие от обычного алгоритма Дейкстры, становится ненужным массив			. Его роль, как и функцию
нахождения вершины с наименьшим расстоянием, выполняет	. Изначально в него помещаем стартовую вершину
с её расстоянием. Основной цикл алгоритма выполняется, пока в очереди есть хоть одна вершина. Из
очереди извлекается вершина с наименьшим расстоянием, и затем из неё выполняются релаксации. Перед
выполнением каждой успешной релаксации мы сначала удаляем из		старую пару, а затем, после

выполнения релаксации, добавляем обратно новую пару (с новым расстоянием ).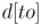

priority_queue

Принципиально здесь отличий от

нет, за исключением того момента, что удалять из

произвольные элементы невозможно (хотя теоретически кучи поддерживают такую операцию, в стандартной библиотеке она не реализована). Поэтому приходится совершать "обходной манёвр": при релаксации просто не будем удалять старые пары из очереди. В результате в очереди могут находиться одновременно несколько пар для одной и той же вершины (но с разными расстояниями). Среди этих пар нас интересует только одна, для которой

элемент

равен

, а все остальные являются фиктивными. Поэтому надо сделать небольшую модификацию:

в начале каждой итерации, когда мы извлекаем из очереди очередную пару, будем проверять, фиктивная она или нет (для этого достаточно сравнить 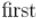и ). Следует отметить, что это важная модификация: если не сделать её, то

это приведёт к значительному ухудшению асимптотики (до ).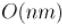

Ещё нужно помнить о том, что

упорядочивает элементы по убыванию, а не по возрастанию,

как обычно. Проще всего преодолеть эту особенность не указанием своего оператора сравнения, а просто помещая в качестве элементов расстояния со знаком минус. В результате в корне кучи будут оказываться элементы с наименьшим расстоянием, что нам и нужно.

const int INF = 1000000000;

int main() { int n;

... чтение n ...

vector < vector < pair<int,int> > > g (n);

... чтение графа ...

int s = ...; // стартовая вершина

vector<int> d (n, INF), p (n); d[s] = 0;

priority_queue < pair<int,int> > q; q.push (make_pair (0, s));

while (!q.empty()) {

int v = q.top().second, cur_d = -q.top().first; q.pop();

if (cur_d > d[v]) continue;

for (size_t j=0; j<g[v].size(); ++j) { int to = g[v][j].first,

len = g[v][j].second; if (d[v] + len < d[to]) {

d[to] = d[v] + len; p[to] = v;

q.push (make_pair (-d[to], to));

}

}

}

}

Как правило, на практике версия с 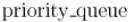оказывается несколько быстрее версии с .

Избавление от pair

Можно ещё немного улучшить производительность, если в контейнерах всё же хранить не пары, а только номера вершин. При этом, понятно, надо перегрузить оператор сравнения для вершин: сравнивать две вершины надо по расстояниям до них .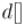

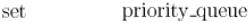
Поскольку в результате релаксации величина расстояния до какой-то вершины меняется, то надо понимать, что "сама по себе" структура данных не перестроится. Поэтому, хотя может показаться, что удалять/добавлять элементы в контейнер в процессе релаксации не надо, это приведёт к разрушению структуры данных. По-прежнему перед релаксацией надо удалить из структуры данных вершину 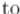, а после релаксации вставить её обратно — тогда никакие соотношения между элементами структуры данных не нарушатся.

А поскольку удалять элементы можно из

, но нельзя из

, то получается, что этот приём

применим только к 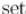. На практике он заметно увеличивает производительность, особенно когда для хранения расстояний используются большие типы данных (как 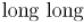или ).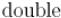

Алгоритм Форда-Беллмана

С помощью алгоритма Форда-Беллмана можно найти кратчайшие пути между заданной вершиной и всеми остальными вершинами за O (N M).

В отличие от алгоритма Дейкстры, этот алгоритм применим и к графам, содержащим отрицательные рёбра. Впрочем,

если граф содержит отрицательный цикл, то, понятно, результат алгоритма будет неопределён (несмотря на это, алгоритм успешно используется при решении задачи "Отрицательный цикл").

Алгоритм

Пусть массив D - результирующий массив, который будет вычислен окончательно к концу алгоритма. Пусть также N - число вершин, S - номер стартовой вершины. Сначала заполним D значениями "бесконечность" (например, миллиард), за исключением стартовой вершины, в которой D[S] = 0. Выполним N-1 итерацию алгоритма, в каждой из которых будем пытаться улучшить ответ - уменьшить значения в массиве. Для этого мы просто перебираем все рёбра и каждым ребром пробуем улучшить длину пути. После выполнения всех N-1 итераций, массив D будет содержать искомые значения (если, конечно, граф не содержит отрицательных циклов).

Реализация

Код, выполняющий алгоритм Форда-Беллмана из вершины 1:

typedef pair<int,int> rib; typedef vector<rib> graph_line;

typedef graph_line::iterator graph_iter; typedef vector<graph_line> graph;

const int inf = 1000*1000*1000;

int main()

{

int n; graph g;

... чтение графа ...

vector<long long> d (n, inf); d[0] = 0;

vector<int> from (n, -1); from[0] = 0;

for (int count=1; count<n; count++)

{

bool anychanged = false; for (int v=0; v<n; v++)

if (d[v] != inf)

for (graph_iter i=g[v].begin(); i!=g[v].end();

++i)

{

int to = i->first, l = i->second; if (d[to] > d[v]+l)

{

d[to] = d[v]+l; from[to] = v; anychanged = true;

}

}

if (!anychanged) break;

}

... вывод массива d ...

}

Во-первых, этот код использует небольшую оптимизацию алгоритма: все N-1 итерации не обязательно выполняются, если обнаружено, что уже на каком-то более раннем шаге ответ уже получен. Действительно, если на некотором шаге мы не улучшили D ни в одной вершине, то, очевидно, и все последующие итерации ничего не смогут

улучшить. Следовательно, можно остановить алгоритм прямо на этом шаге. На самом деле, эта оптимизация в некоторых случаях позволяет очень существенно снизить время работы алгоритма.

Во-вторых, представленный код строит не только массив расстояний D, но и массив предков from. По окончании работы алгоритма в каждом элементе from[i] будет содержаться "предок" вершины i, т.е. from[i] - это вершина, из

которой мы пришли в вершину i, двигаясь по кратчайшему пути. Следовательно, имея массив from, мы можем теперь и восстановить собственно путь до любой вершины:

int v = n-1; // это вершина, путь до которой нам нужно вывести. например, n-1 vector<int> path;

while (true)

{

path.push_back (v);

if (v == from[v]) break; v = from[v];

}

reverse (path.begin(), path.end()); // путь получится сначала задом наперёд for (size_t i=0; i<path.size(); ++i)

cout << path[i] << ' ';

Алгоритм Левита нахождения кратчайших путей

от заданной вершины до всех остальных вершин за O (N M)

Пусть дан граф с N вершинами и M ребрами, для каждого из которых указан его вес Li. Также дана стартовая вершина V0. Требуется найти кратчайшие пути от вершины V0 до всех остальных вершин.

Алгоритм Левита решает эту задачу весьма эффективно (по поводу асимптотики и скорости работы см. ниже).

Описание

Пусть массив D[1..N] будет содержать текущие кратчайшие длины путей, т.е. Di - это текущая длина кратчайшего пути от вершины V0 до вершины i. Изначально массив D заполнен значениями "бесконечность", кроме DV0 = 0. По

окончании работы алгоритма этот массив будет содержать окончательные кратчайшие расстояния.

Пусть массив P[1..N] содержит текущих предков, т.е. Di - это вершина, предшествующая вершине i в кратчайшем пути от вершины V0 до i. Так же как и массив D, массив P изменяется постепенно по ходу алгоритма и к концу его принимает окончательные значения.

Теперь собственно сам алгоритм Левита. На каждом шаге поддерживается три множества вершин:

●M0 - вершины, расстояние до которых уже вычислено (но, возможно, не окончательно);

●M1 - вершины, расстояние до которых вычисляется;

●M2 - вершины, расстояние до которых ещё не вычислено.

Вершины в множестве M1 хранятся в виде двунаправленной очереди (deque).

Изначально все вершины помещаются в множество M2, кроме вершины V0, которая помещается в множество M1.

На каждом шаге алгоритма мы берём вершину из множества M1 (достаём верхний элемент из очереди). Пусть V -

это выбранная вершина. Переводим эту вершину во множество M0. Затем просматриваем все рёбра, выходящие из этой вершины. Пусть T - это второй конец текущего ребра (т.е. не равный V), а L - это длина текущего ребра.

●Если T принадлежит M2, то T переносим во множество M1 в конец очереди. DT полагаем равным DV + L.

●Если T принадлежит M1, то пытаемся улучшить значение DT: DT = min (DT, DV + L). Сама вершина T никак не передвигается в очереди.

●Если T принадлежит M0, и если DT можно улучшить (DT > DV + L), то улучшаем DT, а вершину T возвращаем в множество M1, помещая её в начало очереди.

Разумеется, при каждом обновлении массива D следует обновлять и значение в массиве P.

Подробности реализации

Создадим массив ID[1..N], в котором для каждой вершины будем хранить, какому множеству она принадлежит: 0 - если M2 (т.е. расстояние равно бесконечности), 1 - если M1 (т.е. вершина находится в очереди), и 2 - если M0 (некоторый

путь уже был найден, расстояние меньше бесконечности).

Очередь обработки можно реализовать стандартной структурой данных deque. Однако есть более эффективный способ. Во-первых, очевидно, в очереди в любой момент времени будет храниться максимум N элементов. Но, вовторых, мы можем добавлять элементы и в начало, и в конец очереди. Следовательно, мы можем организовать очередь на массиве размера N, однако нужно зациклить его. Т.е. делаем массив Q[1..N], указатели (int) на первый элемент QH и на элемент после последнего QT. Очередь пуста, когда QH == QT. Добавление в конец - просто запись в Q[QT] и увеличение QT на 1; если QT после этого вышел за пределы очереди (QT == N), то делаем QT = 0. Добавление в начало очереди - уменьшаем QH на 1, если она вышла за пределы очереди (QH == -1), то делаем QH = N-1.

Сам алгоритм реализуем в точности по описанию выше.

Асимптотика

Мне не известна более-менее хорошая асимптотическая оценка этого алгоритма. Я встречал только оценку O (N M) у похожего алгоритма.

Однако на практике алгоритма зарекомендовал себя очень хорошо: время его работы я оцениваю как O (M log N), хотя, повторюсь, это исключительно экспериментальная оценка.

Реализация

typedef pair<int,int> rib;

typedef vector < vector<rib> > graph;

const int inf = 1000*1000*1000;

int main()

{

int n, v1, v2; graph g (n);

... чтение графа ...

vector<int> d (n, inf); d[v1] = 0;

vector<int> id (n); deque<int> q; q.push_back (v1); vector<int> p (n, -1);

while (!q.empty())

{

int v = q.front(), q.pop_front(); id[v] = 1;

for (size_t i=0; i<g[v].size(); ++i)

{

int to = g[v][i].first, len = g[v][i].second; if (d[to] > d[v] + len)

{

d[to] = d[v] + len; if (id[to] == 0)

q.push_back (to); else if (id[to] == 1)

q.push_front (to); p[to] = v;

id[to] = 1;

}

}

}

... вывод результата ...

}