Алгоритмы C++

Тернарный поиск

Постановка задачи

Пусть дана функция

, унимодальная на некотором отрезке

. Под унимодальностью понимается один

из двух вариантов. Первый: функция сначала строго возрастает, потом достигает максимума (в одной точке или целом отрезке), потом строго убывает. Второй вариант, симметричный: функция сначала убывает убывает, достигает минимума, возрастает. В дальнейшем мы будем рассматривать первый вариант, второй будет абсолютно симметричен ему.

Требуется найти максимум функции на отрезке .

Алгоритм

Возьмём любые две точки и в этом отрезке: . Посчитаем значения функции и . Дальше у нас получается три варианта:

● Если окажется, что

, то искомый максимум не может находиться в левой части, т.е. в части

.

В этом легко убедиться: если в левой точке функция меньше, чем в правой, то либо эти две точки находятся в области "подъёма" функции, либо только левая точка находится там. В любом случае, это означает, что максимум дальше имеет смысл искать только в отрезке .

● Если, наоборот,

, то ситуация аналогична предыдущей с точностью до симметрии. Теперь

искомый максимум не может находиться в правой части, т.е. в части 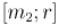, поэтому переходим к отрезку .

● Если , то либо обе эти точки находятся в области максимума, либо левая точка находится в области возрастания, а правая — в области убывания (здесь существенно используется то, что возрастание/

убывание строгие). Таким образом, в дальнейшем поиск имеет смысл производить в отрезке	, но (в
целях упрощения кода) этот случай можно отнести к любому из двух предыдущих.

Таким образом, по результату сравнения значений функции в двух внутренних точках мы вместо текущего отрезка поиска находим новый отрезок . Повторим теперь все действия для этого нового отрезка, снова

получим новый, строго меньший, отрезок, и т.д.

Рано или поздно длина отрезка станет маленькой, меньшей заранее определённой константы-точности, и процесс можно останавливать. Этот метод численный, поэтому после остановки алгоритма можно приближённо считать, что во всех точках отрезка 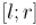достигается максимум; в качестве ответа можно взять, например, точку .

Осталось заметить, что мы не накладывали никаких ограничений на выбор точек и . От этого способа, понятно, будет зависеть скорость сходимости (но и возникающая погрешность). Наиболее распространённый способ

— выбирать точки так, чтобы отрезок делился ими на 3 равные части:

Впрочем, при другом выборе, когда и ближе друг к другу, скорость сходимости несколько увеличится.

Случай целочисленного аргумента

Если аргумент функции целочисленный, то отрезок				тоже становится дискретным, однако, поскольку мы
не накладывали никаких ограничений на выбор точек			и	, то на корректность алгоритма это никак не влияет.
Можно по-прежнему выбирать	и	так, чтобы они делили отрезок			на 3 части, но уже равные
только приблизительно.
Второй отличающийся момент — критерий остановки алгоритма. В данном случае тернарный поиск надо
будет останавливать, когда станет		, ведь в таком случае уже невозможно будет выбрать точки				и
так, чтобы были различными и отличались от и , и это может привести к зацикливанию. После того, как
алгоритм тернарного поиска остановится и станет				, из оставшихся нескольких точек-
кандидатов	надо выбрать точку с максимальным значением функции.

Реализация

Реализация для непрерывного случая (т.е. функция имеет вид: ):

double l = ..., r = ..., EPS = ...; // входные данные while (r - l > EPS) {

double m1 = l + (r - l) / 3, m2 = r - (r - l) / 3;

if (f (m1) < f (m2))

l = m1; else

r = m2;

}

Здесь — фактически, абсолютная погрешность ответа (не считая погрешностей, связанных с неточным вычислением функции).

Вместо критерия "while (r - l > EPS)" можно выбрать и такой критерий останова:

for (int it=0; it<iterations; ++it)

С одной стороны, придётся подобрать константу	, чтобы обеспечить требуемую точность (обычно
достаточно нескольких сотен, чтобы достичь максимальной точности). Но зато, с другой стороны, число
итераций перестаёт зависеть от абсолютных величин и	, т.е. мы фактически с помощью

задаём требуемую относительную погрешность.

Биномиальные коэффициенты

Биномиальным коэффициентом

называется количество способов выбрать набор предметов из

различных предметов без учёта порядка расположения этих элементов (т.е. количество неупорядоченных наборов). Также биномиальные коэффициенты - это коффициенты в разложении (т.н. бином Ньютона):

Считается, что эту формулу, как и треугольник, позволяющий эффективно находить коэффициенты, открыл Блез Паскаль (Blaise Pascal), живший в 17 в. Тем не менее, она была известна ещё китайскому математику Яну Хуэю (Yang Hui), жившему в 13 в. Возможно, её открыл персидский учёный Омар Хайям (Omar Khayyam). Более того,

индийский математик Пингала (Pingala), живший ещё в 3 в. до н.э., получил близкие результаты. Заслуга же Ньютона заключается в том, что он обобщил эту формулу для степеней, не являющихся натуральными.

Вычисление

Аналитическая формула для вычисления:

Эту формулу легко вывести из задачи о неупорядоченной выборке (количество способов неупорядоченно выбрать элементов из элементов). Сначала посчитаем количество упорядоченных выборок. Выбрать первый элемент есть

способов, второй —	, третий —	, и так далее. В результате для числа упорядоченных выборок
получаем формулу:		. К неупорядоченным выборкам легко
перейти, если заметить, что каждой неупорядоченной выборке соответствует ровно			упорядоченных (т.к. это
количество всевозможных перестановок		элементов). В результате, деля	на , мы и получаем

искомую формулу.

Рекуррентная формула (с которой связан знаменитый "треугольник Паскаля"):

Её легко вывести через предыдущую формулу.

Стоит заметить особо, при значение всегда полагается равным нулю.

Свойства

Биномиальные коэффициенты обладают множеством различных свойств, приведём наиболее простые из них:

●Правило симметрии:

●Внесение-вынесение:

●Суммирование по :

●Суммирование по :

●Суммирование по и :

● Суммирование квадратов:

●Взвешенное суммирование:

●Cвязь с числами Фибоначчи:

Вычисления в программе

Непосредственные вычисления по аналитической формуле

Вычисления по первой, непосредственной формуле, очень легко программировать, однако этот способ подвержен переполнениям даже при сравнительно небольших значениях и (даже если ответ вполне помещается в какой-нибудь тип данных, вычисление промежуточных факториалов может привести к переполнению). Поэтому очень часто этот способ можно применять только вместе с [[Длинная арифметика|Длинной арифметикой]]:

int C (int n, int k) { int res = 1;

for (int i=n-k+1; i<=n; ++i) res *= i;

for (int i=2; i<=k; ++i) res /= i;

}

Улучшенная реализация

Можно заметить, что в приведённой выше реализации в числителе и знаменателе стоит одинаковое количество сомножителей ( ), каждый из которых не меньше единицы. Поэтому можно заменить нашу дробь на произведение дробей, каждая из которых является вещественнозначной. Однако, можно заметить, что после домножения текущего ответа на каждую очередную дробь всё равно будет получаться целое число (это, например, следует из свойства "внесения-вынесения"). Таким образом, получаем такую реализацию:

int C (int n, int k) { double res = 1;

for (int i=1; i<=k; ++i)

res = res * (n-k+i) / i; return (int) (res + 0.01);

}

Здесь мы аккуратно приводим дробное число к целому, учитывая, что из-за накапливающихся погрешностей оно может оказаться чуть меньше истинного значения (например, вместо трёх).

Треугольник Паскаля

С использованием же рекуррентного соотношения можно построить таблицу биномиальных коэффициентов (фактически, треугольник Паскаля), и из неё брать результат. Преимущество этого метода в том, что промежуточные результаты никогда не превосходят ответа, и для вычисления каждого нового элемента таблицы надо всего лишь одно сложение. Недостатком является медленная работа для больших N и K, если на самом

деле таблица не нужна, а нужно единственное значение (потому что для вычисления

понадобится строить

таблицу для всех , или хотя бы до ).

const int maxn = ...;

int C[maxn+1][maxn+1];

for (int n=0; n<=maxn; ++n) { C[n][0] = C[n][n] = 1;

for (int k=1; k<n; ++k)

C[n][k] = C[n-1][k-1] + C[n-1][k];

}

Если вся таблица значений не нужна, то, как нетрудно заметить, достаточно хранить от неё только две строки (текущую

— -ую строку и предыдущую — -ую).

Вычисление за O(1)

Наконец, в некоторых ситуациях оказывается выгодно предпосчитать заранее значения всех факториалов, с тем, чтобы впоследствии считать любой необходимый биномиальный коэффициент, производя лишь два деления. Это может быть выгодно при использовании Длинной арифметики, когда память не позволяет предпосчитать весь

треугольник Паскаля, или же когда требуется производить расчёты по некоторому простому модулю (если модуль не простой, то возникают сложности при делении числителя дроби на знаменатель; их можно преодолеть, если факторизовать модуль и хранить все числа в виде векторов из степеней этих простых; см раздел

"Длинная арифметика в факторизованном виде").

Числа Каталана

Числа Каталана — числовая последовательность, встречающаяся в удивительном числе комбинаторных задач.

Эта последовательность названа в честь бельгийского математика Каталана (Catalan), жившего в 19 веке, хотя на самом деле она была известна ещё Эйлеру (Euler), жившему за век до Каталана.

Последовательность

Первые несколько чисел Каталана (начиная с нулевого):

Числа Каталана встречаются в большом количестве задач комбинаторики. -ое число Каталана — это:

●	Количество корректных скобочных последовательностей, состоящих из открывающих и закрывающих скобок.
●	Количество корневых бинарных деревьев с		листьями (вершины не пронумерованы).
●	Количество способов полностью разделить скобками			множитель.
●	Количество триангуляций выпуклого		-угольника (т.е. количество разбиений многоугольника
	непересекающимися диагоналями на треугольники).
●	Количество способов соединить	точек на окружности		непересекающимися хордами.
●	Количество неизоморфных полных бинарных деревьев с внутренними вершинами (т.е. имеющими хотя бы одного сына).
●	Количество монотонных путей из точки		в точку	в квадратной решётке размером		,
	не поднимающихся над главной диагональю.
●	Количество перестановок длины , которые можно отсортировать стеком (можно показать, что перестановка
	является сортируемой стеком тогда и только тогда, когда нет таких индексов				, что	).

● Количество непрерывных разбиений множества из элементов (т.е. разбиений на непрерывные блоки).

● Количество способов покрыть лесенку с помощью прямоугольников (имеется в виду фигура, состоящая из

столбцов, -ый из которых имеет высоту ).

Вычисление

Имеется две формулы для чисел Каталана: рекуррентная и аналитическая. Поскольку мы считаем, что все приведённые выше задачи эквивалентны, то для доказательства формул мы будем выбирать ту задачу, с помощью которой это сделать проще всего.

Рекуррентная формула

Рекуррентную формулу легко вывести из задачи о правильных скобочных последовательностях.

Самой левой открывающей скобке l соответствует определённая закрывающая скобка r, которая разбивает формулу две части, каждая из которых в свою очередь является правильной скобочной последовательностью. Поэтому, если мы обозначим , то для любого фиксированного будет ровно способов. Суммируя это

по всем допустимым , мы и получаем рекуррентную зависимость на .

Аналитическая формула

(здесь через обозначен, как обычно, биномиальный коэффициент).

Эту формулу проще всего вывести из задачи о монотонных путях. Общее количество монотонных путей в решётке размером равно . Теперь посчитаем количество монотонных путей, пересекающих

диагональ. Рассмотрим какой-либо из таких путей, и найдём первое ребро, которое стоит выше диагонали. Отразим относительно диагонали весь путь, идущий после этого ребра. В результате получим монотонный путь в

решётке

. Но, с другой стороны, любой монотонный путь в решётке

обязательно пересекает диагональ, следовательно, он получен как раз таким способом из

какого-либо (причём единственного) монотонного пути, пересекающего диагональ, в решётке . Монотонных путей в решётке имеется . В результате получаем формулу:

Ожерелья

Задача "ожерелья" — это одна из классических комбинаторных задач. Требуется посчитать количество различных ожерелий из 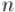бусинок, каждая из которых может быть покрашена в один из цветов. При сравнении двух ожерелий их можно поворачивать, но не переворачивать (т.е. разрешается сделать циклический сдвиг).

Решение

Решить эту задачу можно, используя лемму Бернсайда и теорему Пойа. [ Ниже идёт копия текста из этой статьи ]

В этой задаче мы можем сразу найти группу инвариантных перестановок. Очевидно, она будет состоять из перестановок:

Найдём явную формулу для вычисления				. Во-первых, заметим, что перестановки имеют такой вид, что в -
ой перестановке на -ой позиции стоит				(взятое по модулю	, если оно больше ). Если мы будем
рассматривать циклическую структуру -ой перестановки, то увидим, что единица переходит в						,	переходит
в	,	— в	, и т.д., пока не придём в число		; для остальных элементов выполняются
похожие утверждения. Отсюда можно понять, что все циклы имеют одинаковую длину, равную							, т.
е.		("gcd" — наибольший общий делитель, "lcm" — наименьшее общее кратное). Тогда количество циклов

в -ой перестановке будет равно просто .

Подставляя найденные значения в теорему Пойа, получаем решение:

Можно оставить формулу в таком виде, а можно её свернуть ещё больше. Перейдём от суммы по всем к сумме только по делителям . Действительно, в нашей сумме будет много одинаковых слагаемых: если не является делителем ,