Алгоритмы C++

Количество помеченных графов

Дано число	вершин. Требуется посчитать количество	различных помеченных графов с		вершинами (т.
е. вершины графа помечены различными числами от до		, и графы сравниваются с учётом этой покраски
вершин). Рёбра графа неориентированы, петли и кратные рёбра запрещены.
Рассмотрим множество всех возможных рёбер графа. Для любого ребра			положим, что	(основываясь

на неориентированности графа и отсутствии петель). Тогда множество всех возможных рёбер графа имеет мощность

, т.е. .

Поскольку любой помеченный граф однозначно определяется своими рёбрами, то количество помеченных графов с вершинами равно:

Количество связных помеченных графов

По сравнению с предыдущей задачей мы дополнительно накладываем ограничение, что граф должен быть связным. Обозначим искомое число через .

Научимся, наоборот, считать количество несвязных графов; тогда количество связных графов получится как минус найденное число. Более того, научимся считать количество корневых (т.е. с выделенной вершиной

- корнем) несвязных графов; тогда количество несвязных графов будет получаться из него делением на

. Заметим, что, так как граф несвязный, то в нём найдётся компонента связности, внутри которой лежит корень, а остальной граф будет представлять собой ещё несколько (как минимум одну) компонент связности.

Переберём количество	вершин в этой компоненте связности, содержащей корень (очевидно,					),
и найдём количество таких графов. Во-первых, мы должны выбрать				вершин из , т.е. ответ умножается на		.
Во-вторых, компонента связности с корнем даёт множитель				. В-третьих, оставшийся граф из
вершин является произвольным графом, а потому он даёт множитель				. Наконец, количество способов
выделить корень в компоненте связности из		вершин равно	. Итого, при фиксированном		количество
корневых несвязных графов равно:

Значит, количество несвязных графов с вершинами равно:

Наконец, искомое количество связных графов равно:

Количество помеченных графов с компонентами связности

Основываясь на предыдущей формуле, научимся считать количество помеченных графов с			вершинами и
компонентами связности.
Сделать это можно с помощью динамического программирования. Научимся считать			—
количество помеченных графов с	вершинами и	компонентами связности.
Научимся вычислять очередной элемент		, зная предыдущие значения. Воспользуемся стандартным

приёмом при решении таких задач: возьмём вершину с номером 1, она принадлежит какой-то компоненте, вот эту компоненту мы и будем перебирать. Переберём размер этой компоненты, тогда количество способов выбрать

такое множество вершин равно	(одну вершину — вершину 1 — перебирать не надо). Количество же
способов построить компоненту связности из		вершин мы уже умеем считать — это		. После удаления
этой компоненты из графа у нас остаётся граф с		вершинами и	компонентами связности, т.е.
мы получили рекуррентную зависимость, по которой можно вычислять значения				:

Итого получаем примерно такой код:

int d[n+1][k+1]; // изначально заполнен нулями d[0][0][0] = 1;

for (int i=1; i<=n; ++i)

for (int j=1; j<=i && j<=k; ++j) for (int s=1; s<=i; ++s)

d[i][j] += C[i-1][s-1] * conn[s] * d[i-s][j-1]; cout << d[n][k][n];

Разумеется, на практике, скорее всего, нужна будет длинная арифметика.

Генерация сочетаний из N элементов

Сочетания из N элементов по K в лексикографическом порядке

Постановка задачи. Даны натуральные числа N и K. Рассмотрим множество чисел от 1 до N. Требуется вывести все различные его подмножества мощности K, причём в лексикографическом порядке.

Алгоритм весьма прост. Первым сочетанием, очевидно, будет сочетание (1,2,...,K). Научимся для текущего сочетания находить лексикографически следующее. Для этого в текущем сочетании найдём самый правый элемент, не достигший ещё своего наибольшего значения; тогда увеличим его на единицу, а всем последующим элементам присвоим наименьшие значения.

bool next_combination (vector<int> & a, int n) { int k = (int)a.size();

for (int i=k-1; i>=0; --i) if (a[i] < n-k+i+1) {

++a[i];

for (int j=i+1; j<k; ++j) a[j] = a[j-1]+1;

return true;

}

return false;

}

С точки зрения производительности, этот алгоритм линеен (в среднем), если K не близко к N (т.е. если не выполняется, что K = N - o(N)). Для этого достаточно доказать, что сравнения "a[i] < n-k+i+1" выполняются в сумме Cn+1k раз, т.е. в (N

+1) / (N-K+1) раз больше, чем всего есть сочетаний из N элементов по K.

Сочетания из N элементов по K с изменениями ровно одного элемента

Требуется выписать все сочетания из N элементов по K, но в таком порядке, что любые два соседних сочетания будут отличаться ровно одним элементом.

Интуитивно можно сразу заметить, что эта задача похожа на задачу генерации всех подмножеств данного множества

в таком порядке, когда два соседних подмножества отличаются ровно одним элементом. Эта задача непосредственно решается с помощью Кода Грея: если мы каждому подмножеству поставим в соответствие

битовую маску, то, генерируя с помощью кодов Грея эти битовые маски, мы и получим ответ.

Может показаться удивительным, но задача генерации сочетаний также непосредственно решается с помощью кода Грея. А именно, сгенерируем коды Грея для чисел от 0 до 2N-1, и оставим только те коды, которые содержат ровно K единиц. Удивительный факт заключается в том, что в полученной последовательности любые две соседние маски (а также первая и последняя маски) будут отличаться ровно двумя битами, что нам как раз и требуется.

Докажем это.

Для доказательства вспомним факт, что последовательность G(N) кодов Грея можно получить следующим образом:

G(N) = 0G(N-1) 1G(N-1)R

т.е. берём последовательность кодов Грея для N-1, дописываем в начало каждой маски 0, добавляем к ответу; затем снова берём последовательность кодов Грея для N-1, инвертируем её, дописываем в начало каждой маски 1 и добавляем к ответу.

Теперь мы можем произвести доказательство.

Сначала докажем, что первая и последняя маски будут отличаться ровно в двух битах. Для этого достаточно заметить, что первая маска будет иметь вид N-K нулей и K единиц, а последняя маска будет иметь вид: единица, потом N-K-1 нулей, потом K-1 единица. Доказать это легко по индукции по N, пользуясь приведённой выше формулой

для последовательности кодов Грея.

Теперь докажем, что любые два соседних кода будут отличаться ровно в двух битах. Для этого снова обратимся к формуле для последовательности кодов Грея. Пусть внутри каждой из половинок (образованных из G(N-1))

утверждение верно, докажем, что оно верно для всей последовательности. Для этого достаточно доказать, что оно верно в месте "склеивания" двух половинок G(N-1), а это легко показать, основываясь на том, что мы знаем первый и последний элементы этих половинок.

Приведём теперь наивную реализацию, работающую за 2N:

int gray_code (int n) { return n ^ (n >> 1);

}

int count_bits (int n) { int res = 0;

for (; n; n>>=1)

res += n & 1; return res;

}

void all_combinations (int n, int k) { for (int i=0; i<(1<<n); ++i) {

int cur = gray_code (i);

if (count_bits (cur) == k) { for (int j=0; j<n; ++j)

if (cur & (1<<j))

printf ("%d ", j+1);

puts ("");

}

}

}

Стоит заметить, что возможна и в некотором смысле более эффективная реализация, которая будет строить всевозможные сочетания на ходу, и тем самым работать за O (Cnk n). С другой стороны, эта

реализация представляет собой рекурсивную функцию, и поэтому для небольших n, вероятно, она имеет большую скрытую константу, чем предыдущее решение.

Собственно сама реализация - это непосредственное следование формуле:

G(N,K) = 0G(N-1,K) 1G(N-1,K-1)R

Эта формула легко получается из приведённой выше формулы для последовательности Грея - мы просто выбираем подпоследовательность из подходящих нам элементов.

bool ans[MAXN];

void gen (int n, int k, int l, int r, bool rev) { if (k > n || k < 0) return;

if (!n) {

for (int i=0; i<n; ++i)

printf ("%d", (int)ans[i]); puts ("");

return;

}

ans[rev?r:l] = false;

gen (n-1, k, !rev?l+1:l, !rev?r:r-1, rev); ans[rev?r:l] = true;

gen (n-1, k-1, !rev?l+1:l, !rev?r:r-1, !rev);

}

void all_combinations (int n, int k) { gen (n, k, 0, n-1, false);

}

Лемма Бернсайда. Теорема Пойа

Лемма Бернсайда

Эта лемма была сформулирована и доказана Бернсайдом (Burnside) в 1897 г., однако было установлено, что эта формула была ранее открыта Фробениусом (Frobenius) в 1887 г., а ещё раньше - Коши (Cauchy) в 1845 г. Поэтому эта формула иногда называется леммой Бернсайда, а иногда - теоремой Коши-Фробениуса.

Лемма Бернсайда позволяет посчитать количество классов эквивалентности в некотором множестве, основываясь на некоторой его внутренней симметрии.

Объекты и представления

Проведём чёткую грань между количеством объектов и количеством представлений.

Одним и тем же объектам могут соответствовать различные представления, но, разумеется, любое представление соответствует ровно одному объекту. Следовательно, множество всех представлений разбивается на классы эквивалентности. Наша задача — в подсчёте именно числа объектов, или, что то же самое, количества классов эквивалентности.

Пример задачи: раскраска бинарных деревьев

Допустим, мы рассматриваем следующую задачу. Требуется посчитать количество способов раскрасить корневые бинарные деревья с вершинами в 2 цвета, если у каждой вершины мы не различаем правого и левого сына.

Множество объектов здесь — это множество различных в этом понимании раскрасок деревьев.

Определим теперь множество представлений. Каждой раскраске поставим в соответствие задающую её функцию

, где	, а	. Тогда множество представлений — это множество различных
функций такого вида, и размер его, очевидно, равен			. В то же время, на этом множестве представлений мы
ввели разбиение на классы эквивалентности.
Например, пусть	, а дерево таково: корень — вершина 1, а вершины 2 и 3 — её сыновья. Тогда
следующие функции	и	считаются эквивалентными:

Инвариантные перестановки

Почему эти две функции и принадлежат одному классу эквивалентности? Интуитивно это понятно — потому что мы можем переставить местами сыновей вершины 1, т.е. вершины 2 и 3, а после такого преобразования функции и совпадут. Но формально это означает, что найдётся такая инвариантная перестановка (т.е. которая

по условию задачи не меняет сам объект, а только его представление), такая, что:

Итак, исходя из условия задачи, мы можем найти все инвариантные перестановки, т.е. применяя которые мы не				и
не переходим из одного класса эквивалентности в другой. Тогда, чтобы проверить, являются ли две функции
эквивалентными (т.е. соответствуют ли они на самом деле одному объекту), надо для каждой
инвариантной перестановки проверить, не выполнится ли условие:	(или, что то же самое,
). Если хотя бы для одной перестановки обнаружилось это равенство, то		и	эквивалентны, иначе они
не эквивалентны.

Нахождение всех таких инвариантных перестановок, относительно которых наша задача инвариантна — это ключевой шаг для применения как леммы Бернсайда, так и теоремы Пойа. Понятно, что эти инвариантные перестановки зависят от конкретной задачи, и их нахождение — процесс чисто эвристический, основанный на интуитивных соображениях. Впрочем, в большинстве случаев достаточно вручную найти несколько "основных" перестановок, из которых все остальные перестановки могут быть получены их всевозможными произведениями (и эту, исключительно механическую, часть работы можно переложить на компьютер; более подробно это будет рассмотрено ниже на примере конкретной задачи).

Нетрудно понять, что инвариантные перестановки образуют группу — поскольку произведение любых инвариантных перестановок тоже является инвариантной перестановкой. Обозначим группу инвариантных перестановок через .

Формулировка леммы

Для формулировки осталось напомнить одно понятие из алгебры. Неподвижной точкой	для перестановки
называется такой элемент, который инвариантен относительно этой перестановки:	. Например, в

нашем примере неподвижными точками будут являться те функции , которые соответствуют раскраскам, не меняющимся при применении к ним перестановки 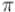(не меняющимся именно в формальном смысле равенства

двух функций). Обозначим через количество неподвижных точек для перестановки .

Тогда лемма Бернсайда звучит следующим образом: количество классов эквивалетности равно сумме количеств неподвижных точек по всем перестановкам из группы , делённой на размер этой группы:

Хотя лемма Бернсайда сама по себе не так удобна для применения на практике (пока непонятно, как быстро искать величину ), она наиболее ясно раскрывает математическую суть, на которой основана идея подсчёта

классов эквивалентности.

Доказательство леммы Бернсайда

Описанное здесь доказательство леммы Бернсайда не так важно для её понимания и применения на практике, поэтому его можно пропустить при первом чтении.

Приведённое здесь доказательство является самым простым из известных и не использует теорию групп. Это доказательство было опубликовано Богартом (Bogart) и Кеннетом (Kenneth) в 1991 г.

Итак, нам нужно доказать следующее утверждение:

Величина, стоящая справа — это не что иное, как количество "инвариантных пар"	, т.е. таких пар, что

. Очевидно, что в формуле мы имеем право изменить порядок суммирования - сделать внешнюю сумму

по элементам f, а внутри неё поставить величину — количество перестановок, относительно которых f инвариантна:

Для доказательства этой формулы составим таблицу, столбцы которой будут подписаны всеми значениями , строки

— всеми перестановками , а в клетках таблицы будут стоять произведения . Тогда, если мы будем

рассматривать столбцы этой таблицы как множества, то некоторые из них могут совпасть, и это будет как означать, что соответствующие этим столбцам также эквивалентны. Таким образом, количество различных как

множество столбцов равно искомой величине	. Кстати говоря, с точки зрения теории групп
столбец таблицы, подписанный некоторым элементом	— это орбита этого элемента; для эквивалентных