Алгоритмы C++
.pdf
элементов, очевидно, орбиты совпадают, и число различных орбит даёт именно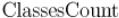 
.
Итак, столбцы таблицы сами распадаются на классы эквивалентности; зафиксируем теперь какой-либо класс
и рассмотрим столбцы в нём. Во-первых, заметим, что в этих столбцах могут стоять только элементы |
одного |
||
класса эквивалентности (иначе получилось бы, что некоторым эквивалентным преобразованием |
мы перешли в |
||
другой класс эквивалентности, что невозможно). Во-вторых, каждый элемент |
будет встречаться одинаковое число |
||
раз во всех столбцах (это также следует из того, что столбцы соответствуют эквивалентным элементам). Отсюда можно сделать вывод, что все столбцы внутри одного класса эквивалентности совпадают друг с другом как мультимножества.
Теперь зафиксируем произвольный элемент . С одной стороны, он встречается в своём столбце ровно |
раз |
(по самому определению ). С другой стороны, все столбцы внутри одного класса эквивалентности одинаковы
как мультимножества. Следовательно, внутри каждого столбца данного класса эквивалентности любой элемент
встречается ровно 
раз.
Таким образом, если мы возьмём произвольным образом от каждого класса эквивалентности по одному столбцу
и просуммируем количество элементов в них, то получим, с одной стороны, |
(это получается, |
просто умножив количество столбцов на их размер), а с другой стороны — сумму величин |
по всем (это |
следует из всех предыдущих рассуждений): |
|
|
|
|
|
что и требовалось доказать.
Теорема Пойа. Простейший вариант
Теорема Пойа (Polya) является обобщением леммы Бернсайда, к тому же предоставляющая более удобный инструмент для нахождения количества классов эквивалентности. Следует отметить, что ещё до Пойа эта теорема была открыта и доказана Редфилдом (Redfield) в 1927 г., однако его публикация прошла незамеченной математиками того времени. Пойа независимо пришёл к тому же результату лишь в 1937 г., и его публикация была более удачной.
Здесь мы рассмотрим формулу, получающуюся как частный случай теоремы Пойа, и которую очень удобно использовать для вычислений на практике. Общая теорема Пойа в данной статье рассматриваться не будет.
Обозначим через |
количество циклов в перестановке . Тогда выполняется следующая формула |
(частный случай теоремы Пойа):
|
|
|
где — количество значений, которые может принимать каждый элемент представления |
. Например, в |
|
нашей задаче-примере (раскраска корневого бинарного дерева в 2 цвета) |
. |
|
Доказательство
Эта формула является прямым следствием леммы Бернсайда. Чтобы получить её, нам надо просто найти явное выражение для величины , фигурирующую в лемме (напомним, это количество неподвижных
точек перестановки 
).
Итак, рассмотрим некоторую перестановку и некоторый элемент |
. Под действием перестановки элементы |
передвигаются, как известно, по циклам перестановки. Заметим, |
что так как в результате должно получаться |
, то внутри каждого цикла перестановки должны находиться одинаковые элементы . В то же время, для
разных циклов никакой связи между значениями элементов не возникает. Таким образом, для каждого цикла перестановки 
мы выбираем по одному значению (среди вариантов), и тем самым мы получим все представления
, инвариантные относительно этой перестановки, т.е.:
где 
— количество циклов перестановки.
Пример задачи: Ожерелья
Задача "ожерелья" — это одна из классических комбинаторных задач. Требуется посчитать количество различных ожерелий из 
бусинок, каждая из которых может быть покрашена в один из цветов. При сравнении двух ожерелий их можно поворачивать, но не переворачивать (т.е. разрешается сделать циклический сдвиг).
В этой задаче мы можем сразу найти группу инвариантных перестановок. Очевидно, она будет состоять из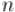 
перестановок:
-ой перестановке будет равно просто 
.
учтётся несколько раз, т.е. сумму можно представить в таком виде:
, и окончательно получаем 
для ручных вычислений, и вычислить аналитически количество циклов в них не представляется возможным.
В таком случае следует вручную найти несколько "основных" перестановок, которых будет достаточно для порождения всей группы . Далее можно написать программу, которая сгенерирует все перестановки группы 
, посчитает в каждой из них количество циклов и подставит их в формулу.
Рассмотрим для примера задачу о количестве раскрасок тора. Имеется прямоугольный клетчатый лист
бумаги |
, некоторые из клеток покрашены в чёрный цвет. Затем из этого листа получают |
цилиндр, склеивая две стороны с длинами 
. Затем из цилиндра получают тор, склеивая две окружности (базы цилиндра) без перекручивания. Требуется посчитать количество различных торов (лист был изначально
покрашен произвольно), считая, что линии склеивания неразличимы, а тор можно поворачивать и переворачивать.
В данной задаче представлением можно считать лист бумаги , некоторые клетки которого покрашены в чёрный цвет. Нетрудно понять, что следующие виды преобразований сохраняют класс эквивалентности: циклический сдвиг строк листа, циклический сдвиг столбцов листа, поворот листа на 180 градусов; также интуитивно можно понять, что этих трёх видов преобразований достаточно для порождения всей группы инвариантных преобразований. Если мы каким-либо образом занумеруем клетки поля, то мы можем записать три перестановки , , ,
соответствующие этим видам преобразований. Дальше остаётся только сгенерировать все перестановки,
получающиеся как произведения этой. Очевидно, что все такие перестановки имеют вид |
, |
|||
где |
, |
, |
. |
|
Таким образом, мы можем написать реализацию решения этой задачи:
void mult (vector<int> & a, const vector<int> & b) { vector<int> aa (a);
for (size_t i=0; i<a.size(); ++i) a[i] = aa[b[i]];
}
int cnt_cycles (vector<int> a) { int res = 0;
for (size_t i=0; i<a.size(); ++i) if (a[i] != -1) {
++res;
for (size_t j=i; a[j]!=-1; ) { size_t nj = a[j];
a[j] = -1; j = nj;
}
}
return res;
}
int main() { int n, m;
cin >> n >> m;
vector<int> p (n*m), p1 (n*m), p2 (n*m), p3 (n*m); for (int i=0; i<n*m; ++i) {
p[i] = i;
p1[i] = (i % n + 1) % n + i / n * n; p2[i] = (i / n + 1) % m * n + i % n;
p3[i] = (m - 1 - i / n) * n + (n - 1 - i % n);
}
int sum = 0, cnt = 0; set < vector<int> > s;
for (int i1=0; i1<n; ++i1) {
for (int i2=0; i2<m; ++i2) { for (int i3=0; i3<2; ++i3) {
if (!s.count(p)) { s.insert (p); ++cnt;
sum += 1 << cnt_cycles(p);
}
mult (p, p3);
}
mult (p, p2);
}
mult (p, p1);
}
cout << sum / cnt;
}
Игры на произвольных графах
Пусть игра ведётся двумя игроками на некотором графе G. Т.е. текущее состояние игры - это некоторая вершина графа, и из каждой вершины рёбра идут в те вершины, в которые можно пойти следующим ходом.
Мы рассматриваем самый общий случай - случай произвольного ориентированного графа с циклами. Требуется для заданной начальной позиции определить, кто выиграет при оптимальной игре обоих игроков (или определить, что результатом будет ничья).
Мы решим эту задачу очень эффективно - найдём ответы для всех вершин графа за линейное относительно количества рёбер время - O (M).
Описание алгоритма
Про некоторые вершины графа заранее известно, что они являются выигрышными или проигрышными; очевидно, такие вершины не имеют исходящих рёбер.
Имеем следующие факты:
●если из некоторой вершины есть ребро в проигрышную вершину, то эта вершина выигрышная;
●если из некоторой вершины все рёбра исходят в выигрышные вершины, то эта вершина проигрышная;
●если в какой-то момент ещё остались неопределённые вершины, но ни одна из них не подходят ни под первое, ни под второе правило, то все эти вершины - ничейные.
Таким образом, уже ясен алгоритм, работающий за асимптотику O (N M) - мы перебираем все вершины, пытаемся
к каждой применить первое либо второе правило, и если мы произвели какие-то изменения, то повторяем всё заново. Однако этот процесс поиска и обновления можно значительно ускорить, доведя асимптотику до линейной.
Переберём все вершины, про которые изначально известно, что они выигрышные или проигрышные. Из каждой из них пустим следующий поиск в глубину. Этот поиск в глубину будет двигаться по обратным рёбрам. Прежде всего, он не будет заходить в вершины, которые уже определены как выигрышные или проигрышные. Далее, если поиск в глубину пытается пойти из проигрышной вершины в некоторую вершину, то её он помечает как выигрышную, и идёт в неё. Если же поиск в глубину пытается пойти из выигрышной вершины в некоторую вершину, то он должен проверить, все ли рёбра ведут из этой вершины в выигрышные. Эту проверку легко осуществить за O (1), если в каждой вершине будем хранить счётчик рёбер, которые ведут в выигрышные вершины. Итак, если поиск в глубину пытается пойти из выигрышной вершины в некоторую вершину, то он увеличивает в ней счётчик, и если счётчик сравнялся
с количеством рёбер, исходящих из этой вершины, то эта вершина помечается как проигрышная, и поиск в глубину идёт
вэту вершину. Иначе же, если целевая вершина так и не определена как выигрышная или проигрышная, то поиск
вглубину в неё не заходит.
Итого, мы получаем, что каждая выигрышная и каждая проигрышная вершина посещается нашим алгоритмом ровно один раз, а ничейные вершины и вовсе не посещаются. Следовательно, асимптотика действительно O (M).
Реализация
Рассмотрим реализацию поиска в глубину, в предположении, что граф игры построен в памяти, степени исхода посчитаны и записаны в degree (это будет как раз счётчиком, он будет уменьшаться, если есть ребро в выигрышную вершину), а также изначально выигрышные или проигрышные вершины уже помечены.
vector<int> g [100]; bool win [100]; bool loose [100]; bool used[100];
int degree[100];
void dfs (int v) { used[v] = true;
for (vector<int>::iterator i = g[v].begin(); i != g[v].end(); ++i) if (!used[*i]) {
if (loose[v])
win[*i] = true; else if (--degree[*i] == 0)
loose[*i] = true;
else
continue; dfs (*i);
}
}
Пример задачи. "Полицейский и вор"
Чтобы алгоритм стал более ясным, рассмотрим его на конкретном примере.
Условие задачи. Имеется поле размером MxN клеток, в некоторые клетки заходить нельзя. Известны
начальные координаты полицейского и вора. Также на карте может присутствовать выход. Если полицейский окажется в одной клетке с вором, то выиграл полицейский. Если же вор окажется в клетке с выходом (и в этой клетке не стоит полицейский), то выиграет вор. Полицейский может ходить в 8 направлениях, вор - только в 4 (вдоль осей координат). И полицейский, и вор могут пропустить свой ход. Первым ход делает полицейский.
Построение графа. Построим граф игры. Мы должны формализовать правила игры. Текущее состояние игры определяется координатами полицейского P, вора T, а также булева переменная Pstep, которая определяет, кто будет делать следующий ход. Следовательно, вершина графа определена тройкой (P,T,Pstep). Граф построить легко, просто соответствуя условию.
Далее нужно определить, какие вершины являются выигрышными или проигрышными изначально. Здесь есть тонкий момент. Выигрышность/проигрышность вершины помимо координат зависит и от Pstep - чей сейчас ход. Если сейчас ход полицейского, то вершина выигрышная, если координаты полицейского и вора совпадают; вершина проигрышная, если она не выигрышная и вор находится на выходе. Если же сейчас ход вора, то вершина выигрышная, если вор находится на выходе, и проигрышная, если она не выигрышная и координаты полицейского и вора совпадают.
Единственный момент, которой нужно решить - строить граф явно или делать это "на ходу", прямо в поиске в глубину. С одной стороны, если строить граф предварительно, то будет меньше вероятность ошибиться. С
другой стороны, это увеличит объём кода, да и время работы будет в несколько раз медленнее, чем если строить граф "на ходу".
Реализация всей программы:
struct state { char p, t;
bool pstep;
};
vector<state> g [100][100][2];
// 1 = policeman coords; 2 = thief coords; 3 = 1 if policeman's step or 0 if thief's.
bool win [100][100][2]; bool loose [100][100][2]; bool used[100][100][2]; int degree[100][100][2];
void dfs (char p, char t, bool pstep) { used[p][t][pstep] = true;
for (vector<state>::iterator i = g[p][t][pstep].begin(); i != g[p]
[t][pstep].end(); ++i)
if (!used[i->p][i->t][i->pstep]) { if (loose[p][t][pstep])
win[i->p][i->t][i->pstep] = true; else if (--degree[i->p][i->t][i->pstep] == 0)
loose[i->p][i->t][i->pstep] = true;
else
continue;
dfs (i->p, i->t, i->pstep);
}
}
int main() {
int n, m;
cin >> n >> m; vector<string> a (n); for (int i=0; i<n; ++i)
cin >> a[i];
for (int p=0; p<n*m; ++p)
for (int t=0; t<n*m; ++t)
for (char pstep=0; pstep<=1; ++pstep) {
int px = p/m, py = p%m, tx=t/m, ty=t%m;
if (a[px][py]=='*' || a[tx][ty]=='*') continue;
bool & wwin = win[p][t][pstep]; |
|
bool & lloose = loose[p][t][pstep]; |
|
if (pstep) |
lloose |
wwin = px==tx && py==ty, |
|
= !wwin && a[tx][ty] == 'E'; |
|
else |
lloose |
wwin = a[tx][ty] == 'E', |
|
= !wwin && px==tx && py==ty; |
|
if (wwin || lloose) continue; |
|
state st = { p, t, !pstep }; |
|
|
g[p][t][pstep].push_back |
(st); |
|
|
|
st.pstep = pstep |
!= 0; |
|
|
|
degree[p][t][pstep] = 1; |
|
|
|
1, 1 |
const int dx[] = |
{ -1, 0, 1, 0, |
-1, -1, |
|
}; |
{ 0, 1, |
0, -1, |
-1, 1, - |
|
1, 1 |
const int dy[] = |
|||
}; |
|
|
{ |
|
|
for (int d=0; d<(pstep?8:4); ++d) |
|||
int ppx=px, ppy=py, ttx=tx, tty=ty; if (pstep)
ppx += dx[d], ppy += dy[d];
else
ttx += dx[d], tty += dy[d]; if (ppx>=0 && ppx<n && ppy>=0 &&
ppy<m && a[ppx][ppy]!='*' &&
ttx>=0 && ttx<n && tty>=0
&& tty<m && a[ttx][tty]!='*')
{
g[ppx*m+ppy][ttx*m+tty][!
pstep].push_back (st);
++degree[p][t][pstep];
}
}
}
for (int p=0; p<n*m; ++p)
for (int t=0; t<n*m; ++t)
for (char pstep=0; pstep<=1; ++pstep)
if ((win[p][t][pstep] || loose[p][t]
[pstep]) && !used[p][t][pstep])
dfs (p, t, pstep!=0);
int p_st, t_st;
for (int i=0; i<n; ++i)
for (int j=0; j<m; ++j)
if (a[i][j] == 'C') p_st = i*m+j;