
- •12. Ряд Тейлора. Критерий разложимости функции в ряд Тейлора.
- •1. Числовые ряды. Основные понятия. Действия над рядами. Необходимое условие сходимости ряда
- •2. Интегральный признак сходимости рядов с неотрицательными членами
- •3. Признаки сравнения для рядов с неотрицательными членами
- •4. Признак Даламбера для рядов с неотрицательными членами
- •5. Признак Коши для рядов с неотрицательными членами
- •6. Знакочередующиеся ряды. Признак Лейбница
- •7. Знакопеременные ряды, ряды с комплексными членами. Абсолютная и условная сходимость. Свойства абсолютно и условно сходящихся рядов
- •8. Равномерная сходимость функционального ряда. Признак Вейерштрасса равномерной сходимости
- •9. Свойства равномерно сходящихся функциональных рядов: теоремы о непрерывности суммы, о почленном дифференцировании и почленном интегрировании
- •10.1 Степенные ряды. Теорема Абеля. Радиус и интервал (круг) сходимости степенного ряда
- •15.Основные элементарные функции комплексной переменной
- •16. Производная функции комплексной переменной. Условия Коши-Римана. Аналитические функции. Действительная и мнимая части аналитической функции
- •17. Интеграл от функции комплексной переменной, его вычисление и свойства
- •18. Интегральная теорема Коши. Первообразная и интеграл аналитической функции
- •18. Интегральная теорема Коши. Первообразная и интеграл аналитической функции
- •19.Интегральная формула Коши. Теорема о производных аналитической функции
- •20. Ряды в комплексной области. Свойства функциональных рядов. Степенные ряды
- •21. Ряд Тейлора для функции комплексной переменной. Ряд Лорана
- •22. Нули и изолированные особые точки аналитических функций. Классификация изолированных особых точек
- •23. Понятие вычета. Основная теорема о вычетах
- •24. Вычисление вычетов
- •25. Вычисление интегралов вида,с помощью вычетов
- •26. Скалярное произведение функций. Норма функции. Ортогональные системы функций. Основная тригонометрическая система функций
- •27. Ряды Фурье по ортогональным системам функций
- •28. Сходимость в среднем функционального ряда. Связь между различными видами сходимости. Экстремальное свойство коэффициентов ряда Фурье
- •29. Неравенство Бесселя. Равенство Парсеваля-Стеклова. Полнота и замкнутость ортогональной системы функций
- •30. Тригонометрические ряды Фурье для периодических функций. Признак сходимости тригонометрического ряда Фурье (теорема Дирихле)
- •31. Разложение непериодических функций в тригонометрический ряд Фурье. Ряд Фурье только по косинусам или только по синусам
- •32. Комплексная форма тригонометрического ряда Фурье. Понятие о спектре
- •33. Интеграл Фурье. Комплексная форма интеграла Фурье
- •34. Преобразования Фурье. Косинус- и синус- преобразования Фурье
- •35. Преобразование Лапласа, оригинал и изображение. Основные теоремы операционного исчисления
- •36. Приложение операционного метода к решению дифференциальных уравнений и систем дифференциальных уравнений
2. Интегральный признак сходимости рядов с неотрицательными членами
an
∈
R,
 ,
an≥0,
Sn+1=Sn+an+1≥Sn
,(Sn) – неубывающ.
,
an≥0,
Sn+1=Sn+an+1≥Sn
,(Sn) – неубывающ.
(Sn) сх
∃число
М,
Sn≤М,Vn(т.Вейерштрасе)
Теор(Критерий сходимости ряда с неотр. Чл.): Для того, чтобы ряд с неотр. Чл. Сходился необх. И дост., чтобы последовательность его частичных сумм была ограничена.
Инт призн. Сход:
Теор(Коши-Маклорена):Пусть ф-ция f(x):[1;+∞) -> R обл св-ми:
Неотрицательна, т.е f(x)≥0,
Vx∈[1;+∞)Непрерывна на [1;+∞)
Невозрастающ. На [1;+∞), тогда
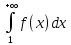 и ряд
и ряд сх или расх одновр,
сх или расх одновр, сх
сх сх
сх
аn+1
≤
 ≤Sn (*) Sn-a1≤
≤Sn (*) Sn-a1≤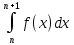 ≤Sn
≤Sn
I.Пусть сх и равенI,
где I-число.
Из
(*) Sn-a1≤a1+
сх и равенI,
где I-число.
Из
(*) Sn-a1≤a1+ ≤ a1+
≤ a1+ +
+ (≥0)
=
(≥0)
= =a1
+I=M,
=a1
+I=M, Vn
(Sn)
– огр, an≥0,
=> по кр. Сх-ти ряда с неотр. Членами.
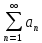 сход.
А
сход.
А схA=>B
схA=>B
В
 сх Ā=>
сх Ā=> т. е. если
ряд расх, то и интегр расх.
т. е. если
ряд расх, то и интегр расх.
II.Пусть
 расх. , тогдаIn+1
=
расх. , тогдаIn+1
=
 неогр.
неогр.
Из (*)
Sn≥In+1= ,
т.е. послед (Sn)также
неогр.
по кр. Сход. Ряда с неотр член.
Ряд
,
т.е. послед (Sn)также
неогр.
по кр. Сход. Ряда с неотр член.
Ряд
 расх.
расх.
 =>
=> ,A=>B,
т. е если
ряд
,A=>B,
т. е если
ряд сх, то и
сх, то и сх
сх
НЕ(B=>A)
 сх, если α>1, расх, еслиα≤1
сх, если α>1, расх, еслиα≤1
 сх,
если α>1, расх, если α≤1
сх,
если α>1, расх, если α≤1
 сх,
если p>1,
расх, если p≤1
сх,
если p>1,
расх, если p≤1
3. Признаки сравнения для рядов с неотрицательными членами
Теор 1. Если
для рядов
 и
и выполн нер-во 0≤an≤bn
для
выполн нер-во 0≤an≤bn
для Vn∈N,
то ряд bn сх =>ряд аn сх или an расх =>bn
Следствие
Если 0≤an≤ bn,где
bn,где
 ∈
R,
∈
R,
 ,
то верно заключение теор 1.
,
то верно заключение теор 1.
Замечание: теор 1. Верна, если 0≤an≤bn начинает выполние с некоторого места.
Теор 2. (предельный
признак сравнения):
Пусть bn>0,
an>0,
для Vn∈N
Пусть ∃
 =c,
тогда:
=c,
тогда:
Если 0<c<+∞, то ряды
 и
и
 сх или расходновременно
сх или расходновременноЕсли с=0, то из того, что
 сх след, что
сх след, что
 сх
схЕсли с=+∞, то из того, что
 сх след, что
сх след, что
 сх,
сх, расх след,
что
расх след,
что расх
расх
Замечание:
С=1 ∃

an=bn
an=bnA)
 ,a≠0,
сх, если α<1, расх, если α≥1
,a≠0,
сх, если α<1, расх, если α≥1
B) сх,
если α>1, расх, если α≤1
сх,
если α>1, расх, если α≤1
 сх,
если p>1, расх, если p≤1
сх,
если p>1, расх, если p≤1
4. Признак Даламбера для рядов с неотрицательными членами
Если ∃
 (
( ,an>0),
то
,an>0),
то
При 0<l<1 ряд
 сх.
сх.l>0 ряд
 расх.
расх.l=1, ничего нельзя сказать
Док-во
 ,
где l-число
,
где l-число
Vɛ>0
∃
N=N(ɛ)
Vn>N(ɛ)
=> | |
< ɛ
|
< ɛ
l - ɛ
< <l+
ɛ
(
l - ɛ)an<an+1<an(l+ɛ)
<l+
ɛ
(
l - ɛ)an<an+1<an(l+ɛ)
0≤l<1
Пусть l+ ɛ<1 α::= l+ ɛ
an+1<αan Vn≥N
 и
и

 =
=
 сх =>
сх => сх
сх
l>1
Пусть ɛ>0, чтобы l-ɛ>0
 >l-
ɛ>1
>l-
ɛ>1
an+1>an,Vn≥N(ɛ),
an≠0=>ряд
расх.
l=1
 расх
расх

 1
1
5. Признак Коши для рядов с неотрицательными членами
Если ∃
 (
( ,an>0),
то
,an>0),
то
При 0<l<1 ряд
 сх.
сх.l>0 ряд
 расх.
расх.l=1, ничего нельзя сказать
Док-во:
 ,
где l-число
,
где l-число
Vɛ>0
∃
N=N(ɛ)
Vn>N(ɛ)
=>
| |
< ɛ
|
< ɛ
l
- ɛ < <l+
ɛ далее
смотри предыдущую теорему
<l+
ɛ далее
смотри предыдущую теорему
Замечания:

n! – ф-ла Стерлинга
– ф-ла Стерлинга
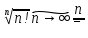
6. Знакочередующиеся ряды. Признак Лейбница
Знакочередующимся наз-ся следующий ряд
an1,-an2,
an3,-(-1)n-1an=
Теор(признак Лейбница) Если an ↓0, т. е.
 =0
=0(an) монотонно убывает (не возраст.)
an≥an+1Vn,
то
 сх, причем
сх, причем
(S-Sn)≤an+1


an=
 ↓0,
↓0,
7. Знакопеременные ряды, ряды с комплексными членами. Абсолютная и условная сходимость. Свойства абсолютно и условно сходящихся рядов
Знакопеременный
ряд – ряд вида
 ,
содержащий как положительные, так и
отрицательные члены.
Пр:1)
1-1+1-1+1-1+1-1+…+(-1)
,
содержащий как положительные, так и
отрицательные члены.
Пр:1)
1-1+1-1+1-1+1-1+…+(-1) +…=
+…=
Т: Если
сходится ряд
 ,то
сходится и ряд
,то
сходится и ряд
Д-во:
 сх =>
сх =>
 сх
сх
0≤an + |an|≤2|an|
 сх <=
сх <= сх
сх
 =
= -
-
Сх <= cx и cx
Ряды с комплексными членами.
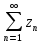 , zn∈C
, zn∈C
Zn = an+i*bn
 cx
cx
 сх
сх
Т: Если
сх ряд
 ,
то сход и ряд
,
то сход и ряд
Д-во:
|zn|
=
 an
≤
an
≤
 =|zn|
bn≤
=|zn|
bn≤
 =|zn|
=|zn|
Дано:
 cx
cx
 сх
сх
↓ ↓

 сх
сх
1 и 2 =>
 cx
cx
 ,
,
 ∈R
или
∈R
или
 ∈C
∈C
О: Если ряд
 cx,
то ряд
cx,
то ряд
 называетсяабсолютно
сходящ.
называетсяабсолютно
сходящ.
Если ряд
 раcx,
а
раcx,
а
 сх, то ряд
сх, то ряд наз.условно
сходящ.
наз.условно
сходящ.


Сх сх абсол.
Расх сх условн
Расх расх
Т. Абсолютно сходящ ряд остается абс. Сход. При любой перестановке его членов, его сумма не изменяется.
Замечание: утверждение теор. справедливо для любого сх-ся знакопостоянного ряда

 ∈R
∈R
Т.(Римана) Если ряд an сход. усл, то какое бы и было наперед заданное число А, можно так переставить члены этого ряда, что сумма будет равна А. Более того, члены условно сх-ся ряда можно переставить так, что преобразованный ряд станет расходящимся.
