
- •12. Ряд Тейлора. Критерий разложимости функции в ряд Тейлора.
- •1. Числовые ряды. Основные понятия. Действия над рядами. Необходимое условие сходимости ряда
- •2. Интегральный признак сходимости рядов с неотрицательными членами
- •3. Признаки сравнения для рядов с неотрицательными членами
- •4. Признак Даламбера для рядов с неотрицательными членами
- •5. Признак Коши для рядов с неотрицательными членами
- •6. Знакочередующиеся ряды. Признак Лейбница
- •7. Знакопеременные ряды, ряды с комплексными членами. Абсолютная и условная сходимость. Свойства абсолютно и условно сходящихся рядов
- •8. Равномерная сходимость функционального ряда. Признак Вейерштрасса равномерной сходимости
- •9. Свойства равномерно сходящихся функциональных рядов: теоремы о непрерывности суммы, о почленном дифференцировании и почленном интегрировании
- •10.1 Степенные ряды. Теорема Абеля. Радиус и интервал (круг) сходимости степенного ряда
- •15.Основные элементарные функции комплексной переменной
- •16. Производная функции комплексной переменной. Условия Коши-Римана. Аналитические функции. Действительная и мнимая части аналитической функции
- •17. Интеграл от функции комплексной переменной, его вычисление и свойства
- •18. Интегральная теорема Коши. Первообразная и интеграл аналитической функции
- •18. Интегральная теорема Коши. Первообразная и интеграл аналитической функции
- •19.Интегральная формула Коши. Теорема о производных аналитической функции
- •20. Ряды в комплексной области. Свойства функциональных рядов. Степенные ряды
- •21. Ряд Тейлора для функции комплексной переменной. Ряд Лорана
- •22. Нули и изолированные особые точки аналитических функций. Классификация изолированных особых точек
- •23. Понятие вычета. Основная теорема о вычетах
- •24. Вычисление вычетов
- •25. Вычисление интегралов вида,с помощью вычетов
- •26. Скалярное произведение функций. Норма функции. Ортогональные системы функций. Основная тригонометрическая система функций
- •27. Ряды Фурье по ортогональным системам функций
- •28. Сходимость в среднем функционального ряда. Связь между различными видами сходимости. Экстремальное свойство коэффициентов ряда Фурье
- •29. Неравенство Бесселя. Равенство Парсеваля-Стеклова. Полнота и замкнутость ортогональной системы функций
- •30. Тригонометрические ряды Фурье для периодических функций. Признак сходимости тригонометрического ряда Фурье (теорема Дирихле)
- •31. Разложение непериодических функций в тригонометрический ряд Фурье. Ряд Фурье только по косинусам или только по синусам
- •32. Комплексная форма тригонометрического ряда Фурье. Понятие о спектре
- •33. Интеграл Фурье. Комплексная форма интеграла Фурье
- •34. Преобразования Фурье. Косинус- и синус- преобразования Фурье
- •35. Преобразование Лапласа, оригинал и изображение. Основные теоремы операционного исчисления
- •36. Приложение операционного метода к решению дифференциальных уравнений и систем дифференциальных уравнений
18. Интегральная теорема Коши. Первообразная и интеграл аналитической функции
Т. Если
f(x)
– аналитическая в односвязной области
D
и ограничена кусочно-гладким контуром
Г и непрерывна в
 ,
то
,
то
Д-во:
f(z)=U(x,y)+V(x,y)*i
f ’(z) – непрерывная ф-ция (доп. предположение ) => /* усл.
U(x,y), V(x,y) имеют непр. частичные произв. 1 порядка. теоремы
Грина
Пусть D - односвязная область, ограниченная кусочно-гладким контуром Г (гамма) */
Теорема Грина.

 Следствие.
Пусть область
D
- не односвязная, ф-ция f(z)
– аналитическая в области D
и непр. в
Следствие.
Пусть область
D
- не односвязная, ф-ция f(z)
– аналитическая в области D
и непр. в
 Граница Г
Граница Г
 ,
где L
– внешний контур
,
где L
– внешний контур
 – внутренние контуры
– внутренние контуры

Д-во:



Первообразная и интеграл аналитической функции
Пусть f(x) – аналитическая ф-ция в односвязной области D
f(z)=U(x,y)+V(x,y)*i

(Р) (Q) (P) (Q)
Усл. нез-ти КРИ-2
от пути:
 всюду в обл.D.
всюду в обл.D.

 –не зав-т от ф-мы
пути
–не зав-т от ф-мы
пути
 (1)
(1)
Теорема Мореры. Пусть f(x) – аналитическая ф-ция в односвязной области D. Тогда ф-ция (1) также анал-кая в области D и вып-ся: Ф' (z)=f(z) (аналог т. Барроу)
Ф(z) – первообразная для f(z) в области D
Ф(z) + С – комплексна константа явл. первообразной для f(z) в области D
Неопределённые
инт-лы
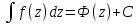
 =
= a,b
–комплексные константы
a,b
–комплексные константы
19.Интегральная формула Коши. Теорема о производных аналитической функции
Т. Пусть
ф-ция f(x)
– аналитическая в односвязной области
D,
ограничена кусочно-гладким контуром Г
и непрерывна в
 ,
тогда для
,
тогда дляV
внутренней
т.
 ∈
D
имеет место интегральная формула Коши:
∈
D
имеет место интегральная формула Коши:
 ,
где к-р Г нах-ся в + напр.
,
где к-р Г нах-ся в + напр.
Д-во:


Замечание. Если обл. D неодносвязна, то интегральная формула Коши имеет место, но под к-м Г понимается сов-ть всех границ
Теорема о производных аналитической функции
Т. Если
ф-ция f(x)
– аналитическая в односвязной области
D,
ограничена кусочно-гладким контуром Г
и непрерывна в
 ,
то тогда для
,
то тогда дляV
внутренней
т.
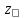 ∈
D
и для
∈
D
и для V
n
∈
N
Ǝ
 , где к-р Г
нах-ся в + напр.
, где к-р Г
нах-ся в + напр.
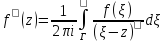 –ИЗОП инт-л
зав-т от параметра (z – пар-р)
–ИЗОП инт-л
зав-т от параметра (z – пар-р)
 z≠ξ
непр. в
z≠ξ
непр. в


ИЗОП можно диф-ть по пар-ру:
 Аналитическая в обл.Dф-ция диф-ма беск. число раз.
Аналитическая в обл.Dф-ция диф-ма беск. число раз.

20. Ряды в комплексной области. Свойства функциональных рядов. Степенные ряды
Числовые ряды






усл. ряд
Функциональные ряды комплексной переменной

 –однозначны
–однозначны

 сх. к f(z),
если Ǝ
сх. к f(z),
если Ǝ

Признак Вейерштрассе дословно повторяется. Определение для действительной области.
1) Если
 непр.
в областиD
при
непр.
в областиD
при V
n
∈
N
2) Если
 сх. равномерно наD
к
сх. равномерно наD
к

 D
D
Т2.
то для V
кусочно-гладкого контура L
∈
D

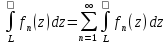
Т3. 1) Если
 аналитична в обл. D
при
аналитична в обл. D
при V
n
∈
N
2)Если
 сх. равномерно на мн-веD
к
сх. равномерно на мн-веD
к
 ,
,
то f(z)
 в обл.D,
а ряд
в обл.D,
а ряд
 можно почленно диф-ть
можно почленно диф-тьV
кол-во раз

V
z
∈
D,
k
∈ N
и каждый из пол-ных рядов сх. равномерно
в обл. D
Степенные ряды в комплексной области
 ,
Cn,
Z,
Z0
– комплексные числа ∈
С
,
Cn,
Z,
Z0
– комплексные числа ∈
С
Из т. Абелля если
Ǝ R
≥= 0 такое, что ряд нах-ся внутри круга
 и расходится вне круга
и расходится вне круга .
. м. б. точки, в кот сходится и расходится.R
– радиус сходимости степенного ряда.
м. б. точки, в кот сходится и расходится.R
– радиус сходимости степенного ряда.


Внутри круга


 мажоранта, действ. знакопол. ряд.
мажоранта, действ. знакопол. ряд.
Сумма степенного
ряда явл. непрерывной, аналитической,
интегрируемой почленно по V
пути, нах-ся внутри круга
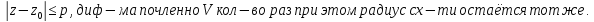
Каждый степенной
ряд явл. рядом Тейлора для своей суммы,
т. е.

