
- •12. Ряд Тейлора. Критерий разложимости функции в ряд Тейлора.
- •1. Числовые ряды. Основные понятия. Действия над рядами. Необходимое условие сходимости ряда
- •2. Интегральный признак сходимости рядов с неотрицательными членами
- •3. Признаки сравнения для рядов с неотрицательными членами
- •4. Признак Даламбера для рядов с неотрицательными членами
- •5. Признак Коши для рядов с неотрицательными членами
- •6. Знакочередующиеся ряды. Признак Лейбница
- •7. Знакопеременные ряды, ряды с комплексными членами. Абсолютная и условная сходимость. Свойства абсолютно и условно сходящихся рядов
- •8. Равномерная сходимость функционального ряда. Признак Вейерштрасса равномерной сходимости
- •9. Свойства равномерно сходящихся функциональных рядов: теоремы о непрерывности суммы, о почленном дифференцировании и почленном интегрировании
- •10.1 Степенные ряды. Теорема Абеля. Радиус и интервал (круг) сходимости степенного ряда
- •15.Основные элементарные функции комплексной переменной
- •16. Производная функции комплексной переменной. Условия Коши-Римана. Аналитические функции. Действительная и мнимая части аналитической функции
- •17. Интеграл от функции комплексной переменной, его вычисление и свойства
- •18. Интегральная теорема Коши. Первообразная и интеграл аналитической функции
- •18. Интегральная теорема Коши. Первообразная и интеграл аналитической функции
- •19.Интегральная формула Коши. Теорема о производных аналитической функции
- •20. Ряды в комплексной области. Свойства функциональных рядов. Степенные ряды
- •21. Ряд Тейлора для функции комплексной переменной. Ряд Лорана
- •22. Нули и изолированные особые точки аналитических функций. Классификация изолированных особых точек
- •23. Понятие вычета. Основная теорема о вычетах
- •24. Вычисление вычетов
- •25. Вычисление интегралов вида,с помощью вычетов
- •26. Скалярное произведение функций. Норма функции. Ортогональные системы функций. Основная тригонометрическая система функций
- •27. Ряды Фурье по ортогональным системам функций
- •28. Сходимость в среднем функционального ряда. Связь между различными видами сходимости. Экстремальное свойство коэффициентов ряда Фурье
- •29. Неравенство Бесселя. Равенство Парсеваля-Стеклова. Полнота и замкнутость ортогональной системы функций
- •30. Тригонометрические ряды Фурье для периодических функций. Признак сходимости тригонометрического ряда Фурье (теорема Дирихле)
- •31. Разложение непериодических функций в тригонометрический ряд Фурье. Ряд Фурье только по косинусам или только по синусам
- •32. Комплексная форма тригонометрического ряда Фурье. Понятие о спектре
- •33. Интеграл Фурье. Комплексная форма интеграла Фурье
- •34. Преобразования Фурье. Косинус- и синус- преобразования Фурье
- •35. Преобразование Лапласа, оригинал и изображение. Основные теоремы операционного исчисления
- •36. Приложение операционного метода к решению дифференциальных уравнений и систем дифференциальных уравнений
32. Комплексная форма тригонометрического ряда Фурье. Понятие о спектре
Пусть
 – периодическая функция T=2l,
– периодическая функция T=2l,

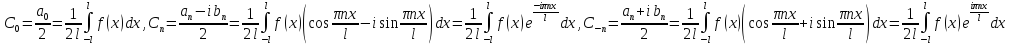

Понятие о спектрах
Функция вида
 .
.
A
– амплитуда, wt
– фаза колебания,
 – начальная фаза,w
– круговая частота
– начальная фаза,w
– круговая частота

Функция вида
 –гармоника,т.к.
–гармоника,т.к.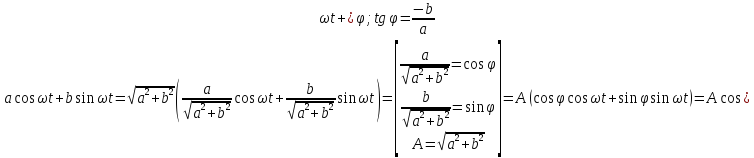


Любой периодический
сигнал T=2l,
удовлетворяющий условиям Дирихле,
представляется в виде такой суммы
 иn-ых
гармоник, характеристики которых
выражаются через коэффициенты ряда
Фурье.
иn-ых
гармоник, характеристики которых
выражаются через коэффициенты ряда
Фурье.
 –называется n-й
комплексной гармоникой.
–называется n-й
комплексной гармоникой.


 –сопряженный;
–сопряженный; ,n=0,1,2…
,n=0,1,2…
О. Последовательность
 – называется амплитудным спектром
сигналаf(t)
с периодом 2l
– называется амплитудным спектром
сигналаf(t)
с периодом 2l
Последовательность
 называется фазовым спектром сигналаf(t)
называется фазовым спектром сигналаf(t)
f(t)=I(t) – сила тока, T=2l, R=1 – сопротивление.
Энергия сигнала
равна работе.
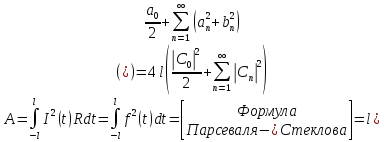 – энергия сигнала
– энергия сигнала
Амплитудный спектр сигнала f(t) несет всю информацию о энергии сигнала и показывает как она … по частотам.
33. Интеграл Фурье. Комплексная форма интеграла Фурье
2l – периодическая функция.
f(x) – непериодическая функция, задана (-∞;+∞)
Считаем f(x) периодической с T=2l+∞
f(x)
– абсолютно интегрируема на (-∞;+∞),т.
е.
 и конечен
и конечен ,
,
L’(-∞;+∞)- класс абсолютно интегрируемых функций.
Пусть f(x)
на каждом конечном отрезке является
кусочно-гладкой, т. е. удовлетворяет
условиям теоремы Дирихле. Выражение
 – называют интегралом Фурье дляf(x);
– называют интегралом Фурье дляf(x);

T
Пусть функция
f(x)
является кусочно-непрерывной и
кусочно-гладкой для любого отрезка [-l;
l]
и абсолютно интегрируемой на (-∞;+∞).
Тогда интеграл Фурье I(x)
сходится в каждой точке
 и справедливо
и справедливо
I(x)=f(x), если x – точка непрерывности функции f(x)
 ,
если x
– точка разрыва 1 рода функции f(xb)
,
если x
– точка разрыва 1 рода функции f(xb)
Замечания:
Если f(x) – четная, то b(w)=0; a(w)=
 ;
;
Если f(x)
– нечетная, то a(w)=0;
b(w)=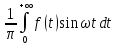 ;
;
f(x) абсолютно интегрируема на
 .
.
Можно продолжить
f(x) на
 ,
либо четным образом, либо нечетным.
,
либо четным образом, либо нечетным.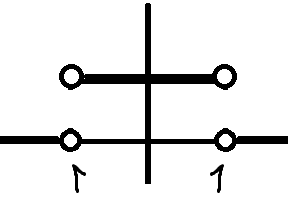

b(w)=0;
a(w)=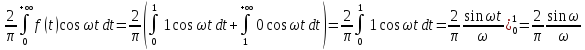

Пусть x=0,
 – Интеграл Дирихле
– Интеграл Дирихле

Интеграл Фурье задает непериодическую функцию суммой бесконечно большого числа гармоник, близких по частоте.

Комплексная форма интеграла Фурье

 (сходится в смысле
(сходится в смысле
 p.)
p.)




 –Комплексная
форма интеграла Фурье
–Комплексная
форма интеграла Фурье
34. Преобразования Фурье. Косинус- и синус- преобразования Фурье
Пусть f(x) L’(-∞;+∞)
– (абсолютно интегрируемая функция)
кусочно-непрерывная и кусочно-гладкая
на любом отрезке [-l,
l],
тогда почти во всех точках f(x):
L’(-∞;+∞)
– (абсолютно интегрируемая функция)
кусочно-непрерывная и кусочно-гладкая
на любом отрезке [-l,
l],
тогда почти во всех точках f(x):

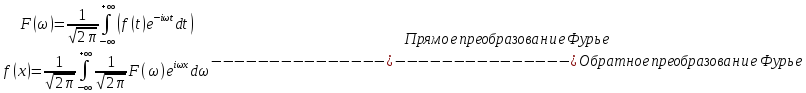
 –спектральная
плотность функции f(x)
;
–спектральная
плотность функции f(x)
;
 - амплитудный спектр;
- амплитудный спектр; – фазовый спектр.
– фазовый спектр.


Пусть f(x)
– нечетная функция
 ,
,




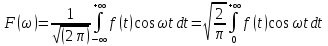
 -
четная функция,
-
четная функция,


 ,
где g(x)
- четная, h(x)
– нечетная
,
где g(x)
- четная, h(x)
– нечетная
 ;
; 
35. Преобразование Лапласа, оригинал и изображение. Основные теоремы операционного исчисления
Операционное исчисление – один из методов математического анализа, позволяющий в ряде случаев сводить исследование дифференциальных и некоторых типов интегральных операторов и решение уравнений, содержащих эти операторы, к рассмотрению более простых алгебраических задач.
Методы операционного исчисления предполагают реализацию следующей условной схемы решения задачи.
От искомых функций переходят к некоторым другим функциям – их изображениям.
Над изображениями производят операции, соответствующие заданным операциям над самими функциями.
Получив некоторый результат при действиях над изображениями возвращаются к самим функциям.
В качестве изображения, позволяющего перейти от функции к их изображениям, будем применять так называемое преобразование Лапласа.
Преобразование Лапласа
Пусть f(t) – действительная функция действительного переменногоt( подtбудем понимать время или координату)
Функция f(t) называетсяоригиналом, если она удовлетворяет следующим условиям:
f(t)
 0
приt<0.
0
приt<0.f(t) – кусочно-непрерывная приt
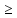 0,
т. е. она непрерывна или имеет точки
разрываIрода, причем на
каждом конечном промежутке осиtтаких точек лишь конечное число.
0,
т. е. она непрерывна или имеет точки
разрываIрода, причем на
каждом конечном промежутке осиtтаких точек лишь конечное число.Существуют такие числа M>0 иs0
 0,
что для всехtвыполняется
неравенство |f(t)
0,
что для всехtвыполняется
неравенство |f(t) ,
т. е. при возрастанииtфункцияf(t)
может возрастать не быстрее некоторой
показательной функции.
,
т. е. при возрастанииtфункцияf(t)
может возрастать не быстрее некоторой
показательной функции.
Условия 1-3 выполняются для большинства функций, описывающих различные физические процессы.
Первое условие означает, что процесс
начинается с какого-то момента времени,
удобнее считать, что в момент t=0.
Третьему условию удовлетворяют
ограниченные функции (для них можно
положитьs0= 0),
степенныеtn
(n>0) и другие ( для
функций видаf(t)
= условие
3 не выполняется). Не является оригиналом,
например, функцияf(t)
=
условие
3 не выполняется). Не является оригиналом,
например, функцияf(t)
= ( не удовлетворяет второму условию).
( не удовлетворяет второму условию).
Замечание: Функция f(t) может быть и комплексной функцией действительного переменного, т.е. иметь видf(t)=f1(t)+if2(t); она считается оригиналом, если действительные функцииf1(t) иf2(t) являются оригиналами.
Изображением оригиналаf(t)
называется функцияF(p)
комплексного переменногоp=s+i ,
определяемая интегралом
,
определяемая интегралом
Операцию перехода от оригинала f(t)
к изображениюF(p)
называютпреобразованием Лапласа.
Соответствие между оригиналомf(t)
и изображениемF(p)
записывается в виде (принято оригиналы обозначать малыми
буквами, а их изображения – соответствующими
большими буквами).
(принято оригиналы обозначать малыми
буквами, а их изображения – соответствующими
большими буквами).
T1 (Существование изображения). Для всякого оригиналаf(t) изображениеF(p) существует (определено) в полуплоскостиRep=s>s0, гдеs0– показатель роста функцииf(t), причем функцияF(p) является аналитической в этой полуплоскости (s>s0)/
Следствие T1.(Необходимый признак существования
изображения). Если функцияF(p)
является изображением функцииf(t)
, то
Т2 (О единственности оригинала). Если функцияF(p) служит изображением двух оригиналовf1(t) иf2(t), то эти оригиналы совпадают друг с другом во всех точках, в которых они непрерывны.
Свойства преобразования Лапласа:Линейность, подобие, смещение, запаздывание.
