
- •12. Ряд Тейлора. Критерий разложимости функции в ряд Тейлора.
- •1. Числовые ряды. Основные понятия. Действия над рядами. Необходимое условие сходимости ряда
- •2. Интегральный признак сходимости рядов с неотрицательными членами
- •3. Признаки сравнения для рядов с неотрицательными членами
- •4. Признак Даламбера для рядов с неотрицательными членами
- •5. Признак Коши для рядов с неотрицательными членами
- •6. Знакочередующиеся ряды. Признак Лейбница
- •7. Знакопеременные ряды, ряды с комплексными членами. Абсолютная и условная сходимость. Свойства абсолютно и условно сходящихся рядов
- •8. Равномерная сходимость функционального ряда. Признак Вейерштрасса равномерной сходимости
- •9. Свойства равномерно сходящихся функциональных рядов: теоремы о непрерывности суммы, о почленном дифференцировании и почленном интегрировании
- •10.1 Степенные ряды. Теорема Абеля. Радиус и интервал (круг) сходимости степенного ряда
- •15.Основные элементарные функции комплексной переменной
- •16. Производная функции комплексной переменной. Условия Коши-Римана. Аналитические функции. Действительная и мнимая части аналитической функции
- •17. Интеграл от функции комплексной переменной, его вычисление и свойства
- •18. Интегральная теорема Коши. Первообразная и интеграл аналитической функции
- •18. Интегральная теорема Коши. Первообразная и интеграл аналитической функции
- •19.Интегральная формула Коши. Теорема о производных аналитической функции
- •20. Ряды в комплексной области. Свойства функциональных рядов. Степенные ряды
- •21. Ряд Тейлора для функции комплексной переменной. Ряд Лорана
- •22. Нули и изолированные особые точки аналитических функций. Классификация изолированных особых точек
- •23. Понятие вычета. Основная теорема о вычетах
- •24. Вычисление вычетов
- •25. Вычисление интегралов вида,с помощью вычетов
- •26. Скалярное произведение функций. Норма функции. Ортогональные системы функций. Основная тригонометрическая система функций
- •27. Ряды Фурье по ортогональным системам функций
- •28. Сходимость в среднем функционального ряда. Связь между различными видами сходимости. Экстремальное свойство коэффициентов ряда Фурье
- •29. Неравенство Бесселя. Равенство Парсеваля-Стеклова. Полнота и замкнутость ортогональной системы функций
- •30. Тригонометрические ряды Фурье для периодических функций. Признак сходимости тригонометрического ряда Фурье (теорема Дирихле)
- •31. Разложение непериодических функций в тригонометрический ряд Фурье. Ряд Фурье только по косинусам или только по синусам
- •32. Комплексная форма тригонометрического ряда Фурье. Понятие о спектре
- •33. Интеграл Фурье. Комплексная форма интеграла Фурье
- •34. Преобразования Фурье. Косинус- и синус- преобразования Фурье
- •35. Преобразование Лапласа, оригинал и изображение. Основные теоремы операционного исчисления
- •36. Приложение операционного метода к решению дифференциальных уравнений и систем дифференциальных уравнений
21. Ряд Тейлора для функции комплексной переменной. Ряд Лорана
Т. Пусть
ф-ция f(z)
аналитическая в круге
 ,
тогда в этом круге ф-цияf(z)
разлагается в степенной ряд
,
тогда в этом круге ф-цияf(z)
разлагается в степенной ряд

 ,
кот. явл. рядом Тэйлора для ф-цииf(z),
т. е.
,
кот. явл. рядом Тэйлора для ф-цииf(z),
т. е. ,
Гр. =
,
Гр. = окр.
окр.
Ряд Тэйлора
 +
+
Все известные разложения ф-ции в ряд Маклорена здесь тоже подойдут.
Ряд Лорана
О. рядом
Лорана с центром в т.
 наз-ся ряд
наз-ся ряд

 { главная часть } {
правильная часть }
{ главная часть } {
правильная часть }
 ,
z,
,
z,
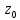 ∈
C
∈
C
 –обл. сх-ти для
прав. Части
–обл. сх-ти для
прав. Части
 =
=

 -
радиус сх-ти; |t|<
-
радиус сх-ти; |t|<

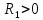
Если r < R , то мн-во сх-ти ряда Лорана
 -
кольцо
-
кольцоЕсли r > R , то обл. сх-ти -
 .
.Если r = R , то доп. иссл-ния
Если r=0, но гл. часть присутствует, z≠
 ,
то
,
то надо выколоть.
надо выколоть.Если r=0 и гл. часть отс-ет, то обл. сх-ти – круг

 ,
сх-ть
равномерная, сумма сх-ти ряда явл.
Аналитической в открытом кольце => ряд
Лорана можно инт-ть по
,
сх-ть
равномерная, сумма сх-ти ряда явл.
Аналитической в открытом кольце => ряд
Лорана можно инт-ть по V
пути, расп-му в кольце и диф-ть почленно.
Т. Ф-ция
f(z)
аналитическая в кольце
 однозначно представима в этом кольце
сход-ся рядом Лорана
однозначно представима в этом кольце
сход-ся рядом Лорана


 Гр – окр-ть
Гр – окр-ть


Замечания.
f(z) не явл-ся анал-кой внутри круга

Ряд Тейлора – частный случай ряда Лорана, когда ф-ция f(z) нал-кая внутри круга
Границы кольца можно раздвинуть до ближайших особых точек ф-ции f(z)
Разложение в ряд
Лорана единственное => найденное V
сп-м разложение аналит. ф-ции п + или –
степеням выр-ния
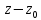 явл.
Лорановским разложением этой ф-ции.
явл.
Лорановским разложением этой ф-ции.
22. Нули и изолированные особые точки аналитических функций. Классификация изолированных особых точек
О. т.
 наз-сянулём
к-го порядка
аналитической ф-ции f(z),
если
наз-сянулём
к-го порядка
аналитической ф-ции f(z),
если
 ,
но
,
но
 .
.
Если
 - ноль к-го порядка, то в разложении ряда
Лорана данной ф-ции
- ноль к-го порядка, то в разложении ряда
Лорана данной ф-ции в окр.
в окр. будет
прис-ть только правильная часть, причём
наим. степень сов-ет с пор. нуля.
будет
прис-ть только правильная часть, причём
наим. степень сов-ет с пор. нуля.

О. т.
 наз-сяизолированной
особой точкой
f(z),
если Ǝ окр.
наз-сяизолированной
особой точкой
f(z),
если Ǝ окр.
 ,
в кот.f(z)
не явл. аналитической. Речь идёт об
однозначных ф-ях f(z).
,
в кот.f(z)
не явл. аналитической. Речь идёт об
однозначных ф-ях f(z).
f(z)
аналитическая в кольце
 .f(z)
можно разложить в этом кольце в
сх-ся
к ней ряд Лорана.
.f(z)
можно разложить в этом кольце в
сх-ся
к ней ряд Лорана.
Ряд Лорана не сод-т гл. части
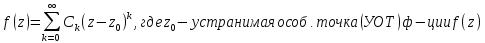
Ряд Лорана сод-т конечное число слагаемых

 ,
{ главная часть }
{ правильная часть }
,
{ главная часть }
{ правильная часть }
 .
Порядок – наим. ст. в знам. гл. части
.
Порядок – наим. ст. в знам. гл. части
Ряд Лорана сод-т бесконечное число слагаемых в гл. части

 .
.
Т1. Для того, чтобы
т.
 являлась УОТ аналитической ф-ции
являлась УОТ аналитической ф-ции ,
необходимо и достаточно, чтобы Ǝ
,
необходимо и достаточно, чтобы Ǝ
Т2. Для того, чтобы
т.
 являлась полюсом аналитической ф-ции
являлась полюсом аналитической ф-ции ,
необходимо и достаточно, чтобы Ǝ
,
необходимо и достаточно, чтобы Ǝ
Т3. Для того, чтобы
т.
 являлась полюсом порядкаm
аналитической ф-ции
являлась полюсом порядкаm
аналитической ф-ции
 ,
необходимо и достаточно, чтобы ф-цию
,
необходимо и достаточно, чтобы ф-цию можно было представить в виде
можно было представить в виде
 ,
где
,
где
 (
( )
–аналитическая ф-ция в т.
)
–аналитическая ф-ция в т. и
и ≠0
≠0

 ;f(z)
;f(z) *
*
Т4. Пусть
 – ИОТ ф-ции
– ИОТ ф-ции

Пусть
 – ноль k-го
порядка для ф-ции
– ноль k-го
порядка для ф-ции
 и нольl-го
порядка для ф-ции
и нольl-го
порядка для ф-ции
 .
Тогда приl>k
т.
.
Тогда приl>k
т.
 явл. полюсом порядкаm=l-kаналитической ф-цииf(z).
явл. полюсом порядкаm=l-kаналитической ф-цииf(z).
T5.Для
того, чтобы т.
 являлась СОТ ф-ции
являлась СОТ ф-ции ,
необходимо и достаточно, чтобы при
,
необходимо и достаточно, чтобы при не имела предела ни конечного, ни
бесконечного. Не сущ
не имела предела ни конечного, ни
бесконечного. Не сущ
23. Понятие вычета. Основная теорема о вычетах
Определение: вычитом ф-ции f(z) в т. Z0 называется число : 1/2πiʃf(z)dz , где Г+ - достаточно малая окружность пробегаемая в положительном направлении
Разложим функцию f(z) в кольцо 0 < Z – Z0 < δ в ряд Лорана:
f(Z)
= … + C-2/(Z
– Z0)^2
+ C-1/(Z
– Z0)
+ C0
+ C1(Z
– Z0)
+ C2(Z
– Z0)^2
+ …
Cn = 1/2πi ʄ (f(ξ) / (ξ - Z0)^(n+1) )*d ξ – интеграл по замкнутому контуру Г( - кольцо)
| Z – Z0| = p
C-1 = 1/2πi ʄ (f(ξ) d ξ
Вычит функции f(z) = коэфициенту C-1 в разложении в ряд Лорано:
res f(z) = C-1 = 1/2πi ʄ (f(ξ) d ξ
Основная теорема о вычитах
Пусть f(z) аналитическая
в области Д за исключением конечного
числа точек Z1,
Z2,
…, Zm
содержащихся в Д и ф-ция непрервна в
обл. Д \ { Z1,
Z2,
…, Zm}
U
L
, где L+
- граница обл. Д пробегаемая в положительном
направлении. Тогда интеграл:
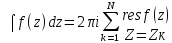
Замечание.
Основная теорема о вычитах справедлива,
когда обл. Д не односвязана.
L = L1 U L2
