
- •12. Ряд Тейлора. Критерий разложимости функции в ряд Тейлора.
- •1. Числовые ряды. Основные понятия. Действия над рядами. Необходимое условие сходимости ряда
- •2. Интегральный признак сходимости рядов с неотрицательными членами
- •3. Признаки сравнения для рядов с неотрицательными членами
- •4. Признак Даламбера для рядов с неотрицательными членами
- •5. Признак Коши для рядов с неотрицательными членами
- •6. Знакочередующиеся ряды. Признак Лейбница
- •7. Знакопеременные ряды, ряды с комплексными членами. Абсолютная и условная сходимость. Свойства абсолютно и условно сходящихся рядов
- •8. Равномерная сходимость функционального ряда. Признак Вейерштрасса равномерной сходимости
- •9. Свойства равномерно сходящихся функциональных рядов: теоремы о непрерывности суммы, о почленном дифференцировании и почленном интегрировании
- •10.1 Степенные ряды. Теорема Абеля. Радиус и интервал (круг) сходимости степенного ряда
- •15.Основные элементарные функции комплексной переменной
- •16. Производная функции комплексной переменной. Условия Коши-Римана. Аналитические функции. Действительная и мнимая части аналитической функции
- •17. Интеграл от функции комплексной переменной, его вычисление и свойства
- •18. Интегральная теорема Коши. Первообразная и интеграл аналитической функции
- •18. Интегральная теорема Коши. Первообразная и интеграл аналитической функции
- •19.Интегральная формула Коши. Теорема о производных аналитической функции
- •20. Ряды в комплексной области. Свойства функциональных рядов. Степенные ряды
- •21. Ряд Тейлора для функции комплексной переменной. Ряд Лорана
- •22. Нули и изолированные особые точки аналитических функций. Классификация изолированных особых точек
- •23. Понятие вычета. Основная теорема о вычетах
- •24. Вычисление вычетов
- •25. Вычисление интегралов вида,с помощью вычетов
- •26. Скалярное произведение функций. Норма функции. Ортогональные системы функций. Основная тригонометрическая система функций
- •27. Ряды Фурье по ортогональным системам функций
- •28. Сходимость в среднем функционального ряда. Связь между различными видами сходимости. Экстремальное свойство коэффициентов ряда Фурье
- •29. Неравенство Бесселя. Равенство Парсеваля-Стеклова. Полнота и замкнутость ортогональной системы функций
- •30. Тригонометрические ряды Фурье для периодических функций. Признак сходимости тригонометрического ряда Фурье (теорема Дирихле)
- •31. Разложение непериодических функций в тригонометрический ряд Фурье. Ряд Фурье только по косинусам или только по синусам
- •32. Комплексная форма тригонометрического ряда Фурье. Понятие о спектре
- •33. Интеграл Фурье. Комплексная форма интеграла Фурье
- •34. Преобразования Фурье. Косинус- и синус- преобразования Фурье
- •35. Преобразование Лапласа, оригинал и изображение. Основные теоремы операционного исчисления
- •36. Приложение операционного метода к решению дифференциальных уравнений и систем дифференциальных уравнений
15.Основные элементарные функции комплексной переменной
Линейные:

Степенные:
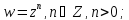
Многочлен:

Дробнорацинальные:

Функция:

Показательная:

Логарифмическая функция:
 ,
,
Тригонометрическая функция:
 ,
в комплексной плоскости не ограничены
,
в комплексной плоскости не ограничены
Гиперболическая функция:

Обратные тригонометрические и гиперболические функции:


Обратные гиперболические:

Общая показательная функция:
 .
.
16. Производная функции комплексной переменной. Условия Коши-Римана. Аналитические функции. Действительная и мнимая части аналитической функции
Производной функции
 называется число
называется число ,
если предел
,
если предел .
.
Функция
 называется дифференц-й в т.
называется дифференц-й в т. ,
если её приращение
,
если её приращение может быть представлено
может быть представлено
 ,A
–комплексная константа.
,A
–комплексная константа.
Теорема. Для того,
чтобы функция
 была дифференцируемой в
была дифференцируемой в ,
необходимо и достаточно, чтобы она имела
производную
,
необходимо и достаточно, чтобы она имела
производную ,
причём
,
причём
Следствие.
 .
Если
.
Если ,
дифференцируема в т.
,
дифференцируема в т. ,
то
,
то
Все основные правила дифференцирования действительных функций сохраняются и для комплексных функций.

Условия Коши-Римана.
Пара функций
 называются удовлетворяющими условиям
Коши-Римана в т.
называются удовлетворяющими условиям
Коши-Римана в т. если в этой точке выполняется следующие
условия:
если в этой точке выполняется следующие
условия:


Теорема. Для того,
чтобы в т. имела производную необходимо, а если
ф-ии
имела производную необходимо, а если
ф-ии дифференцируемы, то и достаточно, чтобы
в точке (х,у) функции
дифференцируемы, то и достаточно, чтобы
в точке (х,у) функции удовлетворяли условиям Коши-Римана.
При этом если производная существует,
то
удовлетворяли условиям Коши-Римана.
При этом если производная существует,
то
Однозначная функция
 называется аналитической в т
называется аналитической в т ,
если
,
если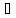 такая открытая окрестность
такая открытая окрестность в каждой точке которой
в каждой точке которой
Функция называется аналитической в области D, если она аналитична в каждой точке этой области.
Действительная и
мнимая части аналитической функции.
Пусть
 аналитична в областиD,
причём
аналитична в областиD,
причём
 имеют непрерывные частные производные
2-го порядка. Выполняется условие
Коши-Римана.
имеют непрерывные частные производные
2-го порядка. Выполняется условие
Коши-Римана.



Функция, удовлетворяющая условию Лапласа – гармоническая
Действительные и мнимые части аналитической функции является гармоническими функциями.
Гармонические функции u и v удовлетворяющие в области D условиям Коши-Римана называются сопряжёнными.
Зная одну из сопряжённых частей гармонической функции и исп-я условия Коши-Римана, можно восстановить гармоническую функцию с точностью до констант, D – односвязная область.
17. Интеграл от функции комплексной переменной, его вычисление и свойства
Пусть в области
 определена однозначная и непрерывная
функция
определена однозначная и непрерывная
функция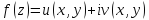

Если
 ,
не зависящей от выбора точек
,
не зависящей от выбора точек и способа разбиения дуги на
и способа разбиения дуги на ,
то он называется интегралом функцииf(z)
на кривой l
с заданной ориентацией.
,
то он называется интегралом функцииf(z)
на кривой l
с заданной ориентацией.

Свойства интеграла от функции комплексной переменной
Линейность:

Аддитивность:




18. Интегральная теорема Коши. Первообразная и интеграл аналитической функции
Теорема. Если
функция
 аналитическая в односвязной областиD,
ограниченной кусочно-гладким контуром
Г и непрерывной в
аналитическая в односвязной областиD,
ограниченной кусочно-гладким контуром
Г и непрерывной в
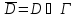 ,
то
,
то .
.
Доказательство:
 –непрерывна. Из
условия теоремы Грина
–непрерывна. Из
условия теоремы Грина
 ,
, имеют непр-ые частные производные 1-го
порядка. Дано, что обл.D
– односвязная, огр. Кусочно-гладким
контуром Г.
имеют непр-ые частные производные 1-го
порядка. Дано, что обл.D
– односвязная, огр. Кусочно-гладким
контуром Г.
 ,
,
 .чтд.
.чтд.
Следствие. Пусть
D
– неоднозначная функция
 – аналитическая в областиD,непрерывна
в
– аналитическая в областиD,непрерывна
в
 .
Граница
.
Граница – внешний контур,
– внешний контур, – внутренние контуры
– внутренние контуры
Первообразная и интеграл аналитической функции.
Пусть
 – аналитическая функция в односвязной
областиD,
– аналитическая функция в односвязной
областиD,

 не зависит от формы
пути.
не зависит от формы
пути.
Теорема Мореры.
Пусть ф-я
 аналитическая
в односвязной областиD,
тогда ф-я
аналитическая
в односвязной областиD,
тогда ф-я
 ,
так же аналитическая в той же области
,
так же аналитическая в той же области – первообразная для
– первообразная для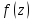 в той же области.
в той же области. ,
где С – такая константа, тоже явл-ся
первообразной дляf(z)
в области D.
,
где С – такая константа, тоже явл-ся
первообразной дляf(z)
в области D.
Интегральная формула Коши
Теорема. Пусть ф-я
 – аналитическая в односвязной областиD,
огр. Кусочно-гладким контуром Г и
непрерывной в
– аналитическая в односвязной областиD,
огр. Кусочно-гладким контуром Г и
непрерывной в
 ,
тогда для любой внешней точки
,
тогда для любой внешней точки имеет место интегральная формула
имеет место интегральная формула
 ,
где контур Г обходится в положительном
направлении.
,
где контур Г обходится в положительном
направлении.
